Lerpで作るアニメーション(easing)を解析する

UIのトランジションなどでよくある実装として、一次補間を用いたものがあります。

この各Buttonはeasingとして一次補間を利用しています。実装が容易なので僕もよく使うのですが、今回はこれの性質を数学的に追求してみましょう。

実装

Unityの場合ですと Mathf.Lerp という関数があります。
p という値にX座標が入っているとして、移動目標のX座標を T とすると、

sample.cs

p = Mathf.Lerp(p, T, 0.1f);

Lerpの引数に自身のpを入れているのがポイント。これだけで次の値をゲットでき、上のような動きを作れます。0.1f を変更すると、どのぐらい急に移動するかを調整できます。（大きいほど急に動く。経験上、どんな状況でもまず0.1を入れておいて様子を見るのがいいです）

一般項

なぜ一般項？

先ほどの実装は、数学的に言えば「漸化式」と呼ばれるものでした。ほとんどの場合これで問題はないのですが、
・任意の時刻の状態を得たい
・逆再生したい
のような状況では漸化式での対応が難しくなります。一般項ならそういったことも解決できるわけです。

Lerp

Mathf.LerpのLerpはLinear Interpolationの略で、ようするに線形補間です。
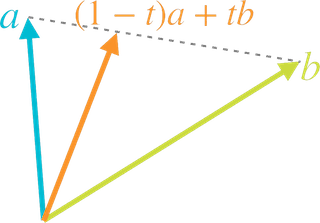
$a$ と $b$ をパラメータ$t$で線形補間すると
$result=(1-t)a + tb$
となり、$t$が０〜１の間で変化すれば結果は$a$と$b$の間に収まるよね、という話ですね。Mathf.Lerpの中ではこんな計算が行われています。
これはベクトルでも成立し、こんな図を高校で習っていると思います。

この式は頻繁に利用する、暗記したほうが良い式ですね。「$t=0$のときは$a$に一致し、$t=1$のときは$b$に一致する」と覚えておけば、思い出すのは難しくないでしょう。ちなみに実装する場合は
$result=(1-t)a+tb=a-ta+tb=(b-a)t+a$
という具合に変形しておくのがセオリーです。（ペナルティなく乗算をひとつ減らせる）

漸化式

では上のプログラムを漸化式に置き換えてみます。

$p_{n}$:nフレーム後の位置
$T$:目標位置
$\alpha$:移動率（プログラムでは0.1fが入っていた）

として、さきほどの線形補間の式より、次のフレームの値 $p_{n+1}$は

$p_{n+1}=(1-\alpha)p_{n}+\alpha T$ ・・・(1)

こうなります。
（なお初期位置、つまり初項$p_{0}$は　$p_{0}=0$ としておきましょう。もし最初の位置がゼロ以外だったら、目標位置$T$にオフセットを加えれば済むので）

一般項を求める

漸化式から一般項を求めます。数列の一般項を求めるテクニックがあり、

$p_{n+1}=(1-\alpha)p_{n}+\alpha T$・・・(1)

この式とよく似た

$s=(1-\alpha)s+\alpha T$・・・(2)

が成立するsを定めます。これが数列の受験テクニック。
(1)-(2)より

$p_{n+1}-s=(p_{n}-s)(1-\alpha)$

$q_{n}=p_{n}-s$とすると

$q_{n+1}=q_{n}(1-\alpha)$

これは等比数列なので一般項が出せます。

$q_{0}=p_{0}-s=-s$より

$q_{n}=-s(1-\alpha)^n$
$p_{n}=q_{n}+s=s-s(1-\alpha)^n=s\left[ 1-(1-\alpha)^n \right] $

式(2)を解けば$s=T$となるので

$p_{n}=T\left[ 1-(1-\alpha)^n \right] $・・・(3)

はい、解けました。受験数学に取り組んだことがある方は懐かしさを覚えるのではないでしょうか。

フレームレートで一般化する

一般項がわかりましたが、実際に利用するにはもうひと工夫が必要です。
そもそもの Lerp の動作に $\Delta t$（デルタティー）が含まれていないため、このままでは実時間ベースのアプリケーションへの応用が難しいのです。

項$n$はフレームに対応しますが、これを時間で一般化しましょう。ここで、元々の動作が60fpsであったとする仮定が必要になります。60回で1秒に相当することにするので、時間$t$について、

$n=60t$

とすれば、$t$を秒とすることができます。よって式(3)を時間$t$の関数にできて、

$f(t)=T\left[ 1-(1-\alpha)^{60 t} \right] $・・・(4)

これが任意の時刻における位置の一般式になります。べき乗はMathf.Powなどで算出できるので、$t$は任意の実数で成り立ちます。つまり120fpsにしても動きは変わりませんし、逆再生も可能になりました。やったね。

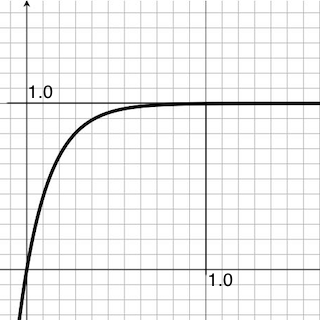
そのままグラフにするとこうなります。実装例は

sample2.cs

float x = (target - m_InitialX) * (1f - Mathf.Pow(1f - 0.1f, 60f * (Time.time - m_StartTime))) + m_InitialX;

こんな感じ。時間を与えると位置が出せる式になっています。

フレームレートを一般化したLerp

まだ続きがあります。
easingでLerpが有用なのは、開始位置を保存しておく必要がない点にもありました。先ほどのプログラムを再掲します。

sample.cs

p = Mathf.Lerp(p, T, 0.1f);

マウスの位置に物体を引き寄せる処理を Lerp で作ってみましょう。

上の例のように移動中に目標位置が変化する場合、一般項だと開始位置が式の中に含まれているので、毎回計算式を作り直すことになってしまいます。これでは一般項の利便性を享受できません。インタラクティブなアプリケーションの場合はこんなふうに、一般項が有利でないケースが多いですね。

Lerpの係数を一般化する

通常のLerpを使用したアニメーションが60fpsで動作しているとしましょう。これが30fpsでも同じアニメーションを再生して欲しいとしたら、Lerpの係数はいくつであれば良いか。これが命題となります。

(3)式
$p_{n}=T\left[ 1-(1-\alpha)^n \right] $

より、例えば60フレーム後の状態は

$p_{60}=T\left[ 1-(1-\alpha)^{60} \right] $

これが30フレーム後の $p_{30}$ に一致する係数を $\alpha$ の代わりに $\beta$ として、

$T\left[ 1-(1-\alpha)^{60} \right] = T\left[ 1-(1-\beta)^{30} \right] $

すなわち

$(1-\alpha)^{60} = (1-\beta)^{30} $

が成立する $\beta$ を求めれば良いことになります。60と30の関係は一般化できるので、60を基準 $n$ 、30を新規の変数 $m$ として、

$(1-\alpha)^{n} = (1-\beta)^{m} $

そして$m$を$n$の比で表すことにして

$m=kn$

とすれば

$(1-\alpha)^{n} = (1-\beta)^{kn} $

これを解いて

$ \beta = 1- (1- \alpha)^{\frac{1}{k}} $

これが求める $\beta$ となります。先に一般項を出しておいたのでスムーズに計算できました。

実装例

60fpsで調整したアニメーションを30fpsにした場合のLerp実行例です。

var ratio30 = 1f - Mathf.Pow(1f - ratio, 60f/30f);
pos = Vector3.Lerp(pos, m_Target, raito30);

ただし$\frac{60}{30}=2$なので、Powを使うまでもなく二乗で構いませんが。
次に、不定フレームレートの場合です。30で割る代わりにTime.deltaTimeを掛けます。

var ratio = 1f - Mathf.Pow(1f - ratio, 60f*Time.deltaTime);
pos = Vector3.Lerp(pos, m_Target, raito);

これでどんなフレームレートでも（フレームレートが高い場合でも）同じ動きをするはずです。

一般項の性質を調べる

話は一般項に戻ります。せっかく一般項が出たので、性質も調べてみましょう。それが可能なのが一般項の良さです。
例えば
「目標に1秒で到達するには、移動率$\alpha$はいくつ以上であればいいんだろう？」
なんて、有用な情報になりそうです。これを調べてみましょう。

指定時刻で到達するための移動率

実は、指定時刻で到達する条件というのは導出不能です。なぜなら、数式上は永遠に目標の値に到達しませんから。
ここは$\epsilon$（イプシロン）を小さな値として「目的地までの距離が$\epsilon$以下になる」という条件にしましょう。
式(4)に $t=1$（1秒）を入れて、

$T\left[ 1-(1-\alpha)^{60} \right] > (1-\epsilon)T$

これを解いて

$\alpha > 1-\epsilon^{\frac{1}{60}}$

これが条件になります。
例えば、仮に$\epsilon=0.01$（すなわち1%）とするなら

$\alpha > 0.073881271871207$

つまり0.08ぐらいの率を入れておけば、1秒後には1%未満のところまで進んでいる、ということが数学的に保証できます。もちろんこれは Mathf.Lerp で実装した場合も成立します。

まとめ

長々と書きましたが、Lerpの係数を一般化したところがハイライトでしょうか。Math.Powを許容すれば実装もシンプルです。
また、一般項を出してしまえば性質が数学的に明らかになるので、完全に制御が可能になる良さがあります。任意のフレームの位置を確定できるので、タイムライン(Unityの機能)と連携するのも容易になるんじゃないでしょうか。補間の性質を把握しておけば、共同作業でも正確な議論や意思の伝達が可能になりますよね。
Lerpを使いながら係数を一般化することもできたので、例えば「あるデバイスだけ120fpsで動作する」といった状況は普通にあり得ると思いますが、今回の結果を用いれば同じ動きのまま滑らかにすることができます。
めでたしめでたし。