最初にコード全体
import cmath
_2pi = 2 * cmath.pi
ROCK = 1
SCISSORS = complex(cmath.cos(_2pi/3), cmath.sin(_2pi/3))
PAPER = complex(cmath.cos(-_2pi/3), cmath.sin(-_2pi/3))
def judge(one, another):
arg = cmath.phase(another / one)
if arg == 0:
return "あいこ"
elif arg > 0:
return "勝ち"
else:
return "負け"
テストコード
def test():
assert "勝ち" == judge(ROCK, SCISSORS)
assert "勝ち" == judge(SCISSORS, PAPER)
assert "勝ち" == judge(PAPER, ROCK)
assert "負け" == judge(SCISSORS, ROCK)
assert "負け" == judge(PAPER, SCISSORS)
assert "負け" == judge(ROCK, PAPER)
assert "あいこ" == judge(ROCK, ROCK)
assert "あいこ" == judge(SCISSORS, SCISSORS)
assert "あいこ" == judge(PAPER, PAPER)
解説
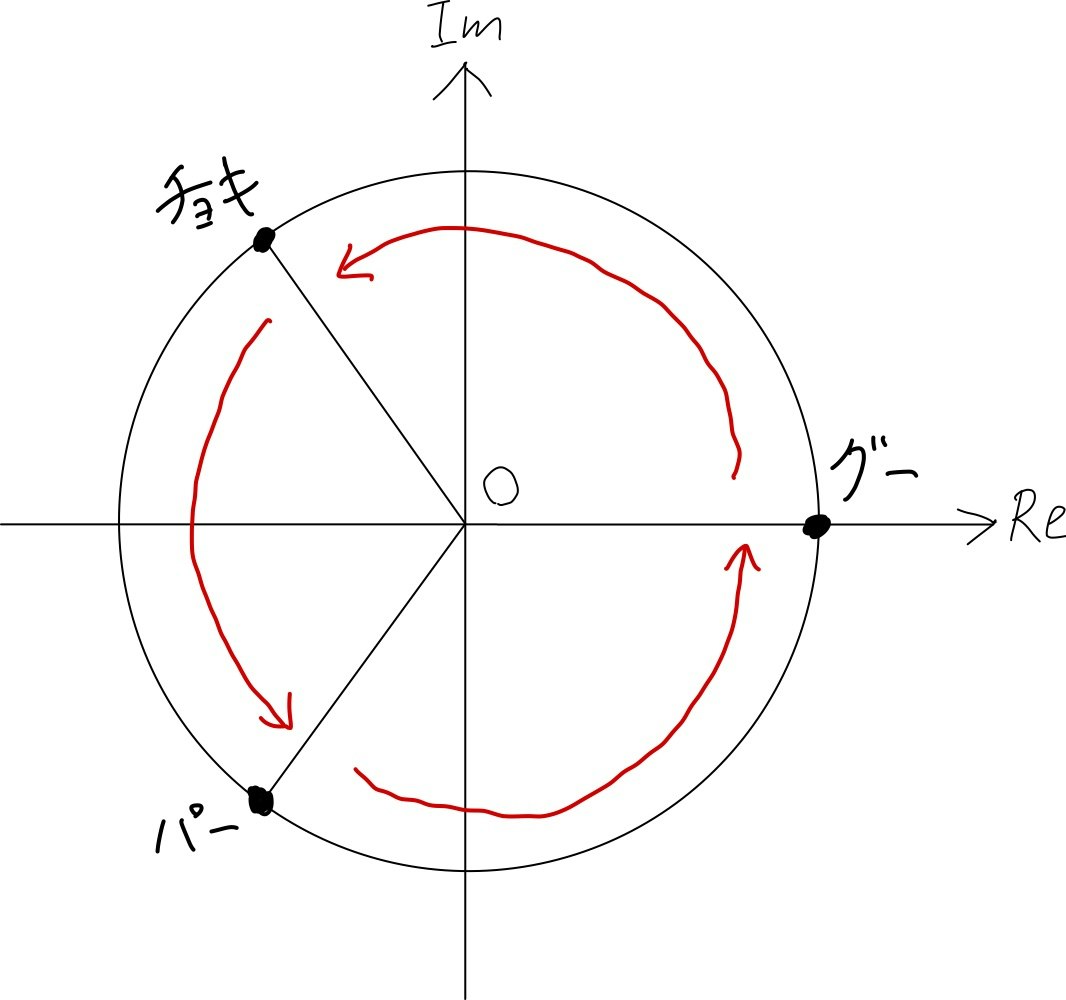
そもそも複素数を導入したモチベは、円上に✊✌✋を配置すれば三つ巴の強弱関係をうまいこと表現できるのではと思ったからである。
complex型(複素数)で定義しているROCK, SCISSORS , PAPER(それぞれ ✊, ✌, ✋)を複素平面上に図示すると下図のようになる。
\begin{align}
\text{ROCK} &= 1 \\
\text{SCISSORS} &= \cos\left( \frac{2\pi}{3} \right) + i \sin\left( \frac{2\pi}{3} \right) \\
\text{PAPER} &= \cos\left( -\frac{2\pi}{3} \right) + i \sin\left( -\frac{2\pi}{3} \right)
\end{align}
| 勝ち | 負け |
 |
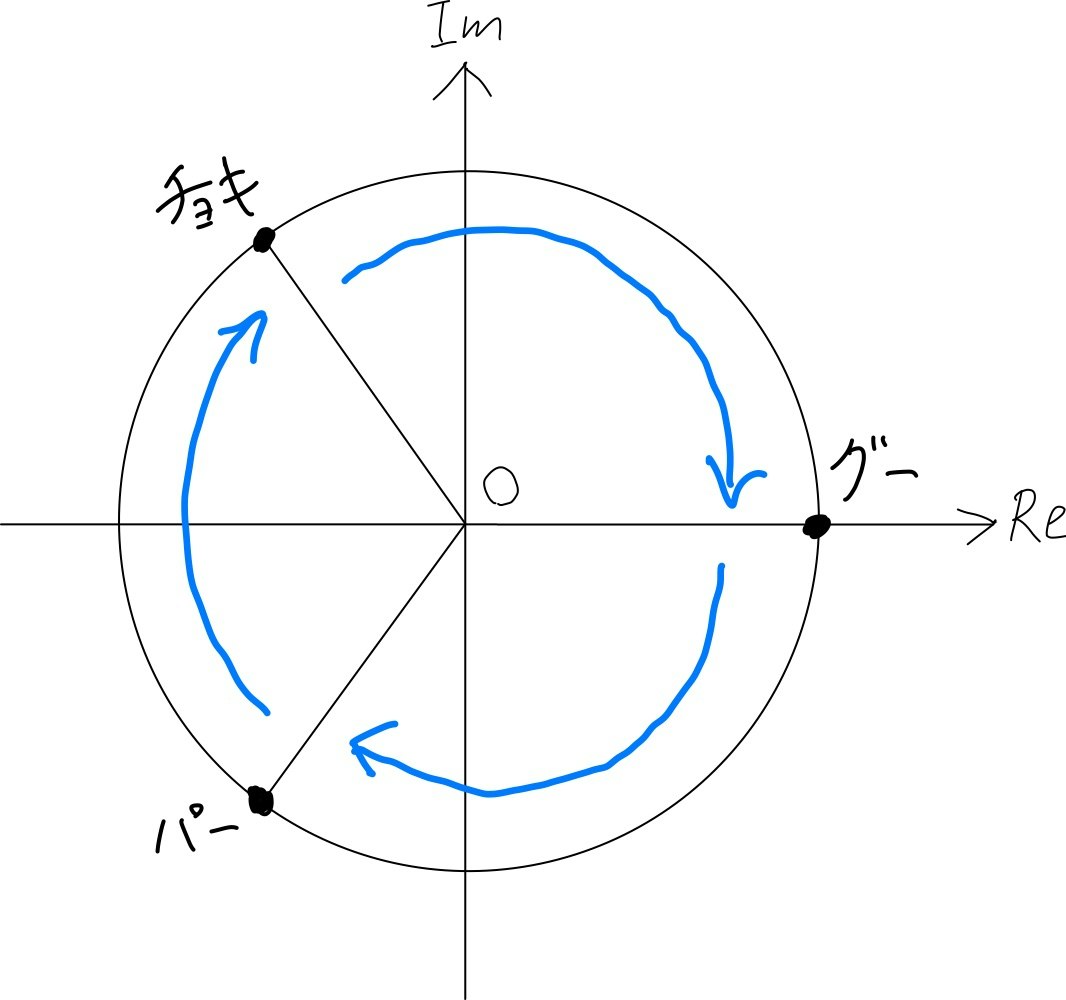 |
これを反時計回りすると「✊は✌に勝ち、✌は✋に勝ち、✋は✊に勝つ」という勝ちパターンが現れ、逆に時計回りすると「✊は✋に負け、✋は✌に負け、✌は✊に負ける」という負けパターンが現れる。
ここで、✊を反時計回りに120°ずらすと✌になるので、✊から✌への偏角
$$ \arg \frac{\text{SCISSORS}}{\text{ROCK}}$$
は+120°である。逆に、✌から✊への偏角
$$ \arg \frac{\text{ROCK}}{\text{SCISSORS}}$$
は-120°である。
(一般的に、反時計回りはプラスの角度で、時計回りはマイナスの角度として扱われる。また、偏角の主値は $(-180°,~+180°]$ とする。)
つまり、以下の手順で分母にした変数の勝敗を知ることができる。
- 対決させたい変数同士で割り算する。
- 偏角をとる。
- プラスかマイナスかゼロかを判別する。