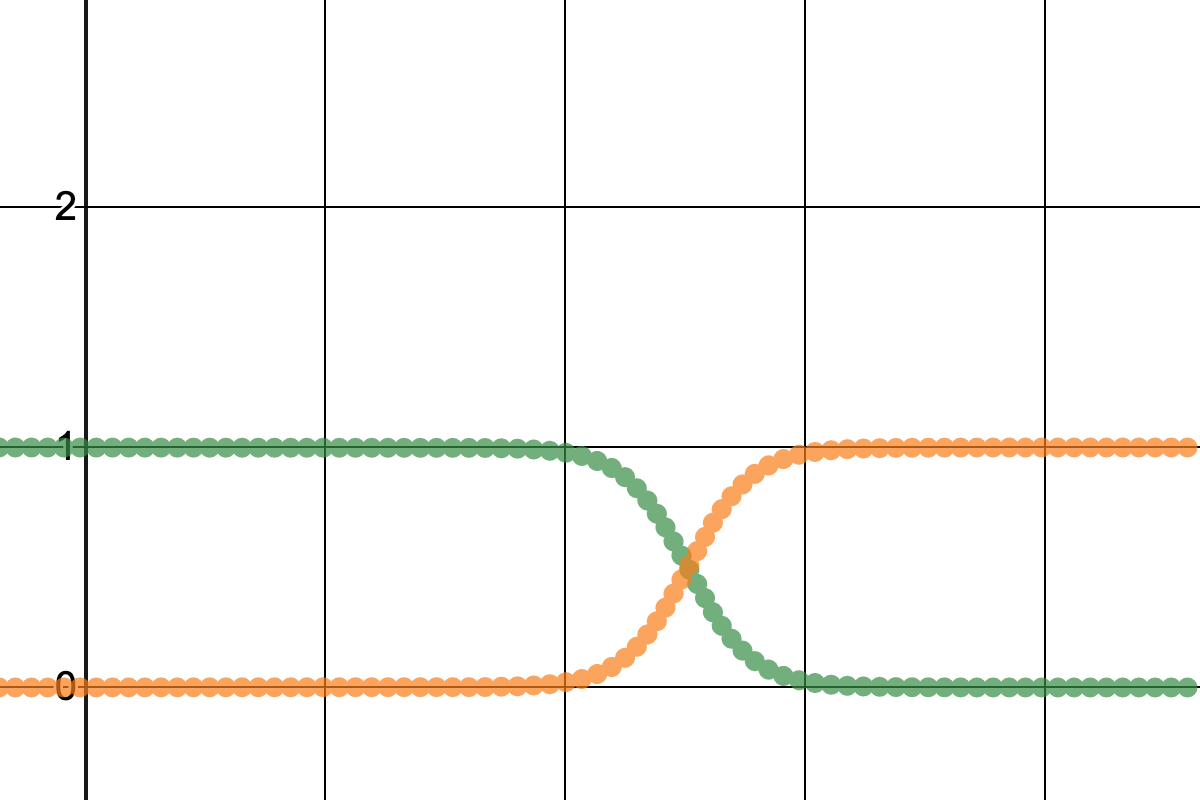
※この記事は、ベイズの定理に出てくるそれぞれの確率分布を幾何的にイメージしたときの筆者の脳内であって、数学的に厳密ではありません。
しかし個人的意見ですが、この記事のように数式にフリガナを振るようなことも理解を深めることに役立つと思います。
ベイズの定理
p(C_k|x) = \frac{p(x|C_k)p(C_k)}{p(x)}
ベイズの定理を使って事後確率 $p(C_k|x)$を求める過程を、尤度（クラス別密度） $p(x|C_k)$、生起確率（入力データの分布） $p(x)$のグラフを使ってイメージしたい。この記事では $k=1, 2$ で2クラス判別をする場合を考える。また、事前確率は $p(C_1) = p(C_2) = \frac{1}{2}$ とする。
尤度（クラス別密度）
尤度 $p(x|C_k)$ は以下のような分布をしていると設定する。
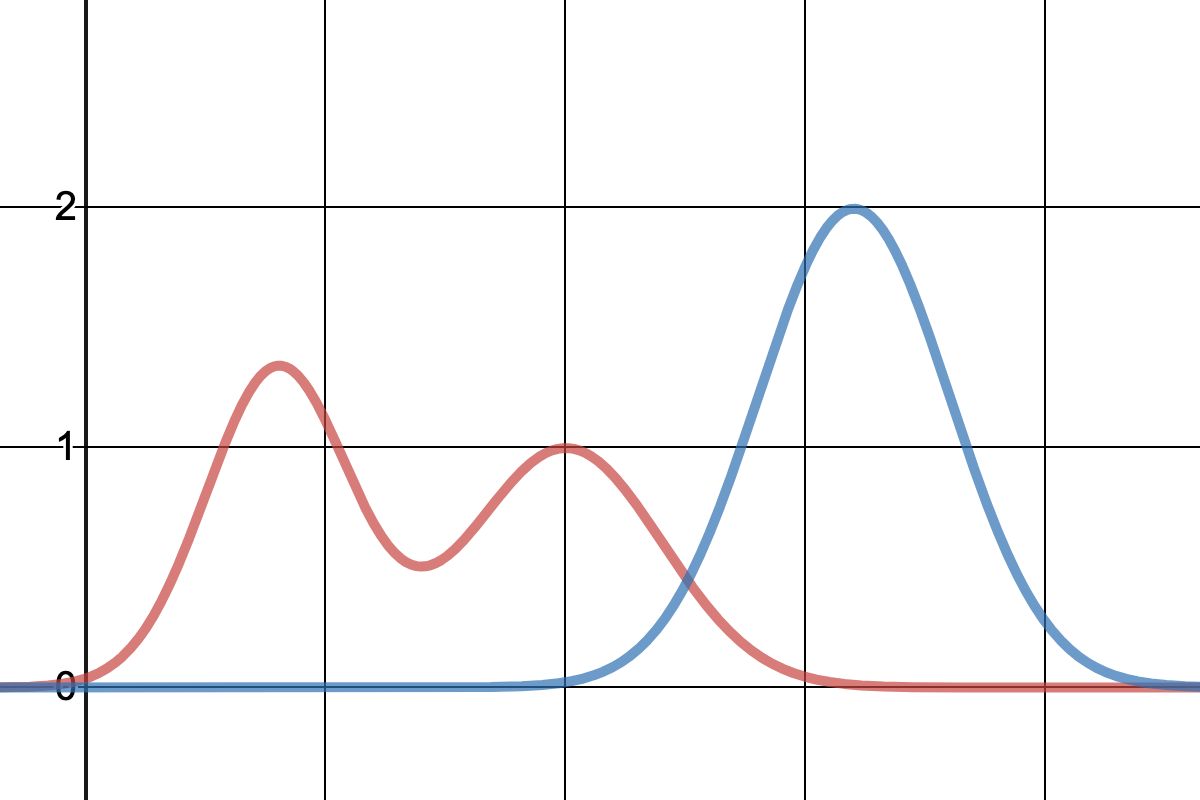
尤度は正規分布のような単純な分布ではなく複雑な分布を取り得るため、正確に尤度の分布を知るには大量のデータが必要になる。
生起確率(入力データの分布)
生起確率 $p(x)$ は
$$ p(x) = \sum_k p(x|C_k)p(C_k) = \sum_k p(x, C_k) $$
のように周辺化することで求められるから、下のグラフのようになる。
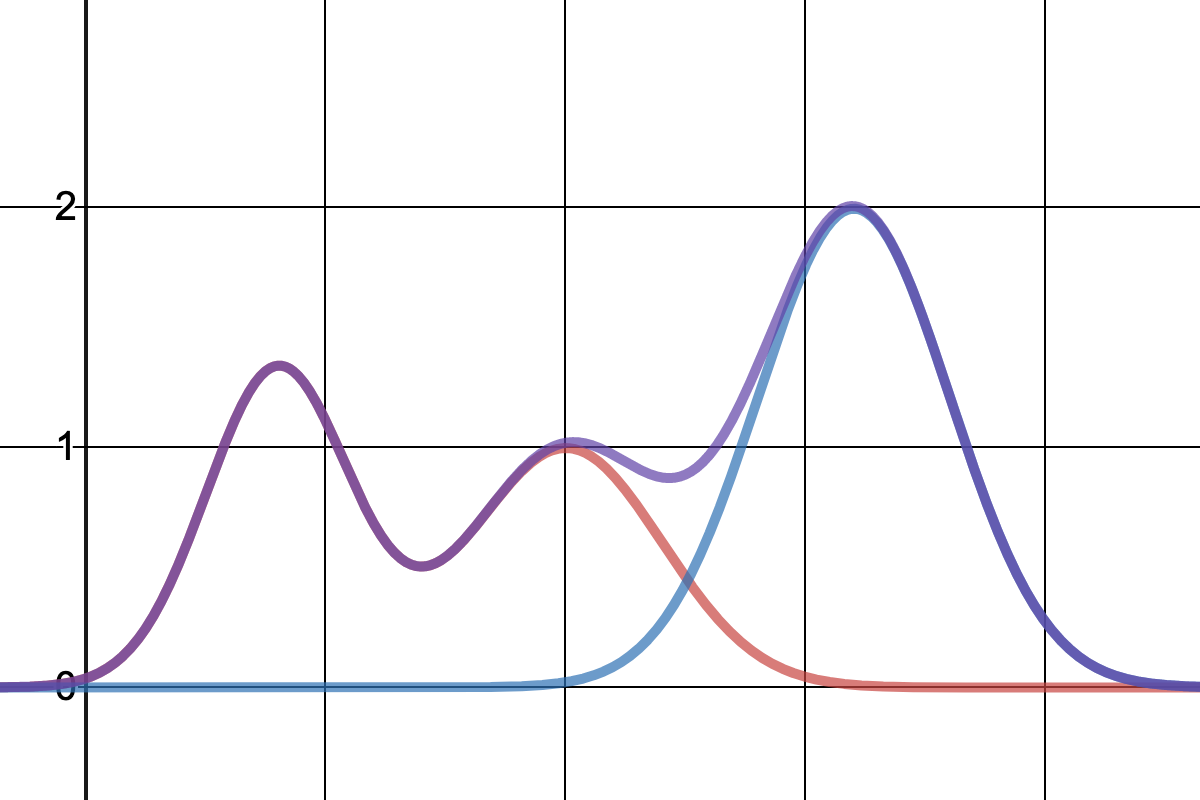
識別モデルと生成モデル（余談）
生起確率 $p(x)$ は $k$ に依存しない、つまり全クラス共通の係数であるから、クラス間の事後確率の大小のみを比較したい場合はわざわざ計算する必要がない。クラスの識別（分類）のみを目的とするなら余分な計算量となる。
しかし、$p(x)$ の意味を考えてみると、これは入力データの分布、つまりデータがどのように生じたかを表す分布と解釈できる。最近人気の架空のデータを生じさせる生成モデルは、この入力データの分布をもとにデータを出力している。
事後確率
$$ 事後確率 = \frac{尤度}{生起確率} \times 事前確率 $$
事後確率は上式で求められる。ちなみに、尤度と生起確率を、この記事中のグラフの色で置き換えると下のようになる。
$$ 緑 = \frac{赤}{紫} \times 事前確率 , 橙 = \frac{青}{紫} \times 事前確率 $$
実際に緑と橙を計算したものをプロットすると下のようになる。
先ほどの生起確率（紫）のグラフとこの事後確率（橙、緑）のグラフを一緒に眺めると、赤と紫がほぼ重なっている部分は緑がほぼ $1$ で一定になっていて、赤と紫がだんだん離れ始めると緑も下がり始める。
また、2つのグラフを同じ平面上にプロットすると下のようになる。
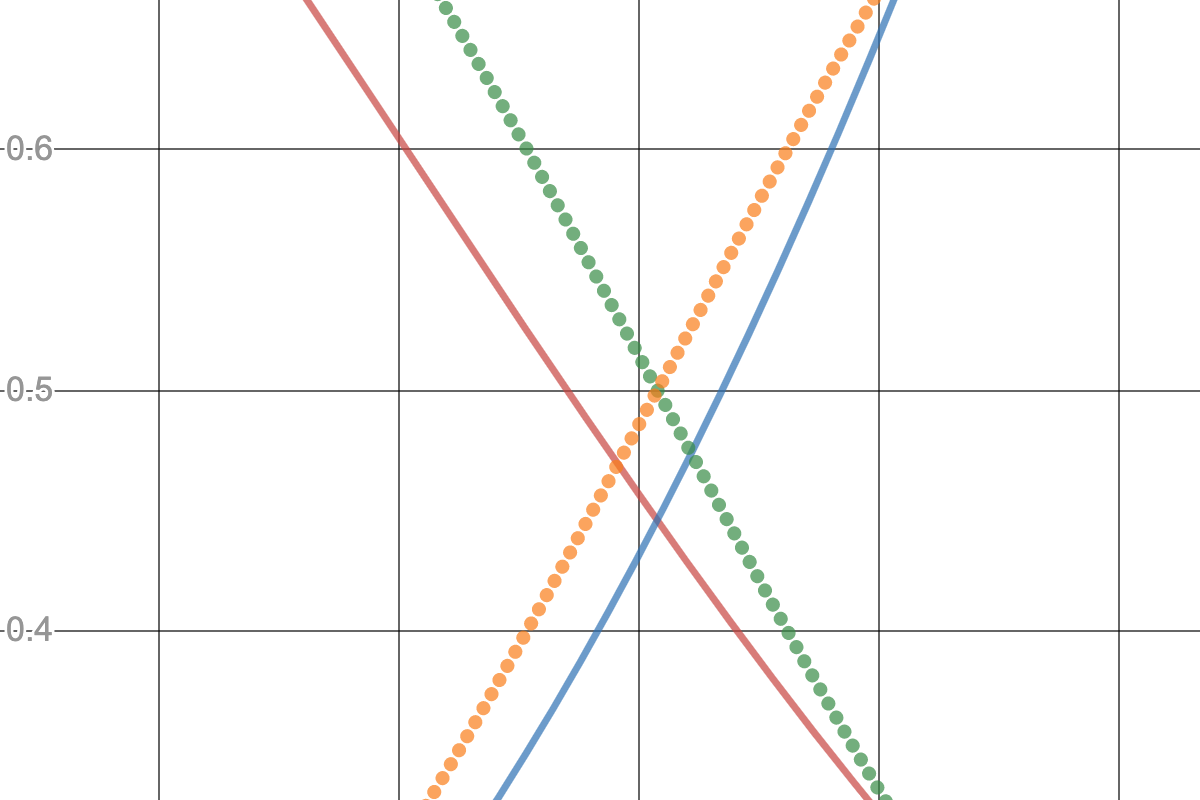
尤度（赤、青）が拮抗してる点で事後確率（橙、緑）は $\frac{1}{2}$ になる。つまり、尤度が一致したり近い値をとると、モデルはほぼランダムに識別する。
このような識別のもとになる確率を知ることができれば、確率が低い時に機械による判断を避けて人間に判断を委ねたりすることができる。（リジェクト）