最近,新型肺炎が流行っていますね.
以前にSIRモデルという感染症の数理モデルを使った研究をしていたので,新型肺炎のモデルに当てはめてみました.数理モデルを使うと,感染症の未来を予測できます.
今回は,発生の中心である 武漢湖北省(武漢を含む省) に注目して,感染症のモデル化と感染症の未来を予測します.
keyword
疫学, SIR model, nCoV-2019, 新型肺炎, 新型コロナウィルス
SIRモデル
SIRモデルは,感染した人数の推移を微分方程式として表したモデルです(Wikipediaでもわかりやすく解析されています). SIRモデルでは,感染症に対して人は3つの状態を取ると考えられます.
- 感染する可能性がある人 : S
- 感染している人:I
- 感染から治って免疫を獲得した人,または死亡した人 : R
時刻tにおける感染する可能性のある人,感染している人と感染から治った人をそれぞれS(t), I(t)とR(t)表記すると,SIRモデルは,
$$
\dot{S}(t) = -\beta S(t)I(t),\
\dot{I}(t) = \beta S(t)I(t) - \gamma I(t)\
\dot{R}(t) = \gamma I(t)
$$
と記述されます.
ここで,βは感染率を表し,γは回復率(+死亡率)を表しています.
感染者の増え方は,感染率β,感染する可能性がある人S(t)と感染している人I(t)に比例します.
死亡した人も感染を引き起こさないので,感染から治った人と同一視することに注意してください.
ここで,
$$
S(t) + I(t) + R(t) = N
$$
は一定となり,その地域の人口と一致します.
今回は,武漢 湖北省の人口を使います.
武漢 湖北省における新型肝炎の感染データをつかって,感染率βと回復率γを学習し,武漢の未来を予測します.
使ったデータ
感染データはkaggleに公開されているこちらから引用しています.
また,武漢 湖北省の人口データは,こちらのに記述されている2017年の人口統計データを用いています.
SIRモデルを使ったパラメーターの学習
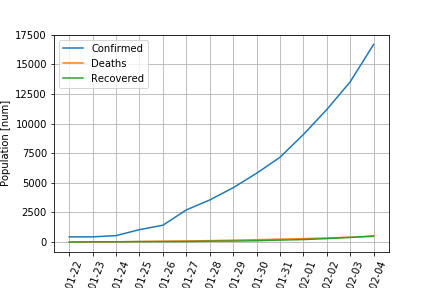
武漢 湖北省における,2020年1月22日から2月4日までの感染の推移は,以下のようになります.
青線が感染者数,オレンジ線が死者数,緑線が回復した人数です.
回復した人数と死者数がだいたい同じであることは,少しおかしいかな?と思います.
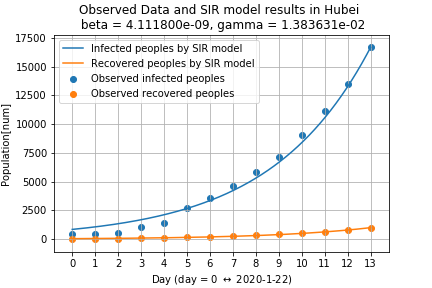
このデータを表現できるように,SIRモデルでフィッティングしてみました.
Recovered peopleは回復した人と死者数の和としています.
また,青点が実際に観測されている感染者数,青線がSIRモデルで近似した結果です.
オレンジ点とオレンジ線は回復した人数の実測値と予測値です.
十分に近似できていそうです.
武漢 湖北省の感染の未来を予測
十分に近似できていそうなので,学習したパラメータを使って, 武漢 湖北省の感染の未来を予測してみました.
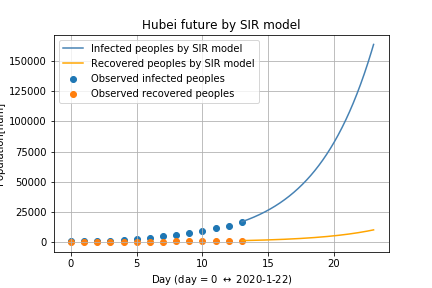
次の図が,2月4日から10日間の予測になります.
点が実測値,線が予測値です.
SIRモデルよれば,まだまだ増加するようです.
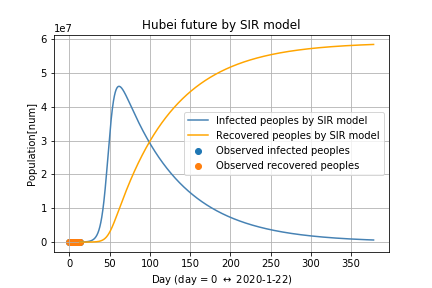
次が2月4日から一年間の予測になります.
感染が全然止まらいようです.
考察
- SIRモデルを用いて
武漢湖北省における新型肺炎の感染の拡大を予測してみましたが,拡大が止まらないという予測結果になりました. -
武漢湖北省において回復した人数が正確に計量されていないことが原因だと思われます. - 他のデータを用いて,回復率γを正確に測定できれば,より良い予測ができると考えられます.
今後の課題
次は,交通量をもとに,中国全土の感染の広がりを予測しようと思います.
追記: 基本再生産数 R0
病気の感染力は基本再生産数R0によって評価されます.
R0は無次元化した感染率β_hatと無次元化した回復率γ_hatの比で与えられます.よって,湖北省の基本再生産数R0は,
$$
R_0 = \frac{\hat{\beta}}{\hat{\gamma}} = \frac{\beta N^2}{\gamma N} \approx 17.54
$$
となります.
この値は麻疹(はしか)などの空気感染する病気と同じぐらいです.この感染力の強さは,考察で述べたように回復率が低く見積もられているからだと考えられます.
コード