LoginSignup
2
3

More than 3 years have passed since last update.

@yuji0001(Yuji Okamoto 岡本有司)

確率の先鋭化と平滑化のまとめ + 簡単な文書生成に応用

Posted at

最近．分子デザインの論文[1]を読んでいるのですが，確率の最スケーリング（rescaling）の話があったのでまとめてみました．

確率の再スケーリングは，離散確率分布の先鋭化（sharpening）や平滑化（smoothing）に使われます．

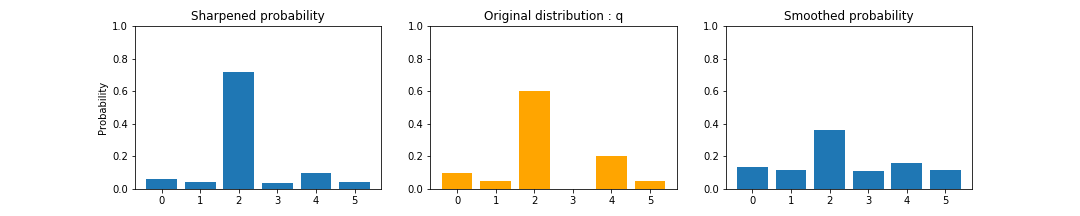
確率の先鋭化とは，高い確率をより高い確率に，低い確率をより低い確率に変換する操作です．
この操作によって，離散確率分布はOne-Hotな確率分布（ある要素のみ1それ以外は0）に近づきます．

一方で，確率の平滑化は，確率分布をなだらかにする操作です．
離散確率分布を一様分布に近づける操作となります．

sample.png

先鋭化と平滑化は，サンプル生成を確率分布を調整ときに用いられます．
自然言語処理の文書生成で先鋭化をもちいると，よりよく使われる文章が生成されます．
一方，平滑化を用いると，幅広い文章が生成されます．

この考え方は，自然言語処理のみではなく，教師なしクラスタリングや分子デザイン生成など，さまざまなところで用いられます．

ここでは，再スケールイング方法を2つほど紹介し，簡単な文章生成の問題で試してみます．

Thermal Rescaling

統計力学で使われるボルツマン分布を利用した手法です．
再スケーリング前の確率分布をq_i，再スケーリング後の確率分布をp_iとすると，Thermal Rescalingは以下のようになります．

$$
p_i = \frac{\exp(\frac{q_i}{T})}{\sum_{j}\exp(\frac{q_j}{T})}
$$

ここで，Tは温度パラメーターであり，Tが小さいと先鋭化され，Tが大きいと平滑化されます．
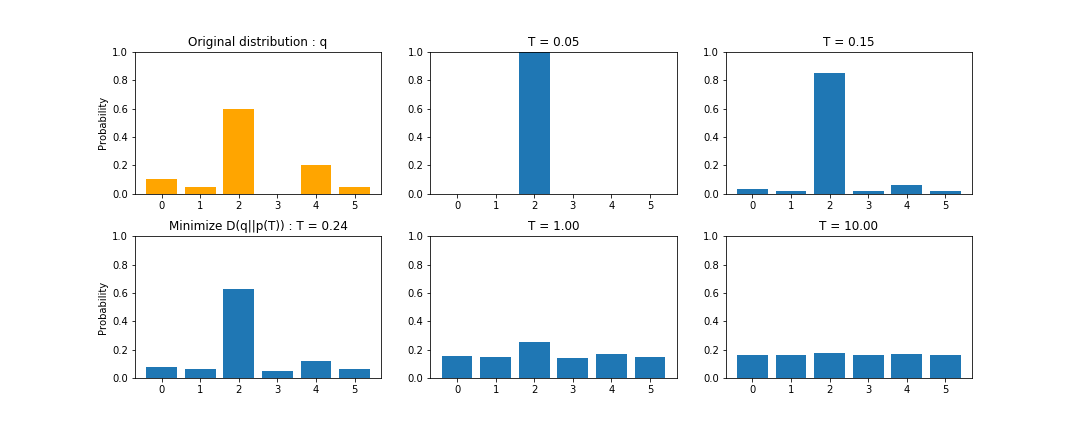
Thermal Rescalingによる確率分布の変化は以下のようになります．

example_thermal.png

Thermal Rescalingの特徴は以下の3点となります．
1. Tが0に近づくとOne-Hotな確率分布"v"に近づく.
2. Tが大きくなると一様分布"u"に近づく．
3. 変換前の確率分布と一致する温度パラメーター"T"があるとは限らない.

特徴3の系として，確率が0の要素が保存されないという特徴が重要です（上の図の要素3）.
この問題によって，再スケーリング前に想定していた確率分布のルールを壊す可能性があります．

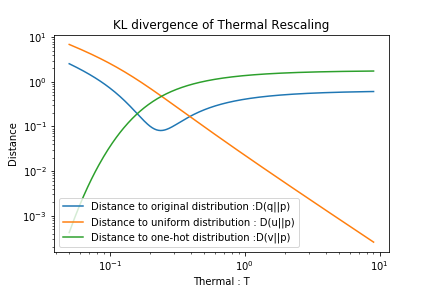
以下には再スケールング後の分布と（A）もとの分布q,（B）一様分布u,（C）One-hotな確率分布vとのそれぞれのKL情報量を示します．

KL_thermal.png

Tが0に近づくとOne-hotな確率分布vとのKL情報量は0に近づき，Tが大きくなると一様分布uとのKL情報量0に近づきます．
一方，もとの分布qとのKL情報量が0に近づくことはありません．

コードというほどではないですが，numpyを用いるなら以下のようになります．

# もとの離散確率分布
q = np.array([0.1,0.05,0.6,0,0.2,0.05])
# 温度パラメーター
T = 0.05
# 再スケーリング
p = np.exp(q/T) / np.sum(np.exp(q/T))

Freezing function

確率を指数倍する再スケーリング手法として，Freezing functionがあります．
教師なし学習手法，Deep Embedded Clustering (DEC)[2]にも，この考え方が用いられています．
再スケーリング前の確率分布をq_i，再スケーリング後の確率分布をp_iとすると，Freezing functionは以下のようになります．

$$
p_i = \frac{q_i^{\frac{1}{T}}}{\sum_{j}q_j^{\frac{1}{T}}}
$$

Thermal Rescalingと同様に，Tは温度パラメーターであり，Tが小さいと先鋭化され，Tが大きいと平滑化されます．
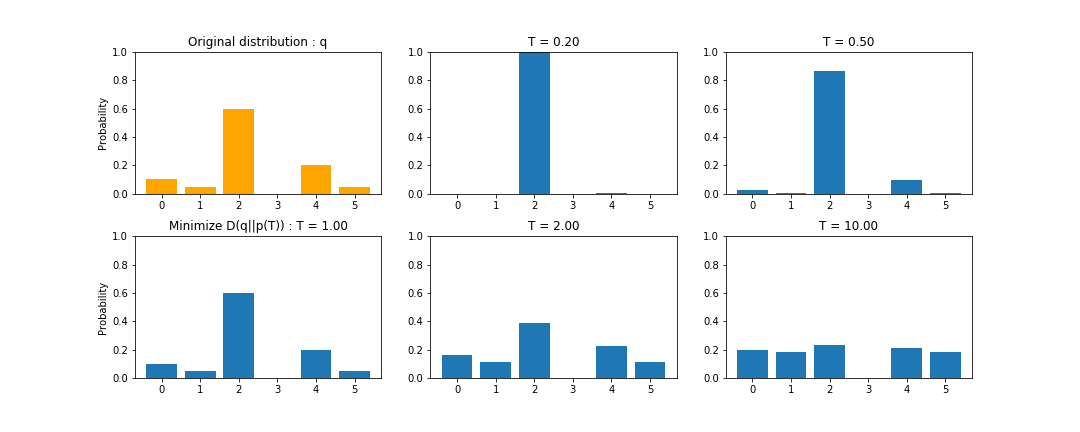
Thermal Rescalingによる確率分布の変化は以下のようになります．

example_freesing.png

Freezing functionの特徴は以下の3点となります．
1. Tが0に近づくとOne-Hotな確率分布"v"に近づく.
2. Tが大きくなってもと一様分布"u"に近づくとは限らない．
3. T=1の時, 変換前の確率分布と一致する.

Thermal rescalingとは異なり，確率0の要素が保存されます.
そのため，確率0の要素があると，平滑化によって一様分布にはなりません.

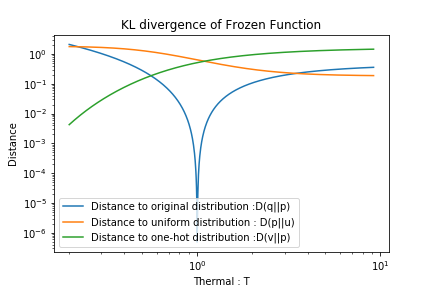
以下には再スケールング後の分布と（A）もとの分布,（B）一様分布u ,（C）One-hotな確率分布vとのそれぞれのKL情報量を示します．
（D(u||p)は計算できないのでD(p||u)を計算した．）

KL_freesing.png

Thermal rescalingと同様に，Tが0に近づくとOne-hotな確率分布vとのKL情報量は0に近づきますが，Tが大きくなっても一様分布uとのKL情報量0に近づきません．
一方で，T=1のとき，もとの分布qとのKL情報量は0に収束します．

コードというほどではないですが，numpyを用いるなら以下のようになります．

# もとの離散確率分布
q = np.array([0.1,0.05,0.6,0,0.2,0.05])
# 温度パラメーター
T = 0.2
# 再スケーリング
p = q**(1/T) / np.sum(q**(1/T))

文書生成への応用

以下の3つの文を学習に使います．

I have a pen. 
I have a dog. 
I buy a pen.

今回， 文章生成のモデルは簡単な，1-gramを用います．
1-gramを用いて10文ほど作成すると，以下のようになります．

 [SoS] I have a pen [EoS]
 [SoS] I have a pen [EoS]
 [SoS] I have a pen [EoS]
 [SoS] I have a pen [EoS]
 [SoS] I have a pen [EoS]
 [SoS] I have a dog [EoS]
 [SoS] I have a pen [EoS]
 [SoS] I buy a dog [EoS]
 [SoS] I buy a dog [EoS]
 [SoS] I have a pen [EoS]

一定の乱雑な，文章が生成されます．

まず，Freezing functionを用いて，先鋭化した文章は以下のようになります（T=0.1）．

 [SoS] I have a pen [EoS]
 [SoS] I have a pen [EoS]
 [SoS] I have a pen [EoS]
 [SoS] I have a pen [EoS]
 [SoS] I have a pen [EoS]
 [SoS] I have a pen [EoS]
 [SoS] I have a pen [EoS]
 [SoS] I have a pen [EoS]
 [SoS] I have a pen [EoS]
 [SoS] I have a pen [EoS]

"I" のあとに"have"をつかい，"a" のあとに"pen"をつかう学習用の文が多くいため，先鋭化により1つの文章のみが生成されるました．

次に，Freezing functionを用いて，平滑化した文章は以下のようになります（T=2.0）．

 [SoS] I have a dog [EoS]
 [SoS] I buy a dog [EoS]
 [SoS] I have a pen [EoS]
 [SoS] I have a pen [EoS]
 [SoS] I have a pen [EoS]
 [SoS] I have a dog [EoS]
 [SoS] I buy a dog [EoS]
 [SoS] I buy a pen [EoS]
 [SoS] I buy a pen [EoS]
 [SoS] I have a dog [EoS]

"I" のあとに"buy"をつかうサンプルが増加していますが，文章のルールが崩れることはありません．

最後に，Thermal rescalingを用いて，平滑化した文章は以下のようになります．(T=1.0)

 [SoS] a I have dog I have I [EoS]
 [SoS] [EoS]
 [SoS] have [SoS] I buy [EoS]
 [SoS] a a [EoS]
 [SoS] [SoS] [SoS] [EoS]
 [SoS] [EoS]
 [SoS] a buy a dog dog [SoS] I dog pen pen pen buy pen [EoS]
 [SoS] dog buy a I pen I have buy I buy a dog [EoS]
 [SoS] dog buy buy I dog a pen have dog pen [EoS]
 [SoS] I [SoS] buy dog [SoS] a pen pen [EoS]

文のルールが壊れます．
Thermal rescalingは確率0の要素を保存しないことが原因です．

以下に文章生成のコードを示します．．

import numpy as np

corpus = "I have a pen. I have a dog. I buy a pen."
# 文に分ける
sentences =  corpus.split('.')
# 空文の削除と[SoS],[EoS]の付加
sentences = ['[SoS] ' + s + ' [EoS]' for s in sentences if s != '']
# [EoS]→[EoS]の追加
sentences.append("[EoS] [EoS]")
# ダブルスペースの削除
sentences = [s.replace('  ',' ')  for s in sentences]
# ワードに分ける
words =[]
for s in sentences:
    words.append(s.split(' '))
# ワードリストの作成
word_list = ['[SoS]'] + list(set(sum(words,[])) - set(['[SoS]','[EoS]'])) + ['[EoS]']
# ワードリストを要素番号に変換
num_list = np.arange(len(word_list))
word_dict = dict(zip(word_list,num_list))
#遷移確率の作成
A = np.zeros((len(word_list),len(word_list)))
for s in words:
    for i in range(len(s) - 1):
        #数え上げ         
        A[word_dict[s[i+1]],word_dict[s[i]]] +=1
A = A / A.sum(axis = 0)
# Originalの文書生成
sentences_g = []

for i in range(10):
    #最初は[SoS]
    w = [0]
    while True:
        # 次の確率分布
        q = A[:,w[-1]]
        # sampling and append
        w.append(np.argmax(np.random.multinomial(1,q)))
        # if EoS then break
        if w[-1] == len(word_list)-1:
            break;
    # 文字列に変換            
    s = ''
    for i in w:
        s = s + ' ' +word_list[i]  

    #文書の追加 
    sentences_g.append(s)
# 表示
for s in sentences_g:
    print(s)

Freezing functonによるsharpeningのコード:

#  Sharpening by Freezing : T = 0.1
T = 0.1
sentences_g = []
for i in range(10):
    w = [0]
    while True:
        q = A[:,w[-1]]
        # 再スケーリング
        p = q**(1/T) / np.sum(q**(1/T))
        w.append(np.argmax(np.random.multinomial(1,p)))
        if w[-1] == len(word_list)-1:
            break;
    s = ''
    for i in w:
        s = s + ' ' +word_list[i]  
    sentences_g.append(s)
for s in sentences_g:
    print(s)

Thermal Rescalingによるsmoothingのコード:

#  Smoothing by Thermal : T = 1.0
T = 1.0
sentences_g = []
for i in range(10):
    w = [0]
    while True:
        q = A[:,w[-1]]
        # 再スケーリング
        p = np.exp(q/T) / np.sum(np.exp(q/T))
        w.append(np.argmax(np.random.multinomial(1,p)))
        if w[-1] == len(word_list)-1:
            break;
    s = ''
    for i in w:
        s = s + ' ' +word_list[i]  

    sentences_g.append(s)
for s in sentences_g:
    print(s)

偏りをつけて再スケーリングしたい場合

ある要素が現れやすい再スケールングをする場合があります．
その場合は，Gumbel-softmax関数[3]などを使うといいかもしれません．

再スケーリング前の確率分布を$q_i$，再スケーリング後の確率分布を$p_i$とすると，Gumbel-Softmax関数は以下のようになります．

$$
p_i = \frac{\exp(\frac{\log(q_i)+ g_i}{T})}{\sum_{j}\exp(\frac{\log(q_j)+ g_j}{T})}
$$

ここで，Tは温度パラメーターであり，今までの再スケーリングと同様に，Tが小さいと先鋭化され，Tが大きいと平滑化されます．
また，g_iは再スケーリング際に，優先度合いを決めるパラメーターです．
論文では，g_iを以下の分布から生成しています．

$$
g_i = -\log (-\log u),\quad u\sim {\rm Uniform}(0, 1)
$$

Gumbel-Softmax関数以外にも，偏りをつけて再スケーリングする手法はあると思います．
状況に応じて使っていきたいです．

まとめ

確率0の要素を保持したい場合はFreezing functionを使い，確率0の要素を保持したくない場合はThermal Rescalingを使うのがいいと思います．

code

Author

Yuji Okamoto: yuji.0001@gmail.com

Reference

[1] Elton, D. C., Boukouvalas, Z., Fuge, M. D., & Chung, P. W. (2019, August 1). Deep learning for molecular design - A review of the state of the art. Molecular Systems Design and Engineering, Vol. 4, pp. 828–849. https://doi.org/10.1039/c9me00039a

[2] Xie, J., Girshick, R., & Farhadi, A. (2015). Unsupervised Deep Embedding for Clustering Analysis. 48. Retrieved from http://arxiv.org/abs/1511.06335

[3] Jang, E., Gu, S., & Poole, B. (2019). Categorical reparameterization with gumbel-softmax. 5th International Conference on Learning Representations, ICLR 2017.

2
3
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
2
3