1. イベントトリガー制御とは
システムを制御する際に,リアルタイムに入力を更新できない場合が存在する.
イベントトリガー制御は,制御対象が安定となる逐次的な入力更新方法である.
医療の現場では「薬の投与」が入力の例になるが,リアルタイムに患者の状態を観測し,薬の投与を制御することができない.
そのため,どの程度の頻度で入力を制御する必要があるか知る必要がある.
ここでは,線形システムを用いたイベントトリガー制御を紹介する.
2.問題設定
可安定な線形時不変システム
$$
\dot{x}(t) = Ax(t) + Bu(t) \tag{1}
$$
を考える.可安定性から,ある比例制御入力( u(t) = Kx(t) )が存在し,フィードバック系
$$\dot{x}(t) = (A + BK)x(t)$$
の原点は漸近安定となる.
上記の比例制御入力では,リアルタイムなフィードバック制御を仮定しているが,実際の制御対象では必ずしもリアルタイムで入力を更新できない.
そのため,入力を逐次的に更新するイベント列を$ \{t_k \}_{k\in \mathbb{N}} $と定義し,逐次的な制御入力を
$$ u(t) = u(t_k) = Kx(t_k) ,\quad \forall t \in [t_k , t_{k+1}) $$
とする.
イベントトリガー制御では, システムが安定となる入力を更新するイベント列$ \{t_k \}_{k\in \mathbb{N}} $を設計する.
主結果[1]
線形時不変システム(1)に対して,逐次的なフィードバック制御を行うと,$t\in [t_k,t_{k+1})$における系のダイナミクスは
$$
\begin{align}
\dot{x}(t) &= Ax(t) + BKx(t_k) \
&= (A + BK)x(t) + BKe(t)
\end{align}
$$
となる.
ここで,$e(t)$はシステムの現在の状態と更新時の状態の差として
$$ e(t) := x(t_k) - x(t) $$
と定義されている.
正定行列$P$に対して,リアプノフ関数を
$$ V(x(t)) := x^{T} (t) P x(t) $$
と定義すると, 逐次的なフィードバック制御をされた系に沿った時間微分は
$$
\begin{align}
\dot{V} &= 2x^{T} (t) P(A+BK) x(t) + 2 x^{T} (t) PBK e(t) \
&=
[x^{T} (t)~e^{T} (t)]
\begin{bmatrix}
- Q & PBK\
K^{T} B^{T} P & 0
\end{bmatrix}
\begin{bmatrix}
x(t)\
e(t)
\end{bmatrix}
\end{align}
$$
となる.
ここで,
$$ Q: = - P(A+BK) - (A^{T} + K^{T} B^{T}) P $$
であり,システムの可安定性から$Q$は正定行列である.
リアプノフ関数を用いた安定性解析では, ある$ s \in (0,1) $ が存在し,
$$ \dot{V}(x(t)) \leq s x^{T}(t) Q x(t) $$
を満たすならば, 原点は漸近安定となる.
つまり,
$$
\Psi(x(t),e(t)) :=
[x^{T} (t)~e^{T} (t)]
\begin{bmatrix}
(s - 1) Q & PBK\
K^{T} B^{T} P & 0
\end{bmatrix}
\begin{bmatrix}
x(t)\
e(t)
\end{bmatrix}
\leq 0 \tag{2}
$$
を満たすならば, システムの安定化が達成される.
さて,フィードバック入力の更新時(つまり,$t = t_k$)ならば, $ e(t_k) = 0 $をみたすため,
$$
\begin{align}
\Psi(x(t_k),e(t_k)) &= (s -1) x^{T}(t_k) Q x(t_k)\
&<0,\quad x(t_k) \neq 0
\end{align}
$$
が成り立つ.
そこで,
$$ \Psi(x(t),e(t)) = 0 $$
を満たす時刻に, フィードバック入力を更新すれば,常に(2)をみたす.
まとめると,イベントトリガー制御は,フィードバックシステムが安定となる$K$を設計し,
$$ t_0 = 0,\quad t_{k+1} = \inf\{ t\in \mathbb{R} ~:~t>t_k \cap Psi(x(t),e(t)) = 0 \} $$
を更新タイミングとする制御機である.
例題
可制御な線形システム
$$
\dot{x}(t) =
\begin{bmatrix}
0 & 1 \
1 & -1
\end{bmatrix}
x(t) +
\begin{bmatrix}
1\
0
\end{bmatrix}
u(t)
$$
を考える.フィードバック入力を
$$ u(t) = K x(t) = [-2~0] x(t) $$
とすれば, システムは安定となる.
また,更新タイミングを決定するパラメータを
$$
s = 0.1,\quad
P =
\begin{bmatrix}
1 & 0 \
0 & 1
\end{bmatrix}
$$
とする.
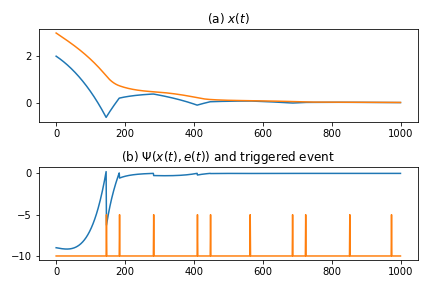
このときのイベントトリガー制御の結果を下の図に示す.
図(a)では,状態 $x$ の時間変化を表しており, 図(b)では, 更新の指針となる $\Psi(x,e)$ と更新が起きたタイミングを表している.
10回程度の更新を行うことにより,状態が原点に収束していることがわかる.
まとめと補足
イベントトリガー制御では, システムの安定に必要な制御入力の更新条件を与えた.
この更新条件は,状態$x$と更新誤差$e$を元に設計された関数$\Psi(x,e)$を元に設計された.
しかしながら, この更新条件を実システムに設計するには, 状態$x$と更新誤差$e$を常に観測する必要がある.
そこで,文献[1]では自己トリガー制御という手法が提案されている.
この制御手法の更新条件は,現在の状態$x$や更新誤差$e$は用いていないため,常に観測する必要がない.
次回は,この自己トリガー制御を紹介する.
参考文献
[1] Heemels, W. P. M. H., Johansson, K. H., & Tabuada, P. (2012). An introduction to event-triggered and self-triggered control (pp. 3270–3285). Presented at the 2012 IEEE 51st Annual Conference on Decision and Control (CDC).
サンプルコード
# いろいろインポート
import numpy as np
from matplotlib import pyplot as plt
%matplotlib inline
# モデルパラメータの設定
n = 2
A = np.array([[0,1],[1,-1]])
b = np.array([[1],[0]])
x0 = [2,3]
P = np.array([[1,0],[0,1]])
K = np.array([[-2,0]])
Q = - (A + b.dot(K)).dot(P) - P.dot(A + b.dot(K))
sigma = 0.1
# Event Trigger 関数の定義
def Psi(_x,_xk):
return (sigma - 1) * _x.T.dot( Q).dot(_x) + 2 * _x.dot(b).dot(K).dot(_xk - _x)
# 保存する変数の定義
N = 1000
h = 0.01
t = np.arange(N) * h
x = np.zeros([N,n])
event = np.zeros(N)
psi_list = np.zeros(N)
x[0] = x0
xk = x[0]
# 更新則
for k in range(N-1):
psi_list[k] = Psi(x[k],xk)
if Psi(x[k],xk)>= 0 :
xk = x[k]
event[k+1] = 1
x[k+1] = x[k] + h * (A.dot(x[k]) + b.dot(K).dot(xk))
# 結果の出力と保存
plt.subplot(2,1,1)
plt.plot(x)
plt.title('(a) $x(t)$')
plt.subplot(2,1,2)
plt.plot(psi_list)
plt.plot(-10 + 5 * event)
plt.title('(b) $\Psi(x(t),e(t))$ and triggered event')
plt.tight_layout()
plt.savefig('example.png')