はじめに
深層強化学習アルゴリズムの一つであるProximal Policy Optimization(通称PPO)をchainerを使って実装してみましたので、紹介します。
PPOの実装はchainerrlを始め、qiitaにも記事はたくさんあるので、何を今更感しかないのですが、qiitaに載っている記事は、Atariではなく、cart-poleのものが多そうだったので、今回はAtariでの結果と実装上の注意点を説明します。
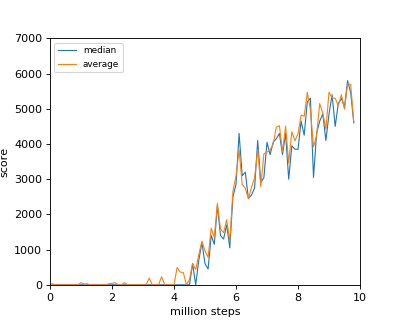
ちなみに他の手法だと学習がうまくいかないようなゲームも学習できたりします。例えば、こちらのZaxxonというゲームは学習が難しいですが、ppoなら学習が進みます。

Proximal Policy Optimizationって何?
Proximal Policy Optimizationは昔記事に書いたA3Cに似たアルゴリズムで、強化学習のアルゴリズムとしては大きくわけて3つある、Value-based、Policy-gradient、Actor-Critic(Policy-gradientとValue-basedを合わせたもの)アルゴリズムのうち、Actor-Criticに分類される手法です。
Proximal Policy Optimizationは、実装としてはA3Cに似ているところが多いですが、手法のルーツはTrust region policy optimization (TRPO)にあると考えることができ、Policy-gradientで逆伝搬をした際にパラメータ$\theta$が変わったことによって、新しい方策$\pi_{\theta_{\text{new}}}$と古い方策$\pi_{\theta_{\text{old}}}$が似ても似つかなることを防ぎ、Policy-gradientでの方策の改善を安定化させることを狙っています。
実際に実装はシンプルながら、A3Cなどと比較して良好な性能が出ることが知られています。
詳しい内容が知りたい方は、解説記事をこちらに書きましたので興味がある方は御覧ください。
実装上の注意点
基本的には以前書いた、DQNを卒業してA3Cで途中挫折しないための7Tips
で書いたTips1以外はほぼ同じです。それ以外に気をつけたほうが良さそうな点をここに書きます。
巷には2種類のネットワーク構造による実装が存在する
PPOの論文は、Atariの実装に関して、Mnihらの2013年版DQNのネットワーク構造を使ったと書いてあります。これは、2層のconvolutionレイヤーの後に、2層の全結合レイヤーがある構造です。ただ、いろいろみてみるとNature版DQNで使われたネットワーク構造を使った実装がたくさん見つかり、これは3層のconvolutionレイヤーの後に、2層の全結合という構造になっています。記事の最後に結果を載せますが、どうも2013年版DQNの構造より、Nature版DQNのネットワーク構造のほうが性能が良いらしく、それゆえ3層のconvolutionレイヤーを使った実装が多いようです。(OpenAIの本家実装も2パターン書いてある)
Generalized Advantage Estimator(GAE)の計算がややこしい
A3Cのときも次のAdvantage
A(s_{t}, a_{t}) = Q(s_{t}, a_{t}) - V(s_{t})
という量を計算します。実際には右辺を展開して($\lambda$は省略されています)、
\begin{align}
A(s_{t}, a_{t}) &= r_{t+1} + \gamma V(s_{t+1}) - V(s_{t}) \\
&= r_{t+1} + \gamma r_{t+2} + \gamma^{2} V(s_{t+2}) - V(s_{t}) \\
&= r_{t+1} + \gamma r_{t+2} + \gamma^{2} r_{t+3} + \cdots + \gamma^{T} V(s_{t+T}) - V(s_{t})
\end{align}
であると解釈して、得られる時系列$t$から$t+T$のデータから、逆向きにadvantageを次のように計算します
\begin{align}
A(s_{T}, a_{T}) &= r_{T+1} + \gamma V(s_{T+1}) - V(s_{T}) \\
A(s_{T-1}, a_{T-1}) &= r_{T} + \gamma(r_{T+1} + \gamma V(s_{T+1})) - V(s_{T-1}) \\ &= r_{T} + \gamma V(s_{T}) - \gamma V(s_{T}) + \gamma(r_{T+1} + \gamma V(s_{T+1})) - V(s_{T-1})\\
&= r_{T} + \gamma V(s_{T}) - V(s_{T-1}) + \gamma A(s_{T}, a_{T}) \\
&\dots \\
A(s_{t}, a_{t}) &= r_{t} + \gamma V(s_{t+1}) - V(s_{t}) + \gamma A(s_{t+1}, a_{t+1})
\end{align}
このとき、ある状態$s_{t'}$が最終状態の場合、アドバンテージ$A(s_{t'+1}, a_{t'+1})$は0であると解釈して、計算する必要があるところに注意が必要です。
結果
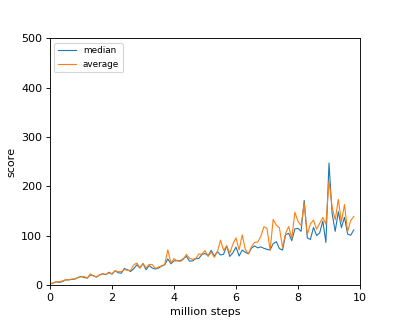
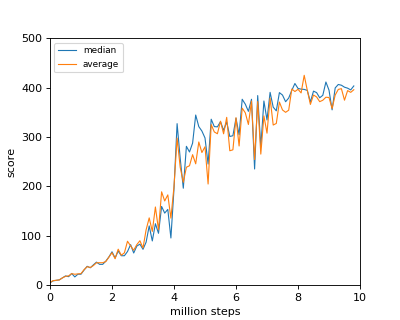
おなじみのBreakoutの結果を貼っておきます。(コードはこちら)やはり、Nature版DQNの構造のほうが性能が高いのが、わかります。
2013年版DQNのネットワーク構造による結果
| result | score |
|---|---|
 |
 |
Nature版DQNのネットワーク構造による結果
| result | score |
|---|---|
 |
 |
おまけ(Zaxxon)
| result | score |
|---|---|
 |
 |