誤りがありましたらご指摘よろしくお願いいたします!!
この記事を書くにあたり参考にさせていただいた文献は最後に参考文献としてまとめさせていただきました.
1. 始めに
今回は感染症の数理モデルであるSIRモデルについて扱う.
SIRモデルは世界初の感染症数理モデルであり,1927年に提案された[1].
以下では,SIRモデルの理論の解説,シンプルなPythonでのシミュレーションの実装を行う.(より面白いシミュレーションは参考文献[3]が超分かりやすかったでおすすめさせていただきます.)
2. SIRモデルの理論
2.1 モデルの規則
SIRモデルの規則は次の通りである.
(1) 初期状態として,人口全体を健康Susceptible(S), 感染者Infected(I), 免疫獲得者Recovered(R)の3グループに分ける.
(2) SはIから感染し得る.Sが微小時間$\Delta t$の間に感染しIになる確率は,$\lambda \times \rm{隣接するIの人数} \times \Delta t$である.ただし$\lambda$は感染率である.
(3) Iの人は時間$\Delta t$の間に確率$\mu\Delta t$でRになる.ただし$\mu$は治癒率.
補足
・Rは免疫獲得者であり,Sを感染させることは無く,再度Iになることもない.
・最終的にはSとRだけになる.最後に残ったRの数が感染の大きさを表す.
2.2 モデルの定式化
時刻$t$におけるS, I, Rの数をそれぞれ$S(t)$, $I(t)$, $R(t)$,$\lambda$は感染率,$\mu$は治癒率とする.
まずこれから,$S(t)$, $I(t)$, $R(t)$が満たす関係式を導出する.
健康な人Sが感染するとIになるので,Sが減少した分Iは増える.また,健康な人が多いほど感染者は増加しやすくなる.このことから,
$$
\begin{equation}
\frac{dS(t)}{dt} = -\lambda I(t)S(t)
\end{equation}
$$
が得られる.
免疫獲得者Rについても同様に考えて,
$$
\begin{equation}
\frac{dR(t)}{dt} = \mu I(t)
\end{equation}
$$
ここで,人口全体の数を$N$とすると,
$$
\begin{equation}
S(t) + I(t) + R(t) = N
\end{equation}
$$
が成り立つので,この式の両辺を$t$で微分して,
$$
\begin{equation}
\frac{dS(t)}{dt} + \frac{dI(t)}{dt} + \frac{dR(t)}{dt} = 0
\end{equation}
$$
この式に,(1), (2)式を代入し整理して
$$
\begin{equation}
\frac{dI(t)}{dt} = \lambda I(t) S(t) - \mu I(t)
\end{equation}
$$
を得る.
以上で求めた,$S(t)$, $I(t)$, $R(t)$それぞれに関する式を改めて書く.
\begin{align}
\frac{dS(t)}{dt} &= -\lambda I(t)S(t) \tag{1}\\
\frac{dI(t)}{dt} &= \lambda I(t) S(t) - \mu I(t) \tag{2}\\
\frac{dR(t)}{dt} &= \mu I(t) \tag{3}
\end{align}
これら3つの常微分方程式でSIRモデルを表すことが出来る.
3. SIRモデルのシミュレーション
3.1 方法
(1)~(3)式からS(t),I(t),R(t)の時間発展をグラフにしたい.この連立常微分方程式を解析的に解くことは困難であるので冪級数展開の1次までの近似を用いる.
ここで軽く,冪級数展開について振り返る.
関数$f(t)$の$t = a$周りの展開は,
$$
\begin{equation}
f(t) = \sum ^\infty_{n=0} \frac{f^{(n)}(t)}{n!} (t - a)^n
\end{equation}
$$
であり$n=1$の項まで求めて,$\Delta t = t - a$とおけば,
$$
\begin{equation}
f(a + \Delta t) \simeq f(a) + f'(a) \Delta t \tag{4}
\end{equation}
$$
が得られる.この式は,ある時刻$t = a$から$\Delta t$だけ経った時刻での関数$f$の値を返すと言える.
今回のモデルでは(4)式の$f'$に相当するものは求まっているので,初期状態を決めれば,簡単にシミュレーション出来る.
3.2 Pythonでの実装と結果
シンプルに実装すると以下の様になる.
import matplotlib.pyplot as plt
import tqdm
# 初期条件
S = 0.99
I = 0.01
R = 0.
t = 0
# 各パラメータの設定
infetion_rate = 1.7
healing_rate = 0.8
loop_num = 3000
delta_t = 0.01
# 結果記録用のリスト
t_list = []
S_list = []
I_list = []
R_list = []
for _ in tqdm.tqdm(range(loop_num)):
t += delta_t
new_S = S + delta_t * (-infetion_rate * S * I)
new_I = I + delta_t * (infetion_rate * S * I - healing_rate * I)
new_R = R + delta_t * (healing_rate * I)
t_list.append(t)
S_list.append(new_S)
I_list.append(new_I)
R_list.append(new_R)
S = new_S
I = new_I
R = new_R
fig = plt.figure()
plt.plot(t_list, S_list, label='S')
plt.plot(t_list, I_list, label='I')
plt.plot(t_list, R_list, label='R')
plt.title('Population Rate-Time')
plt.xlabel('Time')
plt.ylabel('Population Rate')
plt.legend()
plt.show()
fig.savefig('./SIR_P-T.png')
print('\n --DONE-- \n')
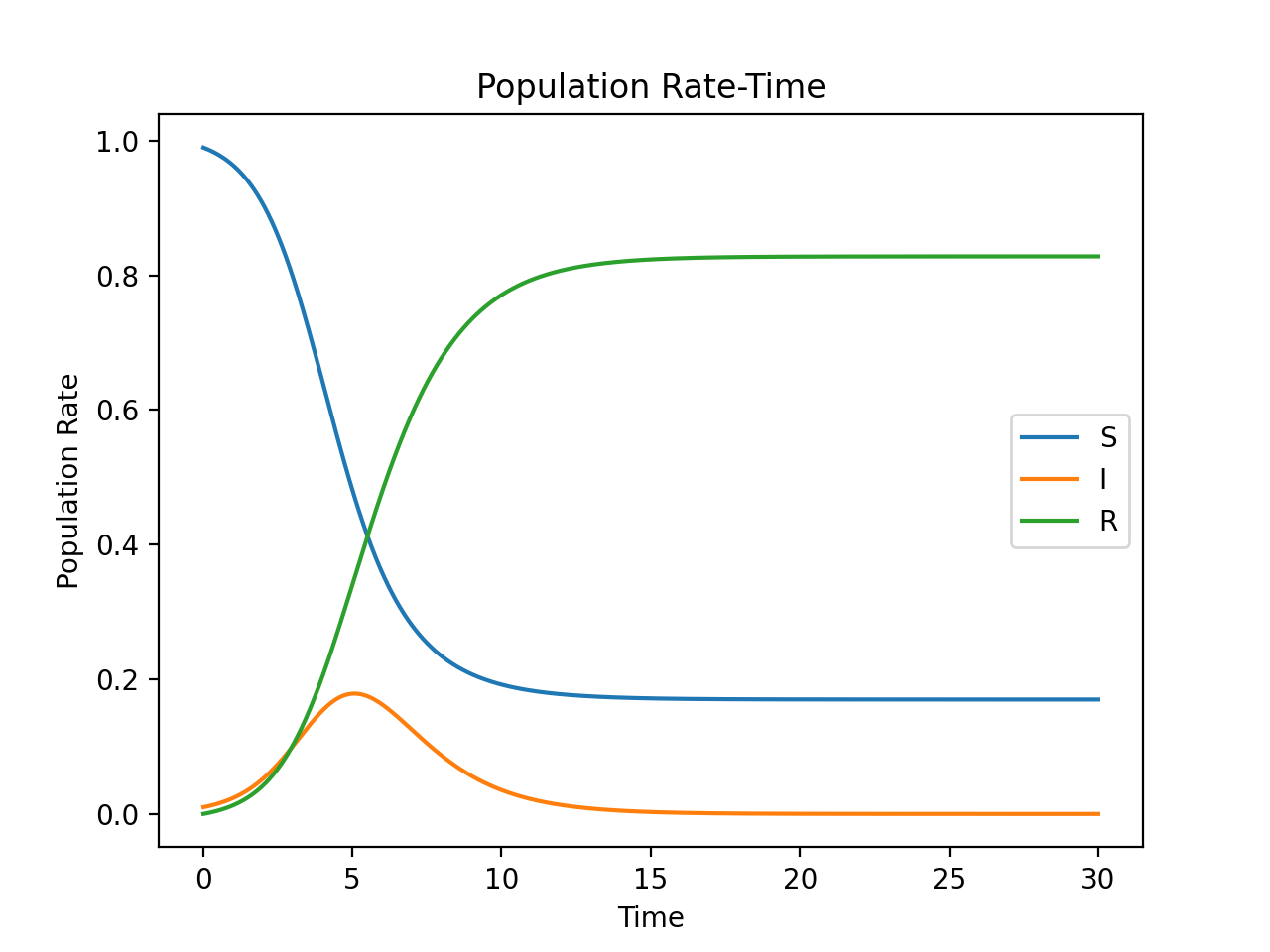
結果のグラフを以下に示す.
$t=5$くらいの時に感染者数のピークが来ていて,その少し後に,健康な人と免疫獲得者の割合が同じになっている.
4. SIRモデルの発展型
4.1 SEIRモデル
病原体が十分増殖する潜伏期間Exposed(E)を加えたモデルである.つまり,状態の遷移の流れはS→E→I→Rとなる.このモデルを式に表すと,
\begin{align}
\frac{dS(t)}{dt} &= -\lambda I(t)S(t) \\
\frac{dE(t)}{dt} &= \lambda I(t)S(t) - \epsilon E(t) \\
\frac{dI(t)}{dt} &= \epsilon E(t) - \mu I(t)\\
\frac{dR(t)}{dt} &= \mu I(t)
\end{align}
と書ける.ただし$\epsilon$は潜伏期間の逆数である.
このモデルはより,実際の感染症に近いですね.
4.2 SEIRDモデル
このモデルは感染症で亡くなることを考慮して,状態Died(D)を追加したモデルである.状態の遷移はS→E→I→R or D となる.
死亡率を$\alpha$,亡くなるまでにかかる平均の日数の逆数を$\rho$とすると,このモデルを表す式は,
\begin{align}
\frac{dS(t)}{dt} &= -\lambda I(t)S(t) \\
\frac{dE(t)}{dt} &= \lambda I(t)S(t) - \epsilon E(t) \\
\frac{dI(t)}{dt} &= \epsilon E(t) - (1-\alpha) \mu I(t) -\alpha \rho I(t)\\
\frac{dR(t)}{dt} &= (1-\alpha)\mu I(t) \\
\frac{dD(t)}{dt} &= \alpha \rho I(t)
\end{align}
5. まとめ
今回メインで扱ったSIRモデルは世界初の感染症の数理モデルで,とてもシンプルに,人口を健康な人,病人,免疫獲得者の3つに分けてモデル化しました.山火事の広がり方のモデルにも応用出来るそうです.(この場合,木,燃えてる木,燃え終わった木の3つに分ける.)
参考文献[3]では,人を止めたり,動かしたりしてそれが感染拡大にどの様に影響するのかを分かりやすく視覚化されていました.ぜひ見てみてください!
雑感
前々から興味があったので簡単にではありますが,まとめてみました!SIRモデルの式を導出したときと同じ様な手順で様々は状態を追加して,用意に拡張できるところが良いなと思いました.
勉強するだけなら難しい数学とか実装とか無しに出来て面白いシミュレーションがたくさんあるので今後も見ていきたいです.
この記事では扱っていませんが,参考文献[2]ではSIRモデルやSISモデル,その他の数理モデルについて理論的に書かれています.興味のある方にはおすすめです!
今後は,数理経済学の国際経済モデルの論文を読んでとてもおもしろかったので書けたら良いなと思います.アクティブマター系のモデルのVicsek modelとかも面白かったしそれもまた今度.そんなことより卒研がやばい.がんばります.
最後までありがとうございました.
参考文献
[1] A contribution to the mathematical theory of epidemics
[2] 増田直紀,今野紀雄著,複雑ネットワーク 基礎から応用まで
[3] https://github.com/tamaki-py/simulasir/blob/master/simulasir.py
[4] 感染症の数理モデルと対策
[5] 感染症のSIRモデル発展編 【数理モデルの拡張】