作図パッケージ Compose.jl の使い方

この記事について

Julia Advent Calendar 2016 24日目の記事です。

私は生物系データの解析手法開発やデータ解析をおこなうバイオインフォマティクスの研究者です。普段はJuliaをスクリプトを書くのに使うライトユーザーです。

今回はCompose.jlという作図パッケージについて紹介したいと思います。簡単にプロットを作るためのパッケージではなく、作図関数を作るためのライブラリというイメージが近いと思います。

Julia の作図用パッケージ

Julia には作図のためのパッケージがいくつかあります。有名なものを挙げます。

• Gadfly
  • http://gadflyjl.org/stable/
• Compose
  • http://giovineitalia.github.io/Compose.jl/latest/#Compose-1
  • IJulia で表示される
    • http://julia-programming-language.2336112.n4.nabble.com/Compose-jl-drawing-in-IJulia-td40227.html
• Pyplot
  • https://gist.github.com/gizmaa/7214002
• Cario
  • https://github.com/JuliaGraphics/Cairo.jl
• Luxor
  • https://github.com/cormullion/Luxor.jl
• Winston
  • https://github.com/nolta/Winston.jl

Compose とは？

Compose は Gadfly のバックエンドとして開発されました。

ComposeはRでいうところのGridパッケージに相当するものとして設計されており、実際RのGridパッケージによく似ています。

Gadfly uses a custom graphics library called Compose, which is an attempt at a more elegant, purely functional take on the R grid package.
http://gadflyjl.org/stable/tutorial.html

Compose で図を作るのははっきり言って少し面倒ですが、思った通りの図を作れるのがオススメです。

Composeを選ぶ理由

単にデータをプロットするならばPyPlotやGadflyといった優れたユーザフレンドリなパッケージが存在します。

Composeは円や線といった基本的なオブジェクトを

実際、Composeを使おうと思ったのは、作図関数を自分作りたい用途があったためです。

使い始める前に

ドキュメントが未完成

現状ではドキュメントはチュートリアルのみが書かれています。

これは開発者のGiovineItaliaさんが同じく開発しているGadflyの方に集中されているからなのかなと推察しています（余裕があれば自分もドキュメントづくりをお手伝いしたいところです）。

Jupyter notebookでやるといいよ

JuliaのREPLでは（少なくとも現在の私の環境では）インタラクティブに図を表示できません。Composeの戻り値はそのままtypeが表示されます。

一方で、Jupyter notebookでComposeを使うとインタラクティブに図を表示できます。

以下のコマンドでJupyter notebook上での図のサイズを変更できます。

Compose.set_default_graphic_size(5inch, 5inch)

参考: http://julia-programming-language.2336112.n4.nabble.com/Compose-jl-drawing-in-IJulia-td40227.html

Compose の基本

Composeでは図を木構造として表現します。

そこで重要なのが３種類のノード（Context, Form, Property）とcompose()関数です。

３種類のノード: Context, Form, Property

Composeにおける木は、以下の３種類のノードから成ります。

• Context: 内部ノードになる

• Form: 形を定義する葉（例: line, polygon）

• Property: 葉ノードであり、かつ、親ノードの部分木の見た目を指定する（例：色、フォント、線の太さ）

compose()による木構造の指定（基本）

３種類のノードの関係を定義するのがcompose()関数です。
compose(a, b) という書き方で、 a が根でbがその子ノードとなる木を作ります。

わかりづらいと思うので具体例で説明します。

まず、一つのContextの子ノードとしてFormの一種である rectangle を指定します。context()はContextオブジェクトを生成し、rectangle()はFormオブジェクトを生成します。

# typeof(context())
Compose.Context

# typeof(rectangle())
Compose.Form{Compose.RectanglePrimitive{Tuple{Measures.Length{:w,Float64},Measures.Length{:h,Float64}},Measures.Length{:w,Float64},Measures.Length{:h,Float64}}}

compose(a, b)とすることで context()に長方形を表示させることができます（デフォルトだと、長方形の大きさはContextと同じで、かつ色が黒のため、単に黒い画面になります）。

c1 = compose(context(), rectangle())

また、compose()の戻り値も Context です。

# typeof(c1)
Compose.Context

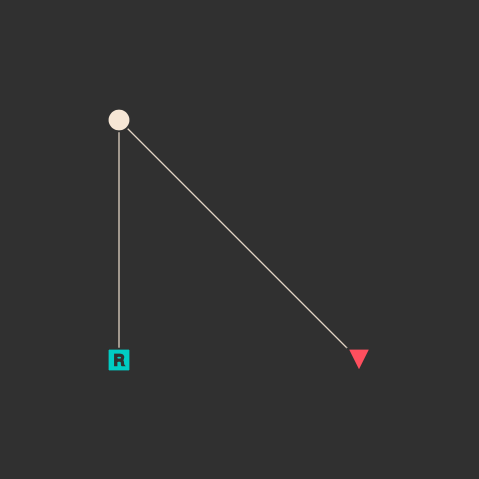
introspect()関数を使うことで木構造を可視化することができます。丸がContextで四角がFormです。

introspect(c1)

次に、Propertyも追加してみましょう。fill()はPropopertyオブジェクトを返します。

c2 = compose(c1, fill("tomato"))

fill()はPropopertyオブジェクトを返します。

# typeof(fill("tomato"))
Compose.Property{Compose.FillPrimitive}

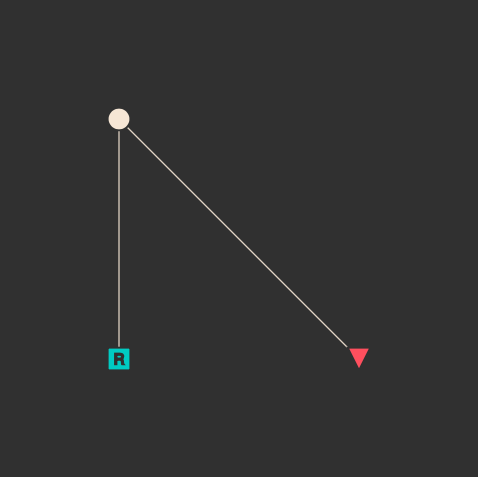
木構造をみると、第二引数が第一引数の根の子ノードになることがわかります。

introspect(c2)

また、compose!()という関数も用意されています。これは（!がついていることからわかるように）第一引数を上書きします。

compose()による木構造の指定（S式）

先ほどの例では合計２回compose()を実行しましたが、これは１回で済む書き方もあります。
compose() は
（Lispユーザーや系統進化学をやっている方には馴染み深い記法かと思います）。

先ほどと同じ図を compose(a, b, c) という書き方でもできます。

c3 = compose(context(), rectangle(), fill("tomato"))

introspect(c3)

部分木を組み合わせる

compose()関数では、部分木を括弧でくくることにより、多くの部分木をいっぺんに組み合わせることができます。

c4 = compose(context(),
        (context(), circle(), fill("bisque")),
        (context(), rectangle(), fill("tomato")))

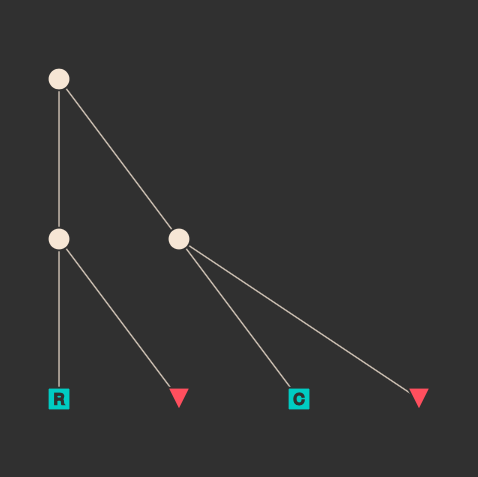
introspect(c4)

Contextによる子ノードの座標系の指定

Contextでは子ノード（およびその下のノード）の座標系を指定できます。
context(x0, y0, width, height)という形でx座標の始まり、y座標の始まり、x座標の幅、y座標の幅を指定できます。デフォルトは(0, 0, 1, 1)であり、x、y座標ともに[0,1]である平面を指定していることになります。

例をみてみましょう。１つ目の円はcontext(0.0, 0.0, 0.5, 0.5)で指定される部分平面に(0, 0, 1, 1)という座標系ができています。２つ目の円はcontext(0.5, 0.5, 0.5, 0.5)で指定される部分平面に(0, 0, 1, 1)という座標系ができています。

compose(context(), fill("tomato"),
        (context(0.0, 0.0, 0.5, 0.5), circle()),
        (context(0.5, 0.5, 0.5, 0.5), circle()))

部分平面と座標系の違いがわかりやすいように、左上の円の大きさを変えてみます。円はcircle(中心のx座標, 中心のy座標, 半径)と指定します。

これをみると context(0.0, 0.0, 0.5, 0.5) で指定された部分平面に収まるように、もとのContextのデフォルトの座標系(0, 0, 1, 1)が設定されていることがわかると思います。

compose(context(), fill("tomato"),
        (context(0.0, 0.0, 0.5, 0.5), circle(0.5, 0.5, 0.25)),
        (context(0.5, 0.5, 0.5, 0.5), circle()))

さらにcontext()にunitsという引数を与えることで、座標系も変更することができます。
下の例では、左下の円のcontext()で座標系を変更し、さらにcircle()で指定するxy座標と半径のスケールもこれまでと違うことがわかります。

compose(context(), fill("tomato"),
        (context(0.0, 0.0, 0.5, 0.5), circle(0.5, 0.5, 0.25)),
        (context(0.5, 0.5, 0.5, 0.5, units = UnitBox(0, 0, 100, 100)), circle(50, 50, 25)))

さらに図をどんどん入れ子にしていくこともできます。

c5 = compose(context(), fill("tomato"),
        (context(0.0, 0.0, 0.5, 0.5), circle(0.5, 0.5, 0.25)),
        (context(0.5, 0.5, 0.5, 0.5, units = UnitBox(0, 0, 100, 100)), circle(50, 50, 20)))

c6 = compose(context(),
        (context(units=UnitBox(0, 0, 1000, 1000)),
         polygon([(0, 1000), (500, 1000), (500, 0)]),
         fill("tomato")),
        (context(),
         polygon([(1, 1), (0.5, 1), (0.5, 0)]),
         fill("bisque")))

c7 = compose(context(),
(context(0,0.5,0.5,0.5), c5),
(context(0.5,0,0.5,0.5), c6)
)

Form と Propertyのベクトル化

FormやPropertyを生成する関数に与える引数にはベクトルを渡すことができます。以下はcircle()とfill()での例です。

using Colors
compose(context(),
        circle([0.25, 0.5, 0.75], [0.25, 0.5, 0.75], [0.1]),
        fill([LCHab(92, 10, 77), LCHab(68, 74, 192), LCHab(78, 84, 29)]))

関数の種類

ドキュメントが整備されていないため、ソースを読んで判断します。関数名から主要なものと判断したものを挙げています。

Form

• rectangle()
• polygon()
• circle()
• ellipse()
• text()
• line()
• curve()
• bitmap()
• path()

Property

• fill()
• fillopacity()
• stroke()
• strokedash()
• strokelinecap()
• strokelinejoin()
• strokeopacity()
• linewidth()
• clip()
• font()
• fontsize()
• visible()

図の保存

draw(SVG("tomato.svg", 4cm, 4cm), composition)

またCairoをインストールすればPNGやPDFでも保存することができます。図に文字が含まれている場合は、加えてPangoとFontconfigが必要になります。

応用例

Sierpinski triangle

チュートリアルに載っていた例です。

function sierpinski(n)
    if n == 0
        compose(context(), polygon([(1,1), (0,1), (1/2, 0)]))
    else
        t = sierpinski(n - 1)
        compose(context(),
                (context(1/4,   0, 1/2, 1/2), t),
                (context(  0, 1/2, 1/2, 1/2), t),
                (context(1/2, 1/2, 1/2, 1/2), t))
    end
end

composition = compose(sierpinski(6), fill("grey"))

ゲノムブラウザ

分子生物学やゲノム生物学、オミックス生物学でよく使われるツールにゲノムブラウザ (Genome browser) というものがあります。
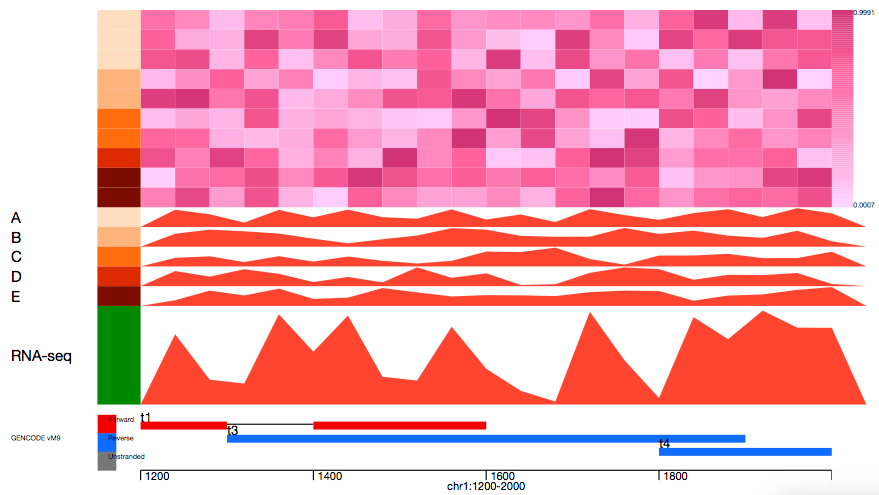
これは、横軸にゲノム上の座標、縦にゲノム上に定義される様々なデータを表現するトラックを並べたものです。
データの種類には数値データ（例：位置ごとのRNA合成量）や区間データ（例：遺伝子アノテーション）があります。

もともとRのGridパッケージでゲノムブラウザやそれに類する図を作成していたのですが、それを移植するにあたりComposeの勉強をしていました。
まだ開発途中ですが、こんな図がサクサク描けるパッケージを目指しています。

まとめ

Composeパッケージは図をどんどん入れ子にしていけるのが面白いです。
みなさんも「こんな図が作りたい」というのがあればComposeで作図関数から作ってみてはいかがでしょうか。

オマケ（配慮済み）

using Compose, Colors, Measures 


a = 1
x = 18
nSnow = 2000
xrand = rand(nSnow) .* 20 - 10
yrand = abs(randn(nSnow) .* 5)
startT = 5/8
shiftT = 5/8
heighT = 1.5
fac = 3/2

coordStar = [
(0,0),
(-a*sin(x/180*pi), a*cos(x/180*pi)),
(1/2*a, 1/2*a * tan(2*x/180*pi)),
(-1/2*a, 1/2*a * tan(2*x/180*pi)),
(a*sin(x/180*pi), a*cos(x/180*pi)),
(0,0)
]

s = compose(context(units=UnitBox(-1/2,0,1,1)), polygon(coordStar), fill("yellow"))

t = compose(context(units=UnitBox(0,0,1,1)), polygon([(1,1), (0,1), (1/2, 0)]))

compose(context(units=UnitBox(-5,0,10,10)), 
                (context(-5, 8.5, 5, 1), text(5, 0, "Merry Christmas and Happy Holidays!", hcenter, vcenter), fontsize(20pt), fill("white")),
                (context(-1/2, 0, 1, 1), s),
                (context(-1, startT, 2, heighT), t, fill("green")),
                (context(-1*fac, startT+shiftT, 2*fac ,heighT*fac), t, fill("green")),
                (context(-1*fac^2, startT+shiftT*2, 2*fac^2 ,heighT*fac^2), t, fill("green")),
                (context(-1*fac^3, startT+shiftT*3, 2*fac^3 ,heighT*fac^3), t, fill("green")),
                (context(-1/2, 2+1*3/2*3/2*3/2, 1 ,7), rectangle(), fill("brown")),
                (context(), circle(xrand, yrand, fill(0.05, nSnow)), fill("white")),
(context(-5,0,10,10), rectangle(), fill(LCHab(40,50,-70))),


)