厳密な定義や証明は略していますが、ポリトープを用いて不確かなモデルを表現し、その安定性を状態フィードバック則を用いて考えています。凸結合やポリトープについての簡単なまとめはこちらです。
不確かなプラントのポリトープ表現
具体例
不確かなプラントの数式表現方法について以下の具体例を用いて考える。
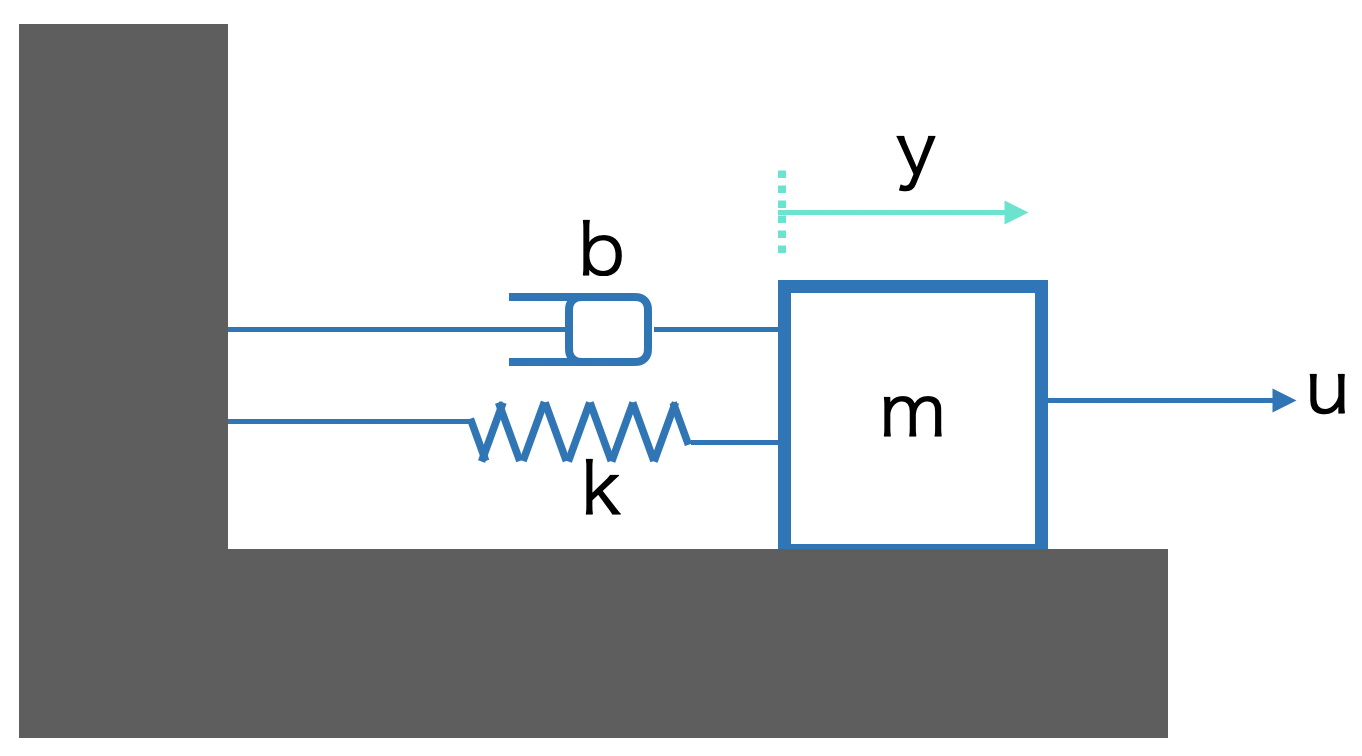
上図のマス・バネ・ダンパー系($y(t)$をマスの変位,$m$をその質量,$b$をダンパーの粘性摩擦係数,$u(t)$を外力とする)について、状態変数を$x=\begin{bmatrix}
y & \dot{y}
\end{bmatrix}^T$とする状態方程式で表すと
\dot{x}=\begin{bmatrix}
0 & 1\\
-\frac{k}{m} & -\frac{b}{m}
\end{bmatrix}x+\begin{bmatrix}
0 \\
\frac{1}{m}
\end{bmatrix}u
\tag{1}
となる。ただし、各パラメータ$m,b$は不確かで
m_1\le m\le m_2,~~~~b_1\le b\le b_2
\tag{2}
であるとする。ここで、パラメータの逆数である$\frac{1}{m}$や除算である$\frac{b}{m}$が各頂点の凸結合($\alpha_1,\alpha_2,\beta_1,\beta_2\ge 0,\alpha_1+\alpha_2=1,\beta_1+\beta_2=1$を用いる)で表現できるかを確かめると、
\begin{align}
\frac{1}{m}&=(\beta_1+\beta_2)(\alpha_1\frac{1}{m_1}+\alpha_2\frac{1}{m_2})\\
&=\alpha_1\beta_1\frac{1}{m_1}+\alpha_1\beta_2\frac{1}{m_1}+\alpha_2\beta_1\frac{1}{m_2}+\alpha_2\beta_2\frac{1}{m_2}
\end{align}
\tag{3}
\begin{align}
\frac{b}{m}&=(\beta_1b_1+\beta_2b_2)(\alpha_1\frac{1}{m_1}+\alpha_2\frac{1}{m_2})\\
&=\alpha_1\beta_1\frac{b_1}{m_1}+\alpha_1\beta_2\frac{b_2}{m_1}+\alpha_2\beta_1\frac{b_1}{m_2}+\alpha_2\beta_2\frac{b_2}{m_2}
\end{align}
\tag{4}
\begin{align}
\alpha_1\beta_1+\alpha_1\beta_2+\alpha_2\beta_1+\alpha_2\beta_2&=\alpha_1(\beta_1+\beta_2)+\alpha_2(\beta_1+\beta_2)\\
&=\alpha_1+\alpha_2=1
\end{align}
\tag{5}
と変形できる。よって、パラメータの逆数・除算・(積)はすべて各頂点の凸結合で記述できることがわかる。以上より、ダイナミクス(1)の係数行列を左から$A(m,b),B(m,b)$として、行列ポリトープを用いて表現すると
\begin{align}
A(m,b)&=\lambda_1A(m_1,b_1)+\lambda_2A(m_1,b_2)+\lambda_3A(m_2,b_1)+\lambda_4A(m_2,b_2)\\
B(m,b)&=\lambda_1B(m_1,b_1)+\lambda_2B(m_1,b_2)+\lambda_3B(m_2,b_1)+\lambda_4B(m_2,b_2)\\
&\lambda_1,\lambda_2,\lambda_3,\lambda_4\ge 0,~~~\lambda_1+\lambda_2+\lambda_3+\lambda_4=1,
\end{align}
\tag{6}
と記述できる。ただし、パラメータの冪乗(例えば、$m^2$など)は
m^2=(\alpha_1m_1+\alpha_2m_2)^2=\alpha_1^2m_1^2+2\alpha_1\alpha_2m_1m_2+\alpha_2^2m_2^2
\tag{7}
のように交差積$m_1m_2$が存在し、各頂点の冪乗$m_1^2,m_2^2$の凸結合で明らかに表現することができないので、行列ポリトープで表現することもできない。
まとめ
上記の具体例を一般化してまとめると、不確かなベクトル$\theta$を持つシステム$(A(\theta),B(\theta),C(\theta))$は、パラメータの各頂点$\theta_i$が既知であり、その頂点が$N$個であるとすると
\left\{
\begin{array}{rl}
\dot{x} & = \bigl\{\Sigma_{i=1}^N\lambda_iA(\theta_i)\bigr\}x+\bigl\{ \Sigma_{i=1}^N\lambda_iB(\theta_i)\bigr\}u\\
y & = \bigl\{\Sigma_{i=1}^N\lambda_iC(\theta_i)\bigr\}x\\
\lambda_i&\ge 0,~~~\Sigma_{i=1}^N\lambda_i=1
\end{array}
\right.
\tag{8}
二次安定性(状態フィードバック則を設計)
プラント集合全てに対して、一つの二次関数$V=x^T Px$($P\succ0$)を用いてプラント集合の安定性を示すことができる場合、プラント集合は二次安定(quadratically stable)という。
ここでは、不確かなパラメータを持つプラント集合であるポリトープ系$(A(\theta),B(\theta),C(\theta))$を二次安定化する状態フィードバック則を考える。つまり、
\left\{
\begin{array}{rl}
\dot{x} & = \bigl\{\Sigma_{i=1}^N\lambda_iA_i\bigr\}x+\bigl\{ \Sigma_{i=1}^N\lambda_iB_i\bigr\}u\\
u&=Kx\\
\lambda_i&\ge 0,~~~\Sigma_{i=1}^N\lambda_i=1
\end{array}
\right.
\tag{9}
の$K$を設計する。(簡単のため、式(8)に関して$A(\theta_i)$を$A_i$,$B(\theta_i)$を$B_i$とした。)この時、閉ループ系は
\begin{align}
\dot{x}&=\Sigma_{i=1}^N\lambda_i(A_i+B_iK)x\\
\lambda_i&\ge 0,~~~\Sigma_{i=1}^N\lambda_i=1
\end{align}
\tag{10}
となる。ここで、二次関数$V=x^TPx$に関して、
\begin{align}
\dot{V}&=[\Sigma_{i=1}^N\lambda_i(A_i+B_iK)x]^TPx+x^TP[\Sigma_{i=1}^N\lambda_i(A_i+B_iK)x]\\
&=x^T[\Sigma_{i=1}^N\lambda_i\bigl\{(A_i+B_iK)^TP+P(A_i+B_iK)\bigr\}]x
\end{align}
\tag{11}
とであることから、$\lambda_i\ge 0,~\Sigma_{i=1}^N\lambda_i=1$より、
\begin{align}
&(A_i+B_iK)^TP+P(A_i+B_iK)< 0\\
\Leftrightarrow & A_i^TP+PA_i+(B_iK)^TP+PB_iK< 0
~~~\forall i=1,\ldots,N
\end{align}
\tag{12}
を満たすゲイン$K$と$P\succ0$が存在すれば、閉ループ系(10)は二次安定である。ただし、双線形項$(B_iK)^TP,PB_iK$を含んでいるのでNP困難である。そこで、式(12)の両辺に左右から$Q=P^{-1}$をかけて変形すると、
\begin{align}
&QA_i^T+A_iQ+(KQ)^TB_i^T+B_i(KQ)<0\\
\Leftrightarrow & QA_i^T+A_iQ+X^TB_i^T+B_iX<0
~~~\forall i=1,\ldots,N
\end{align}
\tag{13}
と整理されるので、変数行列(Q,X)に関する線形行列不等式として計算することが簡単となった。ただし、$X=KQ$とおいた。よって、式(13)の数値計算を行い(Q,X)が決まれば、$K=XQ^{-1}$よりフィードバック制御則を設計することができる。
参考文献
[1]Lyapunov methods in robustness—an overview,Franco Blanchini,Dipartimento di Matematica,e Informatica,Universit`a di Udine,33100 Udine, Italy,03/June/2016
[2]S. Boyd, L. El Ghaoui, E. Feron, and V. Balakrishnan, Linear Matrix Inequalities in System and Control Theory. SIAM Press,
1994.