Juliaで古典アニーリングマシンを実装する #画像処理

前回の記事で，古典アニーリングのアルゴリズムについて導入しました．本記事では，その実装を行います．対応する著者のgithubリンクはこちらからどうぞ！

概要 & 環境

数値計算特化言語であるJuliaを用いて，古典アニーリングマシンを実装し，応用例として画像のノイズ除去を行います．使用するライブラリ一覧は以下の通りです．

Julia >= v1.6.1
StatsBase >= v0.33.13
MLDatasets == v0.5.14
ImageView == v0.10.15

アルゴリズム

前回の記事より，シミュレーティッド・アニーリング(SA)のアルゴリズムは以下のようになるのでした．今回はMetroPolis法を主として実装を行います．


SA-ALGO.

アニーリングサンプラーの実装

1. 構造体定義

今回のコーディングでは，ハミルトニアンの算出部分で行列演算を用いるので，線形代数のライブラリを使用します．また，アルゴリズム中の過程でランダムにスピンを一つ選んで反転させる操作が必要なため，StatsBaseライブラリのsample()関数を使用します．

sampler.jl

using LinearAlgebra
import StatsBase.sample

次に，アニーリングの結果として返される構造体を構築します．前回の記事より，ハミルトニアンの一般系は

\begin{align*}
\mathcal{H}=-\sum_{i=1}^Nb_i\sigma_i-\sum_{i<j}w_{ij}\sigma_i\sigma_j
\end{align*}

でした．$\ i<j\,$はスピン間相互作用の寄与を2回重複して数えないようにするための条件です．

ハミルトニアン中の磁場$\, b_i$と相互作用$\, w_{ij}$を構造体の内部で保持するようにします．構造体は以下のように定義します．(sampler.jlファイルに書き込みます)

sampler.jl

mutable struct Response{T, I}
    W::Matrix{T} # 相互作用行列
    b::Matrix{T} # 磁場行列
    states::Vector{Vector{I}}　# 1アニーリングごとに最適なスピン状態を保持
    energies::Vector{T} # 1アニーリングごとにエネルギーの最低値を保存
    indices::Vector # スピン変数についている名前(ラベル)を保持
    sample::Dict # 複数回のアニーリングで，エネルギー最低時のスピン状態を保存
end

この構造体を初期化する関数も定義しておきます．先ほどの構造体に具体的な属性を与える形で定義します．「n_unit」はスピンの総数です．

sampler.jl

function Response(n_unit::Int64)
    Response{Float64, Int64}(
        rand(n_unit, n_unit),
        rand(n_unit, 1),
        Vector{Vector}[],
        [],
        [],
        Dict()
    )
end

構造体中の相互作用$\,w_{ij}$行列及び，磁場$\,b_i$行列はrand()関数で乱数行列をもって初期化しておきます．この要素はユーザーが設定した値で後に書き換えることになります．

2. スピンのラベリング

入力されたスピン変数のラベルを整数番号に付けかえる関数を作成します．今回の仕様では，例えば２つのスピン変数$\,a,b\in\{+1, -1\}$間に相互作用$\,w_{ab}=-1$を設定するとき，

julia> w = Dict(("a", "b") => -1)

と辞書入力することを仮定しています．しかし，実際に内部で扱う際には文字列のラベルより数字で通し番号をつけた方が管理しやすいため，

のように，スピン変数名を整数番号に変換するわけです．ソースコードは以下のようになります．

sampler.jl

function relabel_dict(key_lst::Vector, linear::AbstractDict, 
                      quad::AbstractDict)

    num_nodes = collect(1:length(key_lst))
    tab = Dict(zip(sort(key_lst), num_nodes))
    bias, interact = Dict(), Dict()

    for key in keys(quad)
        key1, key2 = key
        interact[(tab[key1], tab[key2])] = quad[key]
    end

    for key in keys(linear)
        bias[tab[key]] = linear[key]
    end

    return bias, interact
end

3. 構造体の生成

1.で定義したアニーリングの結果を保持する構造体Responseを生成する関数も用意しておきます．磁場の入力「linear」と相互作用の入力「quad」を受け付けて，そこからスピン変数の集合「key_list」を求めます．スピン変数の集合の要素数＝スピン数なので，スピン数をResponse構造体に渡して初期化します．

sampler.jl

function create_response(linear::AbstractDict, quad::AbstractDict)

    # fetch key list
    Jkeys = collect.(keys(quad))
    key_list = collect(Set(vcat(keys(linear)..., Jkeys...)))
    sort!(key_list)
    linear, quad = relabel_dict(key_list, linear, quad)

    # create field & response
    n_unit = length(key_list)
    resp = Response(n_unit)
    field = zeros((n_unit, 1))
    field[collect(keys(linear))] .= values(linear)

    copy!(resp.W, trans(quad, n_unit))
    copy!(resp.b, field)
    resp.indices = key_list
    return resp
end

途中で出てきた「trans()」関数は辞書⇒行列の変換関数です．sampler.jl内に関数を定義します．

trans関数のソースコード

sampler.jl

function trans(dict::AbstractDict, len::Int64)

    arr = zeros((len, len))
    for (key, val) in zip(keys(dict), values(dict))
        arr[key...]  = val
        arr[reverse(key)...] = val # symmetric
    end
    return arr
end

trans()関数は，要素のインデックス$\,(i,j)\,$をキーに持つ辞書を行列に変換する効果を持ちます．入力として，3つのスピンを仮定しtrans()によって行列を生成する例を以下に示します．

julia> J = Dict((1, 2) => 100, (2, 3) => -500);

julia> trans(J, 3) # 1行2列に100，2行3列に-500をもつ3×3の対称行列
3×3 Matrix{Float64}:
   0.0   100.0     0.0
 100.0     0.0  -500.0
   0.0  -500.0     0.0

4. MetroPolis法に必要な関数群

MetroPolisアルゴリズムでは，以下のステップを必要とするのでした．

ランダムにスピンを一つ選び反転する(シングルスピンフリップ)．
スピン反転を行う前と後でエネルギーの差分を計算する．
2.の情報をもとに受容率$A$を計算する．

\begin{equation*}
A=\mathrm{min}\left(1,\ e^{-\beta\,[\,\mathcal{H}(-\sigma_k)-\mathcal{H}(\sigma_k)\,]}\right)
\end{equation*}

ここでは，以上の3つの機能を有する関数を構築していきます．

4.1. シングルスピンフリップ

スピンの値$\,\pm1\,$を保有する「state」ベクトルのうち，ランダムに一つスピンを選んで反転する関数です．何番目のスピンをフリップさせたかのインデックスを返します．

sampler.jl

function spin_flip!(state::Vector)
    idx = sample(1:length(state), 1)
    state[idx] *= -1 # single spin flip
    return idx
end

「spin_flip!」関数では，下図のように乱択された一つのスピン変数の符号を入れ替えることで反転操作を行います．このスピン変数を集めたベクトル$\,\boldsymbol{\sigma}\,$はプログラム内の「state」ベクトルに対応します．

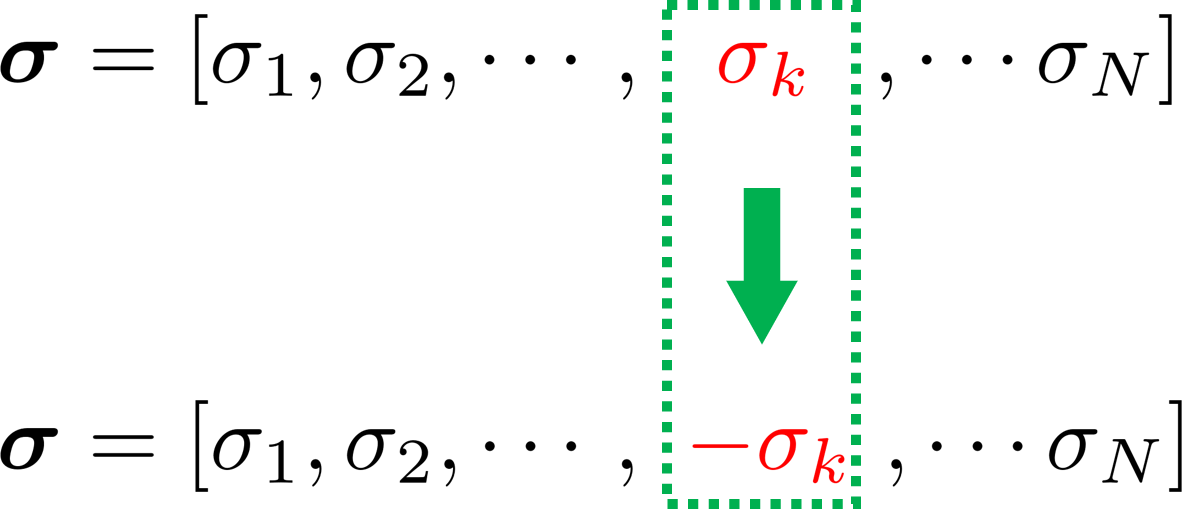
4.2. エネルギーの計算

ハミルトニアンの値を具体的に計算する部分です．イジングハミルトニアンは

\begin{align*}
\mathcal{H}=-\sum_{i}b_i\sigma_i-\sum_{i<j}w_{ij}\sigma_i\sigma_j
\end{align*}

ですが，これは次のように2次形式で行列表現した場合と等価です．

\begin{align*}
\mathcal{H}=-\boldsymbol{b}\cdot\boldsymbol{\sigma}-\frac{1}{2}\boldsymbol{\sigma}^\mathrm{T}\boldsymbol{\mathrm{W}}\boldsymbol{\sigma}
\end{align*}

ここで，$\ \boldsymbol{b}^\mathrm{T}=[\,b_1,\cdots,b_N\,]\,$は磁場パラメータを集めたベクトルで，相互作用行列$\,\boldsymbol{\mathrm{W}}$は$w_{ij}$を要素にもつ行列です．数式をそのまま入力する形で実装できます．

sampler.jl

function get_energy(resp::Response{T}, state::Vector) where T
    E = -dot(vec(resp.b), vec(state)) # linear term
    E -= state' * triu(resp.W, 1) * state * 0.5 # interaction term
    return E
end

4.3. 受容率

スピン反転を確定するかどうかを決める受容率の計算部分です．MetroPolis法の中核になります．

sampler.jl

function accept_rate(dE::T, beta::T) where T
    return min(1, exp(-beta * dE))
end

5. サンプリング関数(MetroPolis法)

最後に，古典アニーリング実行関数を作成します．参考のため，MetroPolis法のアルゴリズムを以下に再掲しておきます．

ソースコードは以下のようになります．
逆温度を「beta_min」から「beta_max」まで少しずつ上げながら，アニーリングステップを順次実行します．「num_reads」パラメータはアニーリングを何回行うかを指定する変数です．

sampler.jl

function anneal(linear::AbstractDict, quad::AbstractDict;
    num_sweeps::Integer = 1000, num_reads::Integer = 100,
    beta_min::Real = 0.0, beta_max::Real = 10.0)

    resp = create_response(linear, quad)
    state = ones(size(resp.W, 1))
    energy = zero(eltype(resp.W))

    for step in 1:num_reads
        @simd for beta in range(beta_min, beta_max, length = num_sweeps)

            # random spin flip
            idx = spin_flip!(state)

            # check energy level
            new_energy = get_energy(resp, state)
            dE = new_energy - energy

            # MetroPolis algorithm
            if rand() < accept_rate(dE, beta)
                energy = new_energy
            else
                state[idx] *= -1
            end
        end

        # append some info
        push!(resp.states, Int.(state))
        push!(resp.energies, energy)

    end
    optimal_idx = argmin(resp.energies)
    resp.sample = Dict(zip(resp.indices, resp.states[optimal_idx]))
    return resp

end

ソースコード全体

sampler.jlのソースコード全体をまとめます．

ソースコード全体

sampler.jl

using LinearAlgebra
import StatsBase.sample


mutable struct Response{T, I}
    W::Matrix{T}
    b::Matrix{T}
    states::Vector{Vector{I}}
    energies::Vector{T}
    indices::Vector
    sample::Dict
end


function Response(n_unit::Int64)
    Response{Float64, Int64}(
        rand(n_unit, n_unit),
        rand(n_unit, 1),
        Vector{Vector}[],
        [],
        [],
        Dict()
    )
end


# initial setting
function create_response(linear::AbstractDict, quad::AbstractDict)

    # fetch key list
    Jkeys = collect.(keys(quad))
    key_list = collect(Set(vcat(keys(linear)..., Jkeys...)))
    sort!(key_list)
    linear, quad = relabel_dict(key_list, linear, quad)

    # create field & response
    n_unit = length(key_list)
    resp = Response(n_unit)
    field = zeros((n_unit, 1))
    field[collect(keys(linear))] .= values(linear)

    copy!(resp.W, trans(quad, n_unit))
    copy!(resp.b, field)
    resp.indices = key_list
    return resp
end


function trans(dict::AbstractDict, len::Int64)

    arr = zeros((len, len))
    for (key, val) in zip(keys(dict), values(dict))
        arr[key...]  = val
        arr[reverse(key)...] = val # symmetric
    end
    return arr
end


function relabel_dict(key_lst::Vector, linear::AbstractDict, quad::AbstractDict)

    num_nodes = collect(1:length(key_lst))
    tab = Dict(zip(sort(key_lst), num_nodes))
    bias, interact = Dict(), Dict()

    for key in keys(quad)
        key1, key2 = key
        interact[(tab[key1], tab[key2])] = quad[key]
    end

    for key in keys(linear)
        bias[tab[key]] = linear[key]
    end

    return bias, interact
end


# annealing algorithm
function get_energy(resp::Response{T}, state::Vector) where T
    E = -dot(vec(resp.b), vec(state)) # linear term
    E -= state' * triu(resp.W, 1) * state * 0.5 # interaction term
    return E
end


function accept_rate(dE::T, beta::T) where T
    return min(1, exp(-beta * dE))
end


function spin_flip!(state::Vector)
    idx = sample(1:length(state), 1)
    state[idx] *= -1 # single spin flip
    return idx
end


# sampling function
function anneal(linear::AbstractDict, quad::AbstractDict;
    num_sweeps::Integer = 1000, num_reads::Integer = 100,
    beta_min::Real = 0.0, beta_max::Real = 10.0)

    resp = create_response(linear, quad)
    state = ones(size(resp.W, 1))
    energy = zero(eltype(resp.W))

    for step in 1:num_reads
        @simd for beta in range(beta_min, beta_max, length = num_sweeps)


            # random spin flip
            idx = spin_flip!(state)

            # check energy level
            new_energy = get_energy(resp, state)
            dE = new_energy - energy

            # MetroPolis algorithm
            if rand() < accept_rate(dE, beta)
                energy = new_energy
            else
                state[idx] *= -1
            end
        end

        # append some info
        push!(resp.states, Int.(state))
        push!(resp.energies, energy)

    end
    optimal_idx = argmin(resp.energies)
    resp.sample = Dict(zip(resp.indices, resp.states[optimal_idx]))
    return resp

end

テスト

次の画像のような設定を考えます．

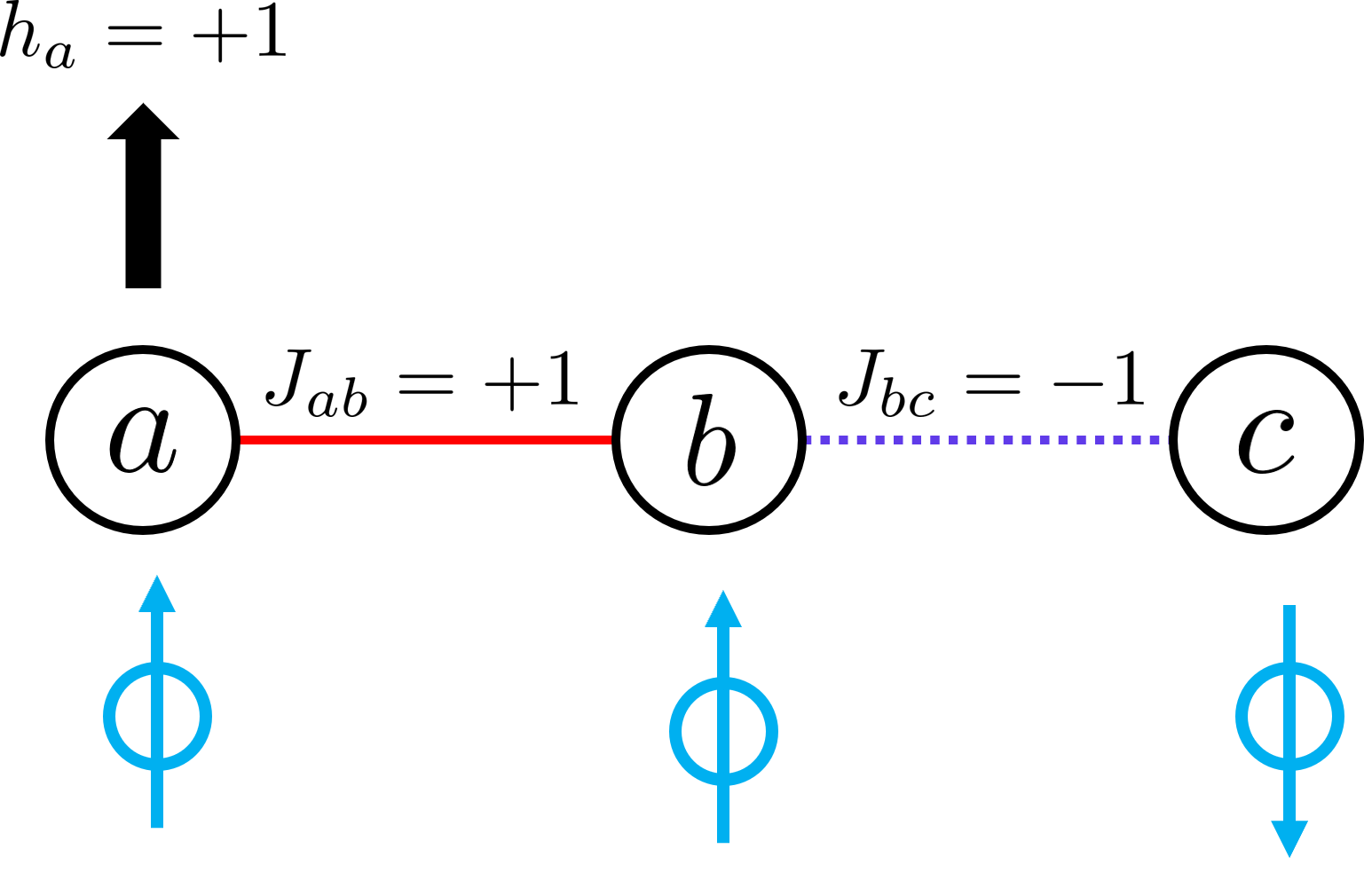
前回の記事と同様に$\ (a,b,c)=(\,+1,+1,-1\,)\,$が基底状態です．作成した「sampler.jl」ファイルがあるフォルダ内でjuliaを起動し，アニーリングによってこの基底状態が求められるかテストします．

julia> include("./sampler.jl")

julia> h = Dict(:a => +1);

julia> J = Dict((:a, :b) => +1, (:b, :c) => -1);

julia> result = anneal(h, J);

julia> result.sample
Dict{Symbol, Int64} with 3 entries:
  :a => 1
  :b => 1
  :c => -1

確かにMetroPolis法を用いたアニーリングによって，基底状態を求められていることが確認できました！

応用

アニーリングの応用例としてこちらの記事を参考に，画像のノイズ除去を試行してみました．

概念図を以下に載せます．ノイズの付与された$\ i\,$番目のピクセル値$\ h_i\in\{+1,-1\}\,$の情報から，ノイズのない未知変数$\,\sigma_i\,$をアニーリングによって最適化し，ノイズ除去を行います．

$\,h_i,\sigma_i\,$の間には相関があるため，$\,h_i,\sigma_i\,$が同符号の時にエネルギーが低くなるようにハミルトニアンを構築します．また，隣り合う画素間にも「同じピクセル値をとりやすい」という相関があるため，これらの情報をハミルトニアンに組み込むと

\begin{align*}
&\mathcal{H}=-\eta\sum_ih_i\sigma_i-\beta\sum_{i,j}\sigma_i\sigma_j
\end{align*}

と構築されます．これは，イジングハミルトニアンと同形になるので，本記事で作成したアニーリングサンプラーをそのまま適用することができます．「sampler.jl」ファイルが存在するディレクトリ内に，以下の「imtest.jl」を作成します．

【imtest.jl】画像ノイズ除去のソースコード

imtest.jl

using MLDatasets
using ImageView
using StatsBase
include("./sampler.jl")


function get_data(;idx::Int64=1)
    # MNIST画像の取得
    Xtrain, ytrain = MNIST.traindata(Float32)
    X = transpose(Xtrain[:, :, idx]) .< 0.5
    return X
end


function add_noise(img::BitMatrix, weight::Float64 = 0.03)
    # ノイズ付加
    bit_vec = sample(0:1, Weights([weight, 1 - weight]), length(img))
    noised = img .* reshape(bit_vec, size(img))
    return noised
end


function get_params(noised_img::Matrix; eta::Float64 = 1.0, beta::Float64 = 1.0)

    # アニーリングに用いる磁場，相互作用パラメータ設定
    J = Dict()
    h = Dict(zip(collect(1:length(noised_img)), eta * (2 .* noised_img[:] .- 1)))
    getid(x, y) = reshape(1:length(noised_img), size(noised_img))[x, y]

    num_edge = size(noised_img)[1] - 1
    for x = 1:num_edge, y = 1:num_edge

        J[(getid(x, y), getid(x + 1, y))] = beta
        J[(getid(x, y), getid(x, y + 1))] = beta

    end
    return h, J
end


# 画像表示
img = get_data()
noised_img = add_noise(img)
imshow(img; canvassize=(400, 400));
imshow(noised_img; canvassize=(400, 400))

# アニーリングによるノイズ除去
h, J = get_params(noised_img, eta = 1.5, beta = 1.51)
resp = anneal(h, J, num_reads = 50)
processed_img = reshape(collect(values(sort(resp.sample))), size(img))
imshow(processed_img; canvassize=(400, 400))

imtest.jlを実行すると，結果は以下のようになりました．

原画像	ノイズ付与後	アニーリング適用後

これを見ると，初期状態と同程度まで復元できていることが分かります．ソースコード中のアニーリング回数「num_reads」や，逆温度の刻み幅「num_sweeps」パラメータなどのハイパーパラメータを適切な値にすることで，さらに精度よく復元できるはずです！

まとめ

本記事で，古典アニーリングマシンをJulia言語を用いて実装しました．
また，応用例としてアニーリングによる画像のノイズ除去を行いました．

Juliaで古典アニーリングマシンを実装する

概要 & 環境

アルゴリズム

アニーリングサンプラーの実装

1. 構造体定義

2. スピンのラベリング

3. 構造体の生成

4. MetroPolis法に必要な関数群

4.1. シングルスピンフリップ

4.2. エネルギーの計算

4.3. 受容率

5. サンプリング関数(MetroPolis法)

ソースコード全体

テスト

応用

まとめ

参考文献