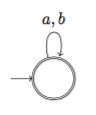隠された正規言語を見つけ出す（Angluinのアルゴリズム）

問題設定

「計算論的学習理論」の界隈で「有限オートマトンの学習」と呼ばれる問題を考えます。

隠し情報（当てたいこと）

$\Sigma^*$上の正規言語 $T$ が隠されているので、これを対話によって当てたい。実際には$T$を受理するDFAや、正規表現が隠されていると思って良い。

（注意: $T$ は隠されているが、有限アルファベット$\Sigma$は隠されてはいない)

$T$に関して許される操作

所属性質問 $ \textbf{Mem}(w) $

文字列 $w \in \Sigma^*$ が $T$ に入っているかどうかを教えてもらうことはできる。

等価性質問 $ \textbf{Eq}(A) $

手元にオートマトン $A$ があるなら、$L(A) = T$ となっているかどうかを調べることができる。 $L(A) = T$の場合にはyesが返り、 そうでない場合は $(L(A) \setminus T) \cup (T \setminus L(A))$の要素が一つ返ってくる。

例題

正規表現 $ T = a^* b^* $ が隠されている状況で、ユーザーは所属性質問と等価性質問だけで、それ以外のヒントは何もなしに、$ T = a^* b^* $ をあてます。

まず以下のようなオートマトン $A_1$ を何も考えずに作ってみて:

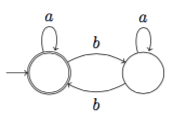
このオートマトン$A_1$と$T$が等しいかどうかを、等価性質問 $\textbf{Eq}(A_1)$ によって調べます。 $L(A_1) = \\{a,b\\}^* $、つまり $A_1$ は $a, b$ からなるどんな文字列をも受理するため $T$ と等価でないことが分かり、例えば $\textbf{Eq}(A_1) = ba \in L(A_1) \setminus T$ が返ってきます。

またしても何も考えずに次のオートマトン $A_2$ を作ってみます:

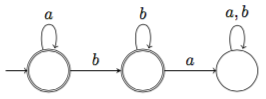
$ L(A_2) = ( a^* b a^* b )^* $ ですので、等価性質問 $\textbf{Eq}(A_2)$ を行うと、またしても$T$とは等価ではないことが分かり、例えば $ \textbf{Eq}(A_2) = ab \in T \setminus L(A_2)$ が返ってきます。

諦めずに何も考えずに次のオートマトン $A_3$ を作ってみます:

$A_3$ は、$ a^* b^* $を受理するオートマトンで、等価性質問 $\textbf{Eq}(A_3)$ を行うと *yes* が得られ、隠された$T$が実は$ T = a^* b^* $ であることが分かりました。

ここでは具体的な正規言語を固定して考えてみましたが、一般にはどのようにすれば、隠された$T$をあてることができるでしょうか。

素朴な戦略（全列挙アルゴリズム）

最も素朴な方法として、状態数の小さい方からオートマトンを全列挙していく方法があります。
すなわち

• 状態数1のDFAを全て生成し、等価性質問をその全てについて行い、どれかでyesが返ってきたならばそれが答え。
• 余談ですが、状態数1のDFAは、 $\Sigma^*$ を受理するものと、空集合 $ \emptyset $ を受理するもの、二つだけです。
• 状態数1のDFAではyesが得られなかった場合は、状態数2のDFAを 全て 生成し、等価性質問を片っ端から行う。
• 今度は状態数3で…としてこの処理を繰り返すと、いつかは$T$にぶち当たる。

従って、この問題は、解けるかどうかでいえば「解ける」ということになります。
ただし、この方法では「いつかは計算が止まる」ことは分かるものの、いつ止まるのか全く見通しが立っていません。

全列挙アルゴリズムはどれくらいの時間がかかる?

「いつかは計算が止まる」ではお粗末すぎるので、もう少し、計算に必要な時間を見積りたいと思います。そのために、正規言語$L$が与えられたときの「サイズ」を定義します。

正規言語の難しさを表すような指標には種類があるのですが、ここでは

\text{size}(L) = \min \bigl\{ \mathcal{A}\text{の状態数}\ : \text{$\mathcal{A}$ はDFAで $L(\mathcal{A}) = L$とする} \bigr\}

として定義します。
$\text{size}(L)$は、$L$をDFAによって受理するのに必要になる状態数を意味しています。必要になる状態数が多ければ多いほど、その正規言語は難しい何かを表現しているのではないか？と考えるのは、それほど不自然ではありません。

「必要状態数」によって「サイズ」を表すこととすると、「隠された正規言語のサイズ」を$N$とした時に、上のアルゴリズムが停止するまでにどれくらいの時間が必要になるでしょうか。これは状態数 $N$ のDFAの総数が幾つかという話になり、アルファベット $\Sigma$ のサイズに依存しますが、仮に$\Sigma = { a }$の場合に限っても$2^N$を超えてきます。

この話に個別に興味のある方は

• Michael Domaratzkiの Enumeration of Formal Languages http://www.cs.umanitoba.ca/~mdomarat/pubs/efl.pdf
• Michael Domaratzkiらによる On the number of distinct languages accepted by finite automata with n states http://dl.acm.org/citation.cfm?id=782472
  も面白いかと思います。

ということで、正規言語のサイズ$N$に関して$2^N$回程度（実際には$2^N$回より非常に大きいと思って良い）の「等価性質問」を行うことになります。「所属性質問」と「等価性質問」に実際にどれくらい時間がかかるかはここでは避けることにして、解けるには解けますが時間がかかりすぎで、心もとないです。もう少しなんとかならないのでしょうか。

効率よく解くことはできるか?

$T$のサイズ$N = \text{size}(T)$について、$N$に関して多項式回程度$O(\text{poly}(N))$の「質問」で解くことができれば、「効率的に」解けていると思うことにしましょう。
多項式回で効率的…？というのももっともな意見ですが、上のアルゴリズムよりはまともそうですし、ここでは効率的だと思うことにして頂いて……

上のアルゴリズムでは「等価性質問」だけを連打することで解決を図っていました。

一方で、

{\rm\large 所属性質問と等価性質問を組み合わせると}  {\Large O(\text{poly}(N))}  {\rm\large 回の質問で} {\Large T } {\rm\large をあてられる}

という結果が、以下のAngluinの1987年の論文で示されています:

• Dana Angluin, Learning regular sets from queries and counterexamples, Information and Computation 1987, http://www.sciencedirect.com/science/article/pii/0890540187900526

予告

次回以降で、Angluinのアルゴリズムの内容、すなわち、どのようにすれば多項式サイズ程度回数の質問で済ませられるか、を述べます。ただ、いきなりAngluinのアルゴリズムを説明するのは骨が折れるので、Angluinのアルゴリズムで使われている道具を先に全て説明してしまいます。
具体的には、決定性有限オートマトンの最小化で使われる「同値類」や「商集合」の概念の説明を避けられません。これはどちらかというと有限オートマトン一般の話ですが、次はこれについて書きたいと思います。