目次
・はじめに
・コンピュータの中身を知る
・電気の話
・2進数の話
・論理代数
・機械語
・デコーダ
・最後に
はじめに
現在では高級言語を使ったプログラミングが主流となっています。
高級言語とは、「Java」や「Python」などに代表される、人間にとって読み書きしやすいプログラミング言語のことです。
しかしこれらの言語をコンピュータが直接解釈するわけではなく、内部でコンピュータが解釈可能な「機械語」という形に翻訳されてから処理が実行されます。
つまり高級言語で書かれたソースコードは、機械語に翻訳され、その機械語をコンピュータが読み取って動くわけですが、近年ではこれらを全く知らずとも開発が可能になってきました。
悪く言えばコンピュータの中身がブラックボックス化してきており、ソースコードによってコンピュータに命令をしているが、肝心のコンピュータがどのように動いているのかを知らないという人が増えました。
本記事ではそんなブラックボックス化したコンピュータの中身について、個人的に勉強した内容をまとめました。
仰々しいタイトルですが、あまり大したことは書いていません。コンピュータを理解するための一助となるような軽い読み物だと思って下さい。
よくあるコンピュータアーキテクチャの本の内容を焼き直しても仕方がないので、少し毛色の異なった感じになっています。
コンピュータの中身を知る
現代社会ではほとんど全ての人がコンピュータを使用しており、仕事のデスクにはパソコンが乗っているし、スマホを使ってLINEをしたり、SNSを見たりしています。家にはテレビやエアコンなどの家電があります。
(パソコンだけをコンピュータと思っている方がいるかもしれませんが、スマホや家電も立派なコンピュータです。https://toragi.cqpub.co.jp/Portals/0/backnumber/2008/04/p102-103.pdf)
これだけ多くの人がコンピュータを使用しているにも関わらず、コンピュータの中身がブラックボックス化している理由は何でしょうか。
あくまで個人的な見解ですが、その理由の一つとして、コンピュータの中を実際に開けて見たことがないせいで、内部で何が起こっているのかイメージが湧きにくいということが考えられます。
そこでまずは、パソコンの内部構造がどうなっているかを知ることで、コンピュータへのイメージを膨らましていこうと思います。
とはいえ、実際に中を開けて見て下さいと言われても困ると思うので、パソコンの中身を詳しく図解したサイトをご紹介します。
情報機器と情報の仕組み素材集
http://www.sugilab.net/jk/joho-kiki/index-sample.html
このサイトについて (著作権に関する記述を含む)
本サイトは、文部科学省が実施した平成13年度「教育用コンテンツ開発事業」により、「情報機器と情報社会のしくみ」開発委員会により制作され、同、平成14年度「教育用コンテンツ開発・改善・普及に関わる研究事業」 (いづれも主査:永野和男 聖心女子大学教授)により普及活動が行われています。
このサイトはコンピュータの中で何が起きているのかを知るのに大変役立ちました。特に動画による解説がありがたかったです。興味がある方は是非サイトをじっくり見て下さい。
コンピュータとは言うなれば巨大な電気回路であり、キーボードの打鍵やマウスクリックなどの物理的な刺激により通電し、電気信号が流れ、回路に流れる電気信号を検知して決められた動きをします。
それでは、コンピュータを動かす原動力であり、現代の生活には欠かすことのできない「電気」というものの正体を改めて見ていきたいと思います。
電気の話
電気とは何でしょうか。
電気の正体とは、一言で言えば「自由電子の運動が引き起こす様々な現象の総称」です。
原子の話から順を追って説明していきます。
全ての物質は原子から出来ており、原子は原子核とその周りを回る電子で構成されています。
さらに原子核は陽子と中性子に分けることができます。
陽子は+の電荷を、電子は−の電荷を持ちます。(中性子は電荷を持ちません。)
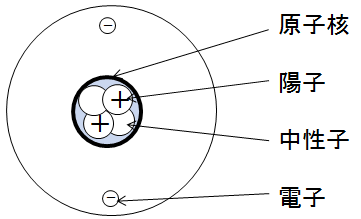
+の電荷と−の電荷の間には引き付け合う力が働きます。(これは電磁気力という、電気を帯びた粒子にはたらく力によるものです。)
原子核の陽子の個数=原子番号であり、原子核の周りには陽子と同じ個数の電子が回っています。
陽子の数は変わりませんが、原子核の周りを飛んでいる電子の数は変わることがあります。原子は電子を放出したり受け取ったりすることができるのです。
原子核から離れて自由に動くことができるようになった電子を自由電子と呼びます。この自由電子が、様々な電気による現象を引き起こす主役となります。
原子が自由電子を放出する(あるいは受け取る)理由についても少し触れておきましょう。
原子にはイオン化エネルギーというものがあり、これが高いほど安定した状態にあります。
イオン化エネルギーが高い原子というのは主に周期表の右側、つまりK殻やL殻の軌道に電子が満たされた状態の原子です。
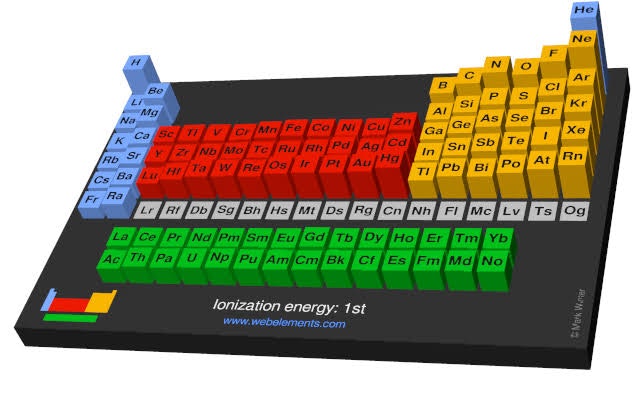
エネルギー的に不安定な原子は、より安定した構造を取りたいために電子の授受を行うという理屈です。
例えばMgであれば、K殻に2個、L殻に8個、M殻に2個という電子配置をしています。表を見れば分かるように、Mgはイオン化エネルギーが低い、即ち安定していないため、M殻にある余分な電子2個を放出して、安定した原子であるNeと同じ構造を取ろうとします。
この時放出された2個の電子が自由電子として、原子核を離れて動き回れるようになるというわけです。
電気の基本的な単位である、「電流」、「電圧」、「電気抵抗」についても復習しておきましょう。これらは中学校で習ったオームの法則に登場する単位です。
電気の世界には電位というものが存在します。電位とは電気の世界で言う「高さ」のことだと考えて下さい。(正確には、ある点から基準点まで単位電荷(+1C)を動かした場合の外力(=静電気力)に逆らう仕事量のこと。)
物体が高いところから低いところに向かって落下するのと同じように、正の電荷も電位が高いところから低いところへ向かって移動します。(正確には、自由電子が電位の低いところから高いところへ移動しており、仮想的に等価な+電荷が電位の高いところから低いところに移動していると捉えます。)
この時の電荷の動きを電流と呼びます。
電流の単位はA[アンペア]であり、「毎秒1クーロンの電荷を流すような電流を1A」として定義されます。
電圧とは二点間の電位の差のことです。(厳密にはこの表現には少し問題がありますが、電位差のことと思ってもらって差し支えないです。)
電圧の単位はV[ボルト]であり、「1Aの電流が流れる導体の2点間において消費される電力が1Wであるとき、その2点間の電圧を1V」として定義されます。
電気抵抗とは字の表す通り、電流の流れやすさ(流れにくさ)のことです。
単位はΩ[オーム]であり、「1Vの電圧をかけたときに1Aの電流が流れる電気抵抗を1Ω」として定義されます。
電流が流れやすい物体、すなわち電気抵抗が小さい物体のことをを導体と言います。銅などが代表的な導体です。逆に電気抵抗が大きく電流をほとんど流さないような物体を絶縁体と言います。
物体によって電気抵抗が異なる理由について詳しく知りたい方はこちらの動画をご覧下さい。
https://youtu.be/viw4Fik2904
このように、中学校や高校で習った電気の話を利用して作られたものが電気回路です。
コンピュータは大変複雑な電気回路ではありますが、その動作の根幹にあるのは電気の働きです。
多くの技術者にとってはこのような知識は必要ないと思いますが、知っておくとコンピュータに対して少し親しみが湧きますね。
電気の話の次は、コンピュータで数を扱う方法について考えてみます。
2進数の話
コンピュータとは論理演算を実現した電子回路(=論理回路)です。
論理演算とは、ざっくり言えば「真」(命題が正しい)と「偽」(命題が正しくない)の2つの値だけを用いて行う演算のことです。
論理演算における「真, 偽」を「電圧の大, 小」や「電流の大, 小」、「メモリに電荷が蓄えられている, いない」などの電気的な2値で区別できる形に対応させることで、論理演算を電子回路で扱うことができます。
真偽の区別は多くの場合電圧の高低で区別します。
真を高電圧に対応させ、 偽を低電圧に対応させる方法が多く見られます。このような対応を正論理と言います。(もちろん真を低電圧に対応させ、偽を高電圧に対応させても理屈的には問題ありません。)
具体的な電圧の高低の値は、例えば5V電源だけを使う回路なら、高電圧は5V, 低電圧は0Vとなります。昔の半導体論理回路では5V電源のものが多かったようですが、最近はもっと低電圧で動くものが多くなっているらしいです。電圧が低い方が電力消費を抑えられるので経済的だからです。
また、コンピュータの計算には2進数(0と1だけを用いた計算)が採用されています。
論理演算における「真, 偽」を数字の「1, 0」に対応させることで、論理演算と数値演算を統一的に扱えます。
今までの話を整理すると、
論理演算の真/偽 = 数字の1/0 = 電圧の高/低
という対応関係になります。
コンピュータを動かしている命令の実体は、電圧の高/低などの2値の組み合わせで表現できる電気信号です。
それを分かりやすく1と0を使った2進数で書き表すというわけです。
このように情報を2値で扱うことのメリットについても考えてみます。
例えば、電圧の高低だけをコンピュータ内部で判定することで、ノイズが入りにくく、作りが簡単になるというメリットが挙げられます。
もし仮に、コンピュータに10段階の電圧の違いを判定させようとすれば、電圧が最も低い状態を0、それより少しだけ電圧が高い状態を1、更にそれより少しだけ電圧が高い状態を2, ... のような僅かな違いを正しく判定せねばならず、その分作りが複雑になるでしょう。複雑になればなるほど判定を誤って情報の伝達ミスが起こる可能性も高まります。
電圧が高いか、低いかという2元的な情報だけを判断するのであれば判断ミスは起こりにくいですし、作りも簡単になります。
もしノイズやその他の問題を解決できるのであれば、2値だけと言わず、3値, 4値...とより多くの情報を1つのトランジスタで扱えるようにすることで、コンピュータを高性能化できる可能性があります。
そのため多値論理をコンピュータに導入する研究も盛んに行われているようです。(https://engineer.fabcross.jp/archeive/190614_shrinking-transistors.html )
論理代数
x が論理値(真理値)をもつとは、xが0(偽)か1(真)のどちらかの値を取ることを言います。
すなわち
x ≠ 0 ならば x = 1
x ≠ 1 ならば x = 0
が成り立つことを言います。
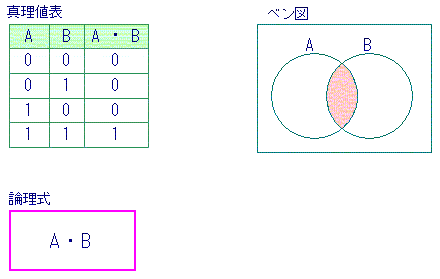
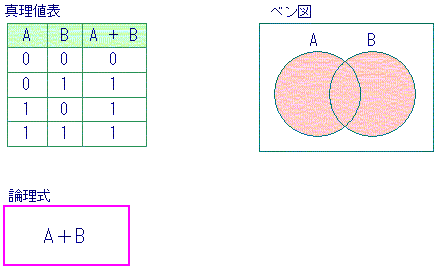
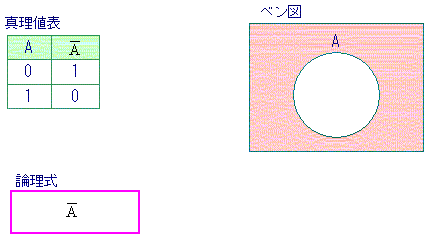
論理代数は、論理値 (0,1) に関する、論理積(AND)、論理和(OR)、否定(NOT)という三つの演算からなる代数系として定義されます。なお、論理積、論理和、否定は次のように定義されます。
論理関数の全ての入力の組合せに対する出力を列挙した表を真理値表と呼びます。当然ですが真理値表と論理関数は1対1に対応します。すなわち、一つの真理値表はただ一つの論理関数に対応し、一つの論理関数はただ一つの真理値表により表現されるということです。
一方、論理式は論理関数の一意な表現ではありません。一つの論理式はただ一つの論理関数を定めますが、一つの論理関数は複数の(無数の)論理式で表現できます。
任意の論理関数に対して,それを表す論理式が少なくとも一つは存在することを、論理式の完全性と言います。
では、論理式で(AND,OR,NOTを使って)全ての論理関数が表現できることを示します。
シャノン展開
任意の論理関数 F(x1, x2, x3, . . . , xn) は,以下のとおり展開できる.
F(x1,x2,x3,...,xn)
= x1 ̄·F(0,x2,x3,...,xn) + x1·F(1,x2,x3,...,xn)
これが成り立つことは、x1が0の場合と1の場合でそれぞれ両辺を比較すれば明らかでしょう。
シャノン展開によりn変数論理関数を2つの(n-1)変数論理関数の和(OR)の形に展開できます。得られた2つの論理関数それぞれについてもシャノン展開を行うという操作を繰り返せば、最終的に0または1の定数関数だけからなる展開式となります。
以上により、AND、OR、NOTの3つの演算の組み合わせであらゆる論理関数を記述できることが示されました。
例として任意の3変数論理関数 F(x, y, z) を論理式で表現してみます。
F(x, y, z)
= x ̄・F(0, y, z) + x・F(1, y, z)
= x ̄・(y ̄・F(0,0,z) + y・F(0,1,z))
+ x・(y ̄・F(1,0,z) + y・F(1,1,z))
= x ̄・(y ̄・(z ̄・F(0, 0, 0) + z・F・(0, 0, 1))
+ y・(z ̄・F(0, 1, 0) + z・F(0, 1, 1)))
+
x・(y ̄・(z ̄・F(1, 0, 0) + z・F(1, 0, 1))
+ y・(z ̄・F(1, 1, 0) + z・F(1, 1, 1)))
= x ̄・y ̄・z ̄・F(0, 0, 0)
+ x ̄・y ̄・z・F(0, 0, 1)
+ x ̄・y・z ̄・F(0, 1, 0)
+ x ̄・y・z・F(0, 1, 1)
+ x・y ̄・z ̄・F(1, 0, 0)
+ x・y ̄・z・F(1, 0, 1)
+ x・y・z ̄・F(1, 1, 0)
+ x・y・z・F(1, 1, 1)
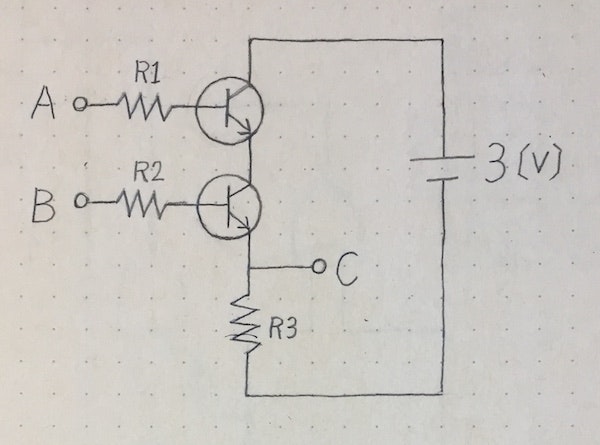
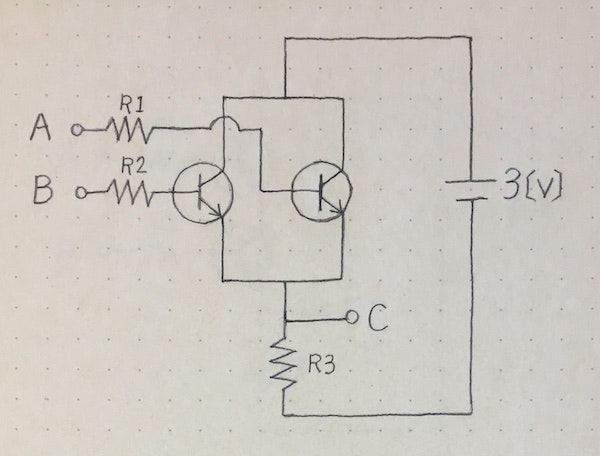
上記のAND, OR,NOTの演算は電気回路で実現することが可能で、例えば次のようになります。
(画像はhttps://sagara-works.jp/ より引用。こちらのサイトも大変勉強になりました。)
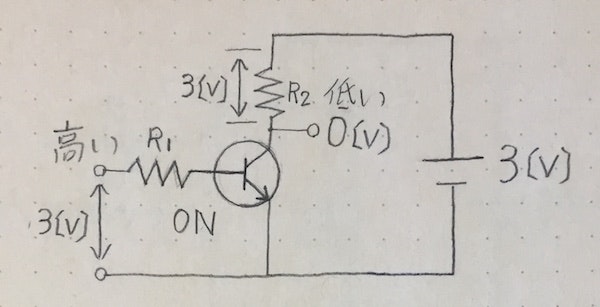
実際の電気回路ではないですが、回路を次のように簡易的に表現したものを論理ゲートと言います。
(画像はhttps://youtu.be/-EkN6ulxw54 より引用。)
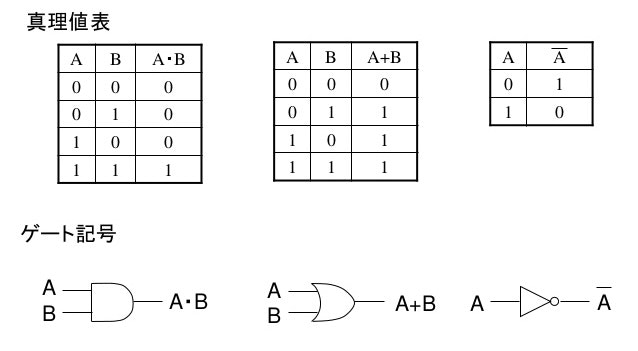
AND、OR、NOTの3つの演算であらゆる論理式を記述可能であり、また、これらの演算は電気回路で表せるので、電気回路で様々な論理演算を実現することが可能であることが分かります。
ここからはコンピュータの動きをより具体的にイメージするために、機械語とデコーダについて簡単にご紹介します。
機械語
CPUには、そのCPUで実行可能な命令のセットがあらかじめ準備してあり、それらを組み合わせてプログラムを作ります。
しかし、数字の羅列である機械語命令を直接扱うのは困難なので、プログラミングしやすくするための簡略記憶記号としてニーモニックという表記が使われます。
ニーモニックは、機械語命令の機能一つ一つに名前を付けて人間に分かりやすいかたちで表現したものです。(例えば加算を表す命令なら「ADD」など。)
例を見た方がイメージが掴みやすいと思うので、次を見て下さい。
16bitで表される命令のうち、上5桁(赤字の部分)が命令の種類となっています。
例 : 1+2+3+…+10を計算する.
命令0
(機械語)
0100100000000000
(ニーモニック)
ldh(REG0, 0)
(意味)
レジスタ000(16bitの情報を保存できる記憶素子)の上8桁に00000000を書き込む
命令1
(機械語)
0100000000000000
(ニーモニック)
ldl(REG0, 0)
(意味)
レジスタ000の下8桁に00000000を書き込む
命令2
(機械語)
0100100100000000
(ニーモニック)
ldh(REG1, 0)
(意味)
レジスタ001の上8桁に00000000を書き込む
命令3
(機械語)
0100000100000001
(ニーモニック)
ldl(REG1, 1)
(意味)
レジスタ001の下8桁に00000001を書き込む
命令4
(機械語)
0100101000000000
(ニーモニック)
ldh(REG2, 0)
(意味)
レジスタ010の上8桁に00000000を書き込む
命令5
(機械語)
0100001000000000
(ニーモニック)
ldl(REG2, 0)
(意味)
レジスタ010の下8桁に00000000を書き込む
命令6
(機械語)
0100101100000000
(ニーモニック)
ldh(REG3, 0)
(意味)
レジスタ011の上8桁に00000000を書き込む
命令7
(機械語)
0100001100001010
(ニーモニック)
ldl(REG3, 10)
(意味)
レジスタ011の下8桁に00001010を書き込む
命令8
(機械語)
00001010001----
(注 : -は命令に関係のない部分で0と1どちらでもよい)
(ニーモニック)
add(REG2, REG1)
(意味)
レジスタ001の値をレジスタ010に加算する
命令9
(機械語)
00001000010-----
(ニーモニック)
add(REG0, REG2)
(意味)
レジスタ010の値をレジスタ000に加算する
命令10
(機械語)
0111000001000000
(ニーモニック)
st(REG0, 64)
(意味)
RAM(I/O)の01000000番地にREG000の値を出力する
命令11
(機械語)
01010010011-----
(ニーモニック)
cmp(REG2, REG3)
(意味)
REG010とREG011を比較して一致すれば Flag = 1 とする
命令12
(機械語)
01011---00001110
(ニーモニック)
je(14)
(意味)
Flag = 1 であれば00001110(命令14)に飛ぶ
命令13
(機械語)
01100---00001000
(ニーモニック)
jmp(8)
(意味)
00001000(命令8)に無条件で飛ぶ
命令14
(機械語)
01111-----------
(ニーモニック)
hlt()
(意味)
CPUを停止する
簡単にプログラム全体の説明をします。
REG1は定数(=1)です。
REG3も定数(=10)です。
REG2は初期値が1で、1回ループするごとにREG1の値(=1)が加算されます。従ってREG2の値はループ回数を表します。
REG0は初期値が0で、1回ループするごとにREG2の値、即ちループ回数が加算されます。
よってREG0 = 0 + 1 + 2 … と値が増加していきます。
REG2 = REG3となったら(即ち10回ループ後)命令14に飛んで計算を終了します。
終了前の最後のループでは、
REG0 = 0 + 1 + 2 + … + 10 = 55 となっています。
こちらの例と命令コードは動かしてわかるCPUの作り方10講にあるものと同じものを使わせていただきました。(もちろん、命令コード自体に意味があるわけではないので、何らかの命令に対して好きな2進数を割り振って構いません。)
この本も購入して読みましたが、大変参考になりました。初めてコンピュータアーキテクチャを学ぶ人にも読みやすく、それでいて内容もしっかりしている本だと思うので、興味のある人は是非読んでみて下さい。
デコーダ
エンコーダ(符号器)とは人間が扱う10進数や文字などの情報を、コンピュータが扱う2進数やコード情報に変換するための回路です。
一方、デコーダ(復号器)とはその逆に、演算結果の2進数を10進数に変換して液晶に表示したりする回路です。
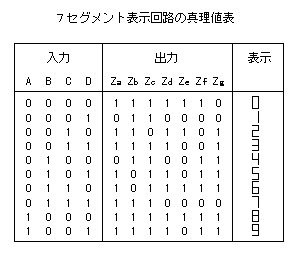
有名や例として4桁の2進数を10進数(0〜9)として表示するデコーダ回路を見てみましょう。
これは7セグメントLEDディスプレイと呼ばれます。
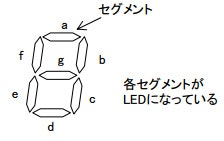
例えば「3」を表示したければa,b,c,d,gを1(点灯)にします。
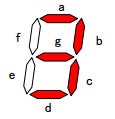
直感的に理解しやすい例なので、特に説明がなくとも2進数を10進数として表示できていることが分かると思います。「7セグメントLED」などのワードで検索すれば色々と出てきます。
最後に
素人なりに勉強して書きましたが、間違った記述があれば訂正するので教えて下さい。
長くなりましたが、最後まで読んで下さってありがとうございました。