はじめに
最近、大学時代の友人と趣味で集合論を学び直しました。 内田伏一先生の「集合と位相」(旧版)を、行間を全て埋める形で読み進めました。 せっかくなので記憶が新しいうちに学習内容を記事にして共有します。 全内容を網羅するわけでなく、初学者(数学を専攻したことがないエンジニア)向けに要点だけをかいつまんで書いていくので、興味があれば読んでみてください。 また、僕の思い付きで始めた勉強会に快く付き合ってくれた、京都大学大学院理学研究科・山崎君に感謝します。エンジニアが集合論を学ぶ意義
集合論は確率論の基礎となり、確率論は統計学の基礎となっています。 そのため、データサイエンス系の道に進むことを考えている方にとって、統計学の学習の前段階として、集合論の基礎を知ることは重要かと思います。集合とは
「ある条件を満たすものの集まり」を集合と言います。 集合を構成する一つ一つのものを元または要素と言います。 aが集合Aの元であるとき、aはAに含まれると言い、a∈Aと書きます。集合の表記法
例として、「1以上5以下の整数」という集合Aを考えます。 集合Aの表記法としては、主に次の二つがあります。① {1, 2, 3, 4, 5}
② {x∈$\mathbb{N}$|1≦x≦5}
①のように単純に元を書き並べてもよいですが、②のように
{x|xの満たす条件}
という形式で書くことも多いです。
部分集合
二つの集合A,Bについて、「Aのどの元もBに含まれる」とき、AはBの部分集合であると言い、A⊂Bと書きます。 またこのとき、AはBに包まれると言います。(参考)
A⊂Bであることを、AはBに含まれると表現することも多いですが、元と集合との関係(a∈A)と、集合どうしの関係(A⊂B)とを区別するために、前者を「含まれる」、後者を「包まれる」と呼び分けることを個人的にはオススメします。
集合どうしが等しいことの証明
二つの集合A,BがA=Bであること(集合として等しいこと)を示したい場合、 A⊂B かつ A⊃B であることを示します。 すなわち、 ①Aのどの元もBに含まれること(∀a∈A ⇒ a∈B) ②Bのどの元もAに含まれること(∀b∈B ⇒ b∈A) を示します。(注)
∀は「任意の」を表す記号です。「任意の」というのは、特別な選び方をしないという意味です。任意のa∈Aについて条件Pが成り立つということは、(特別な選び方をせずに)どのように元を選んだとしても条件Pが成り立つということ、すなわち、全てのAの元に対して条件Pが成り立つということです。
集合族
時々躓く人がいる概念がこの集合族です。 集合族とは、「集合の集合」のことです。 集合とは単一の元だけを集めてできるものを指すとは限りません。 集合を集めてできるものもまた集合です。 集合を集めてできる集合(全ての元が集合であるような集合)を強調して集合族と呼びます。(例)
A,B,Cを集合とするとき、それらを元とする集合{A, B, C}は集合族
和集合と共通部分
「Aの元とBの元とを全て合わせてできる集合」を、AとBの和集合と言い、A∪Bと書きます。 すなわち、 A∪B = {x|x∈A または x∈B} です。 また、「AとBの両方に含まれる元を全て集めてできる集合」を、AとBの共通部分と言い、A∩Bと書きます。 すなわち、 A∩B = {x|x∈A かつ x∈B} です。なお、和集合と共通部分については、交換法則・結合法則・分配法則が全て成り立ちます。
・A∪B = B∪A
・A∩B = B∩A
・(A∪B)∪C = A∪(B∪C)
・(A∩B)∩C = A∩(B∩C)
・A∪(B∩C) = (A∪B)∩(A∪C)
・A∩(B∪C) = (A∩B)∪(A∩C)
式変形する時、扱いやすくて助かりますね。
この性質も重要なので押さえておきたいです。
直積
二つのの集合A,Bに対して、「a∈A かつ b∈B であるような全てのaとbの組(a,b)の集合」をAとBの直積と言い、A×Bと書きます。 エンジニアの方には、SQLのCROSS JOINと言った方が馴染みがあるかもしれません。(例)
A = {a, b, c}, B = {1, 2}のとき、
A×B = {(a,1), (a,2), (b,1), (b,2), (c,1), (c,2)}
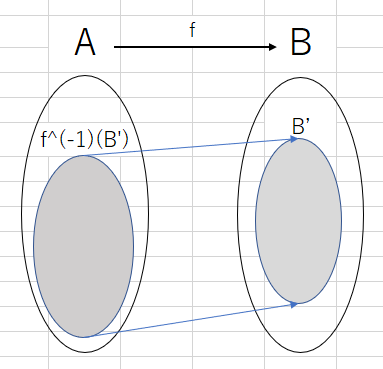
写像とは
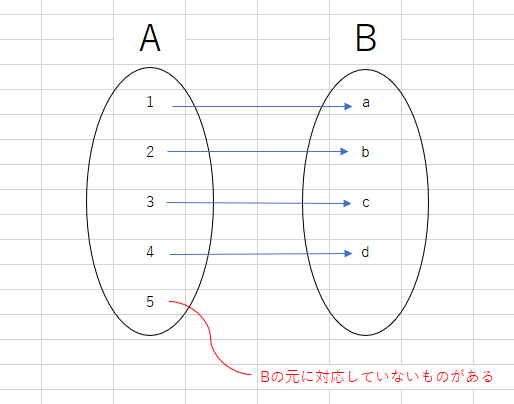
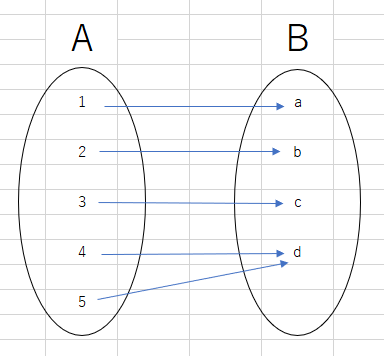
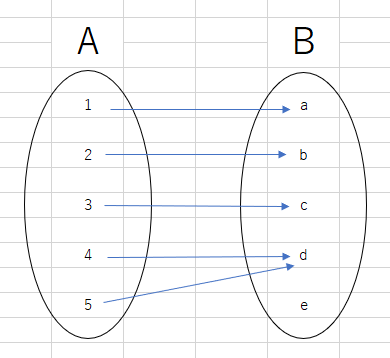
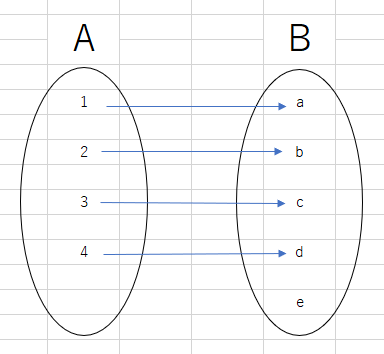
写像をしっかり理解して使いこなせるかが集合論では肝要です。 「集合Aの全ての元に対して集合Bの元を一つ対応させる規則f」のことを、AからBへの写像と言い、f:A→Bと書きます。 また、Aをfの始域、Bをfの終域と言います。 写像とは簡単に言えば集合と集合との対応関係のことですが、注意してほしいのが、集合と集合との対応関係ならば何でも写像と呼んでよいわけではないということです。 写像とは、Aの「全ての」元を、Bの元に「一つ」対応させる規則のことですから、例えば次のようにAの元をBの元に対応させきっていないものは写像とは言いません。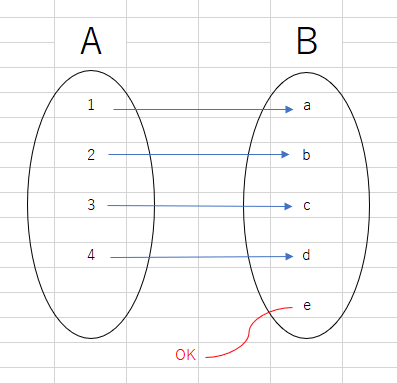
また、Aの元がBの二つの元に対応してしまっているようなものも(AからBへの)写像とは言いません。
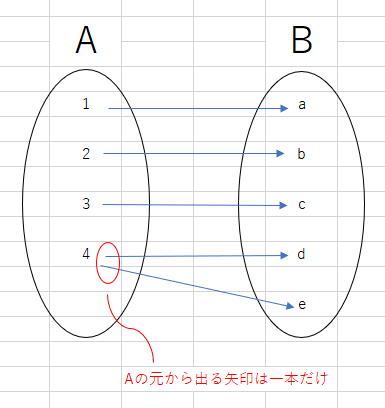
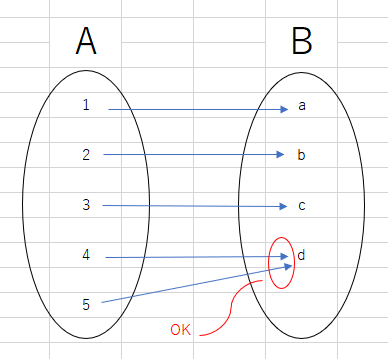
ただし、Aの別々の元がBの同じ元に対応しているようなものはOKです。
・始域の元は全て終域に飛ばす
・始域の一つの元から出る矢印は一本
ということを忘れないようにして下さい。
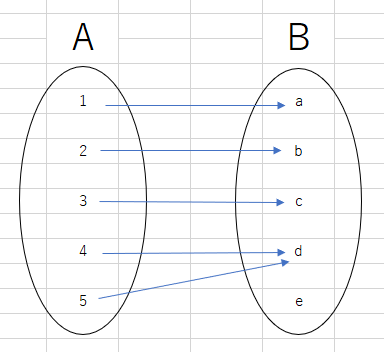
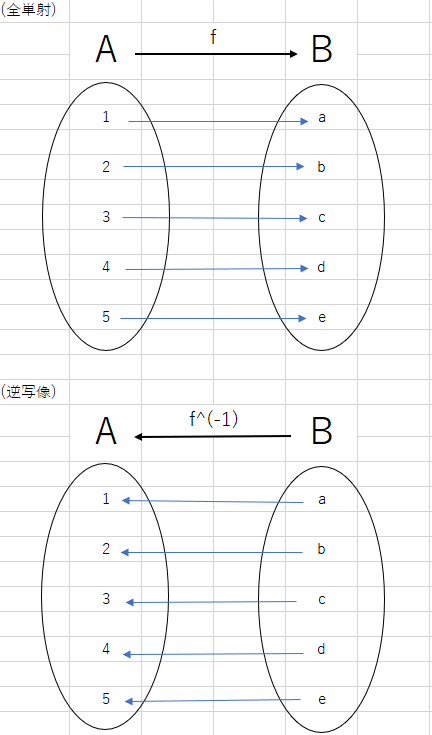
全射・単射
写像の中でも特に、「終域の全ての元に矢印が伸びているようなもの」を全射と言います。(終域の元を全て射つ)写像の中でも特に、「終域の一つの元に対して二本以上矢印が伸びていないもの」を単射と言います。(終域の元を単(ひと)つ射つ)
イメージとしては上記で問題ないですが、数学ですからもう少しキチンと定義しておく必要があります。
ここまでの図によるイメージが掴めていれば、正確な定義もスッと理解できると思います。
fは全射である
⇔f:A→Bについて, Bのどんな元bに対してもb=f(a)となるAの元aが常に存在する
fは単射である
⇔Aの元a_1, a_2に対して、f(a_1)=f(a_2)ならば常にa_1=a_2である
また、写像fが全射かつ単射であるとき、fは全単射であると言います。
(参考)
単射の定義は、
Aの元a_1, a_2に対して、a_1≠a_2ならば常にf(a_1)≠f(a_2)である
としてもよい(対偶をとっただけなので同じこと)ですが、f(a_1)=f(a_2)⇒a_1=a_2の方が使い勝手がよいので、こちらを覚えておくのがよいかと思います。