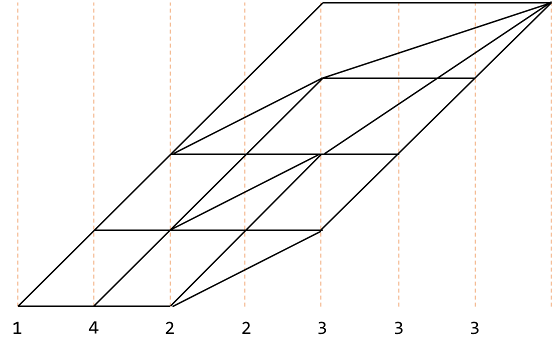面白そうな問題を見つけたので解いてみました。
問題
$N$枚のカードがあり、$i$番目のカードには$A_i$が書かれている。
T君はこの中から$M$枚を同時に抜き出す。取り出されたカードに書かれた数字のペアは何通りあるか。
ただし、$(1,2)$と$(2,1)$のような順序を入れ替えただけのペアは区別しない。
例えば$N=5$, $M=2$, $\{A\}=\{1,2,2,3,4\}$の場合を考えてみましょう。この場合は$(1,2),(1,3),(1,4),(2,2),(2,3),(2,4),(3,4)$の$7$通りのペアがあります。
もう数え上げも怖くない ~競プロ数え上げ問題35選~ - Qiita の問題を一部改変しました。
この記事を書いている人
この記事を書いている人は競技プログラミング未経験です。
競プロのお作法などはよく分かっていないので、そのへんは大目にみてください。
前提知識
格子経路の数
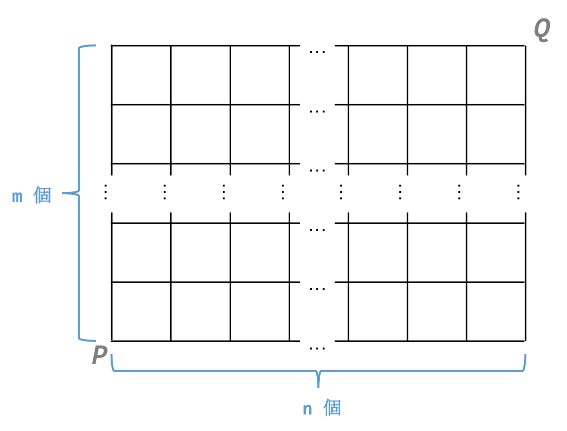
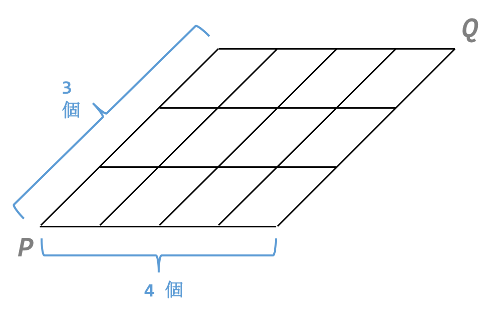
このような格子状の経路を考えます。
右か上にしか進めない場合、$P$から$Q$までの経路数は
{}_{n+m} \mathrm{C} _m
です。
経路数を1ステップごとに計算する
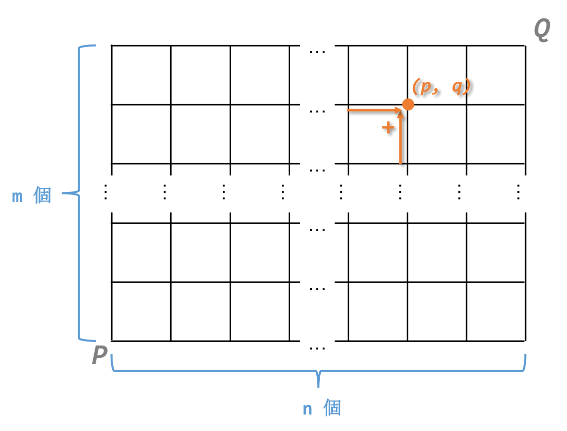
前出の格子経路の数の問題で、横軸を$p$,縦軸を$q$として、ある点$(p, q)$への経路数は、$(p-1, q)$と$(p, q-1)$への経路数を足したものです。
この性質を利用して、$P$からの距離1を$1$ずつ増やしながら計算します。最後まで進むと、求める値が得られます。
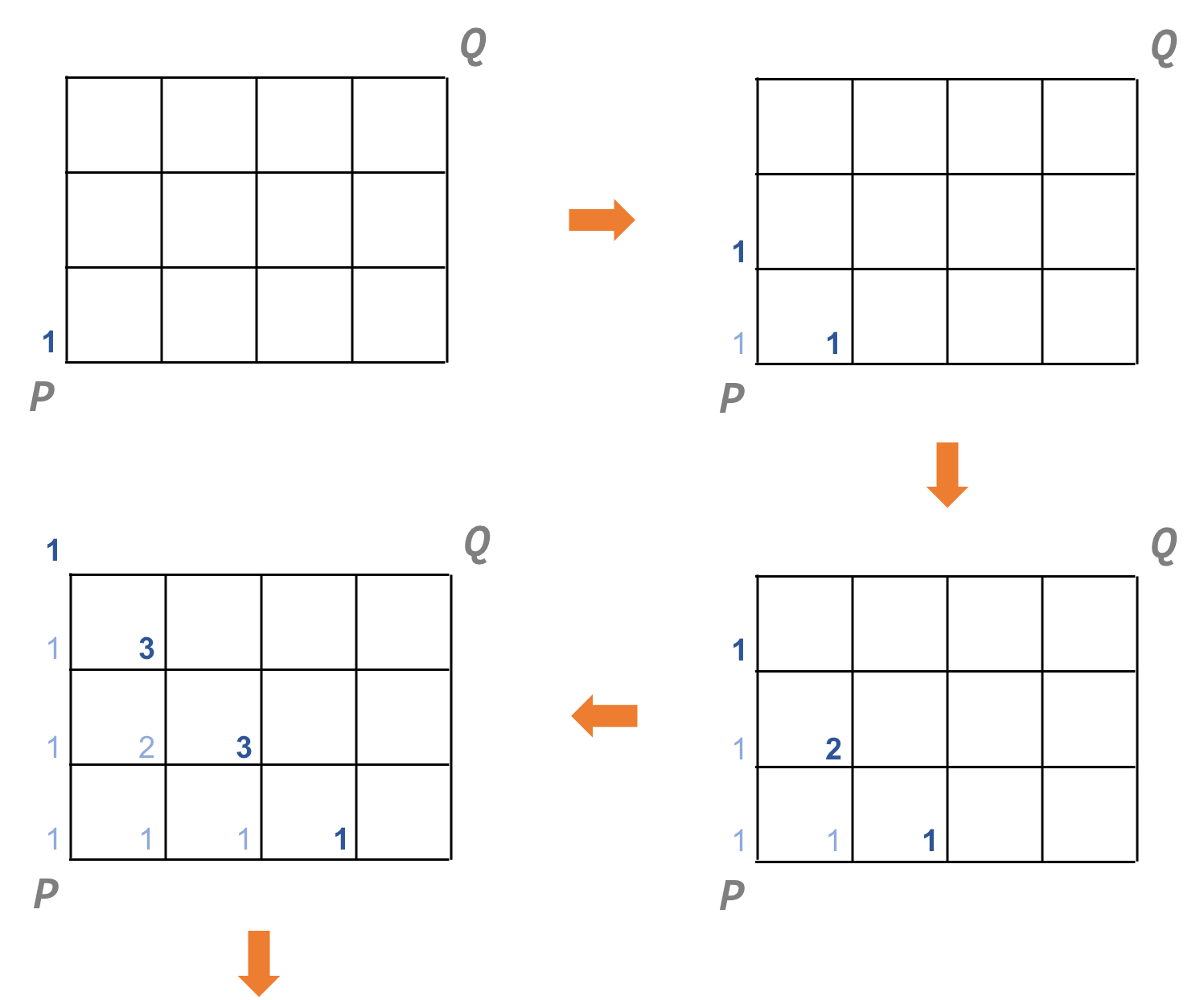
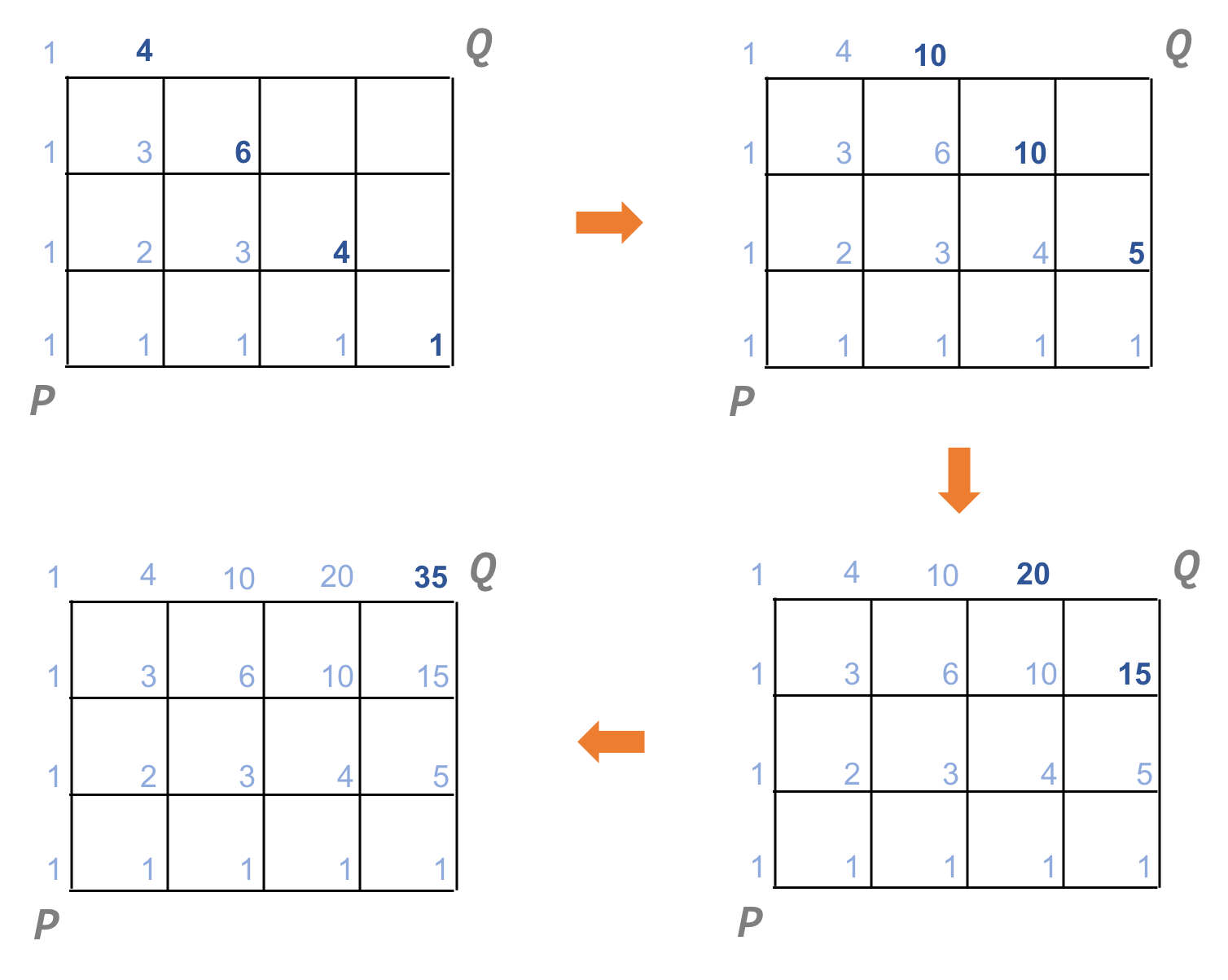
$ 4 \times 3 $ の格子で確かめてみましょう。
$4 \times 3$ の格子の経路数は35であることが分かりました。この結果は ${}_7 \mathrm{C} _3=35$ と一致します。
格子の変形
以降の節でこのような格子が出てきます。縦軸が斜めになっただけで、組み合わせの数は変わりません。
本題のアルゴリズム
$N$枚のカードがあり、$i$番目のカードには$A_i$が書かれている。
T君はこの中から$M$枚を同時に抜き出す。取り出されたカードに書かれた数字のペアは何通りあるか。
ただし、$(1,2)$と$(2,1)$のような順序を入れ替えただけのペアは区別しない。
$N=7$, $M=4$, $\{A\}=\{1,2,2,3,3,3,4\}$の場合を考えてみましょう。
格子の作成
まず、以下のような格子を作成します。
格子の横軸には$A$に含まれる数字を書きます。同じ数字が含まれている場合は連続して書きます。
黒い実線は下に書かれた数字を使うかどうかを表します。右上に進む場合はその数字を使用することを意味し、右横に進む場合はその数字を使わないことを表します。
例えば、
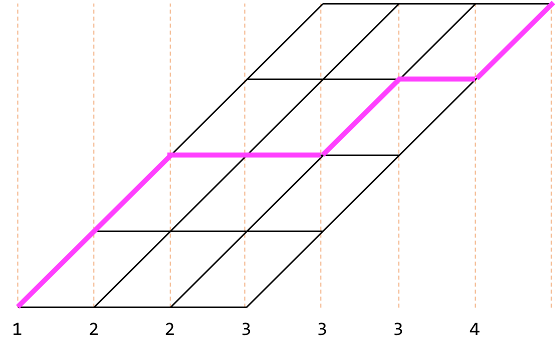
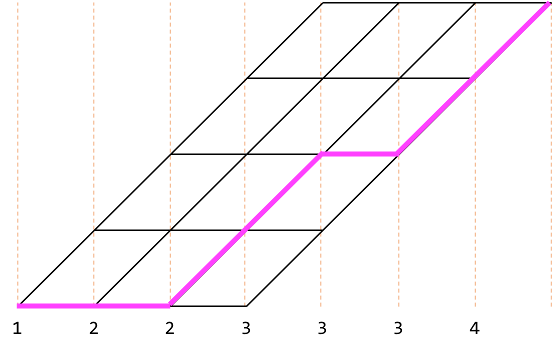
ピンク色で表された経路は $(1, 2, 3, 4)$ を選択することを表します。
同様に、
は $( 2, 2, 3, 3)$ を選択することを表します。
重複した組み合わせ
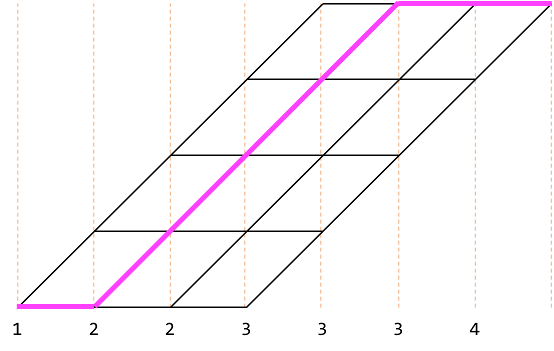
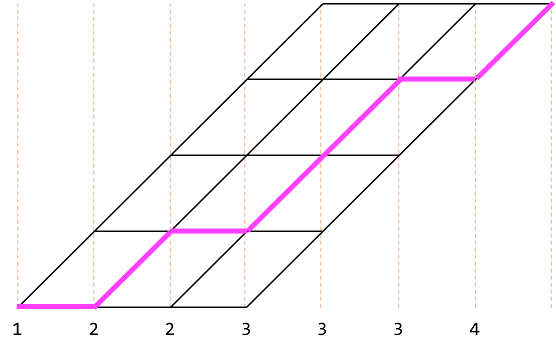
この方法では、
と
は両方とも$(2, 3 ,3, 4)$を選択することを表しており、1つの組み合わせに対して経路が複数あります。
重複した組み合わせを避ける
1つの組み合わせに対して、1つの経路になるように経路を変更します。
数字を選択する際、同じ数字がある場合は、選択した数字の右にある同じ数字全てを選択するという経路に変更します。これによって重複する組み合わせを排除することができます。
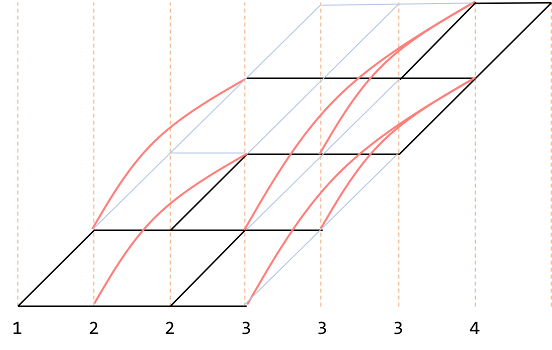
薄い青線が削除した経路、赤が追加した経路です。左側の$2$を選択した場合、右側の$2$も選択します。同様に一番左の$3$を選択した場合には残り2つの$3$も選択し、真ん中の$3$を選択した場合には右の$3$も選択します。
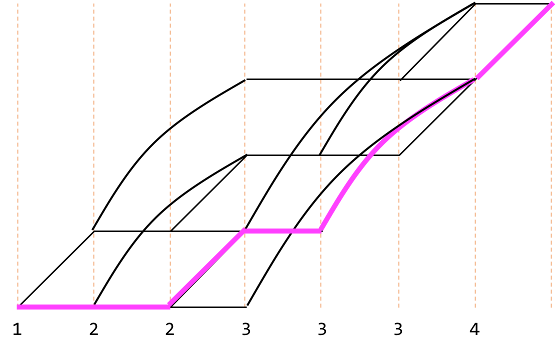
これによって、$(2, 3 ,3, 4)$を選択する経路は以下の経路のみになりました。
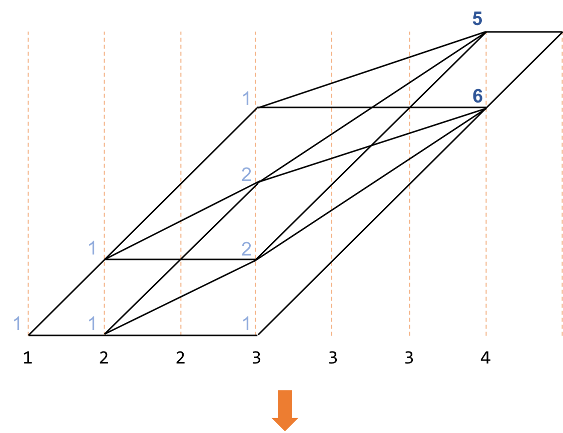
数え上げ
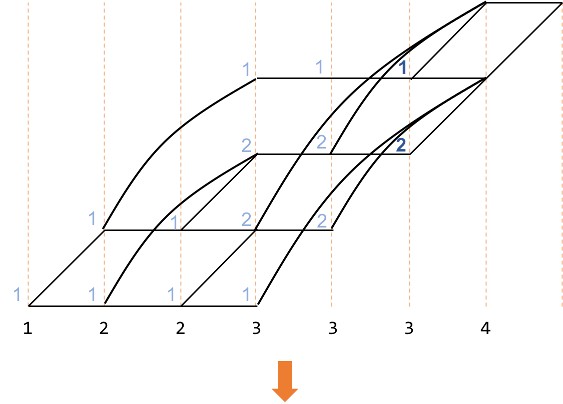
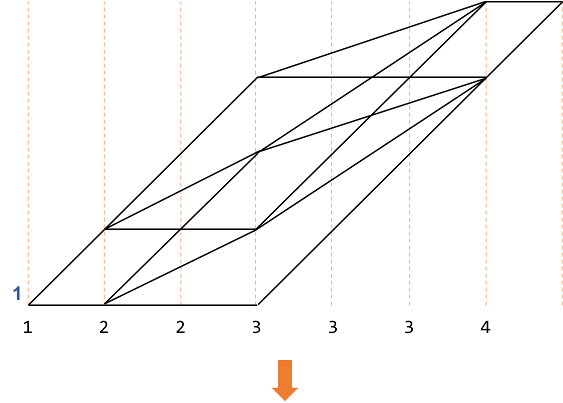
作成した経路で数え上げをします。
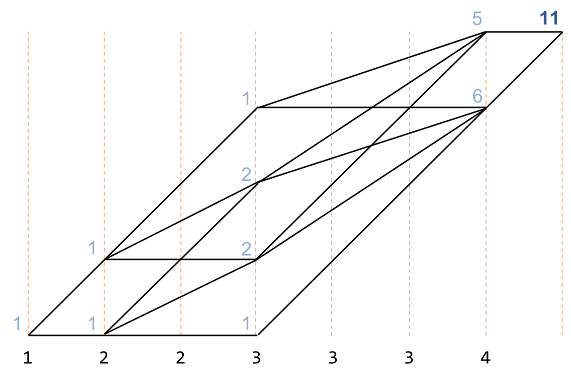
この操作によって、 $\{A\}=\{1,2,2,3,3,3,4\}$から4つを選ぶ場合の数は$11$であることがわかりました。
重複する数字の選択方法
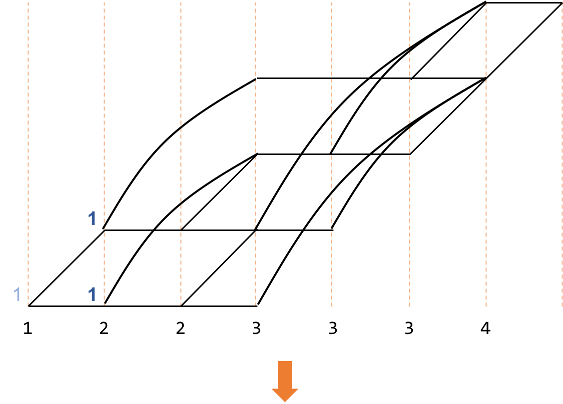
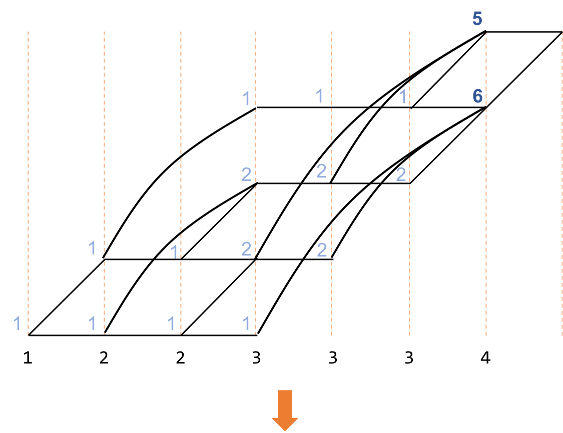
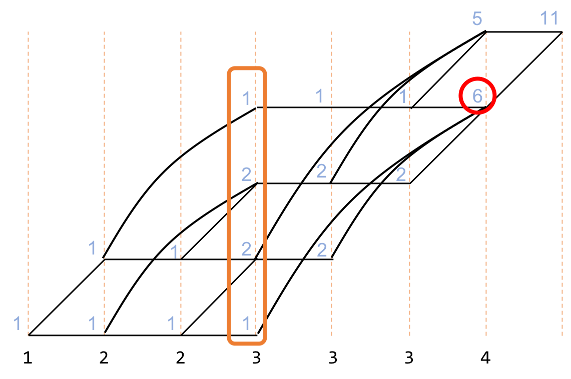
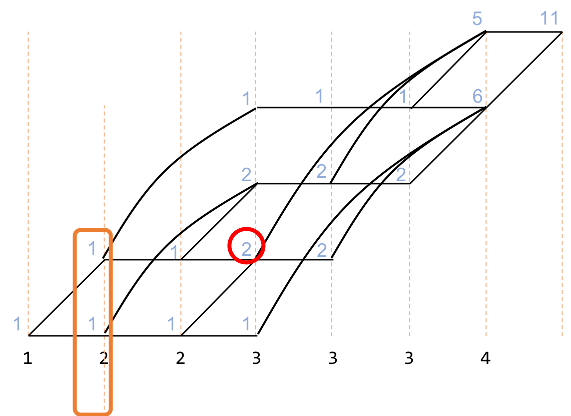
ここで、赤で示した部分に注目します。
この数字は、オレンジで囲んだ部分を足したものです。
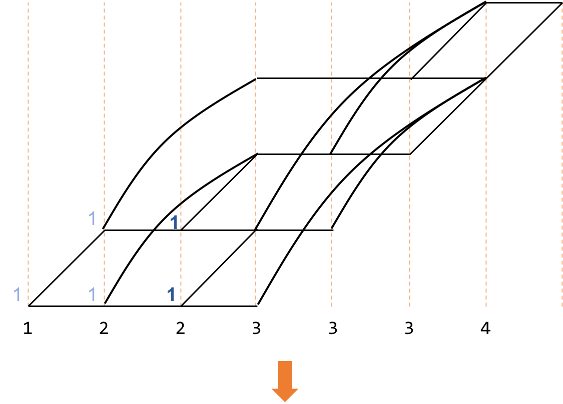
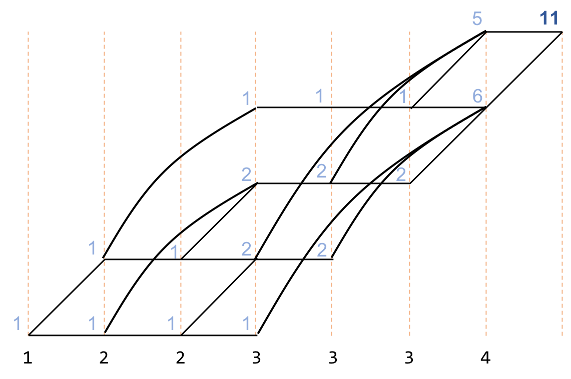
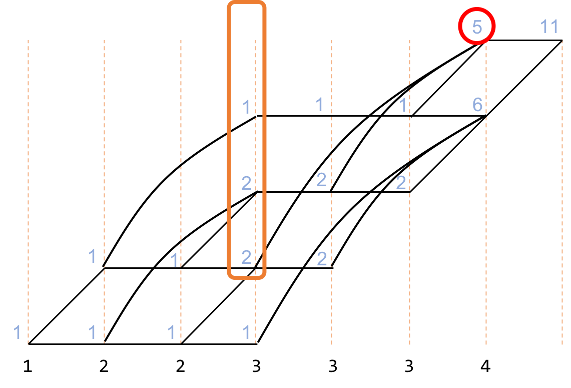
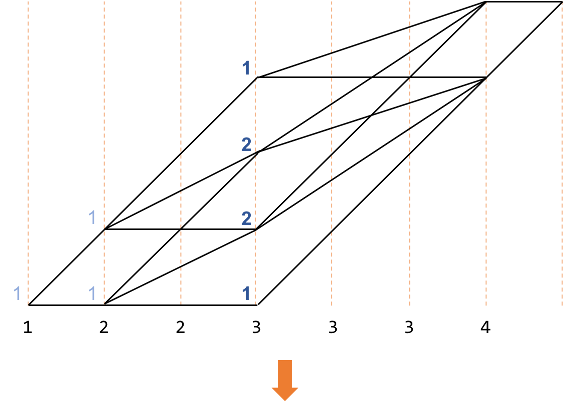
同様に以下の図で赤で示した部分は、オレンジで囲んだ部分を足したものです。
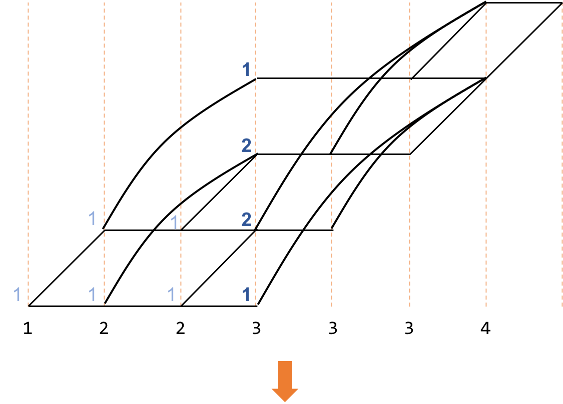
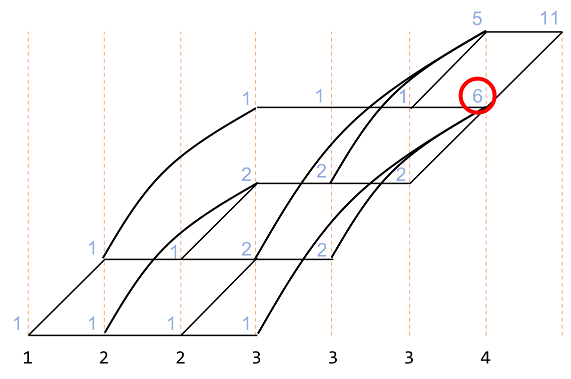
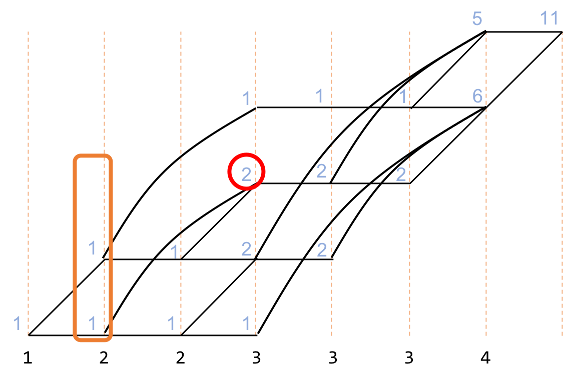
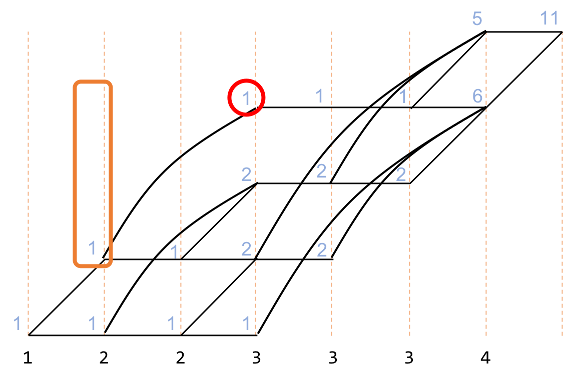
同様に以下の図で赤で示した部分は、オレンジで囲んだ部分を足したものです。
通常の格子では、点$(p, q)$への経路数は、$(p-1, q)$への経路数と$(p, q-1)$の経路数を足したものでした。
同様に同じ数字が2つある場合、$(p, q)$への経路数は、$(p-2, q)$, $(p-1, q-1)$, $(p, q-2)$ それぞれの経路数を足したものです。
同様に同じ数字が3つある場合、$(p, q)$への経路数は、$(p-3, q)$, $(p-2, q-1)$, $(p-1, p-2)$, $(p, q-3)$ それぞれの経路数を足したものです。
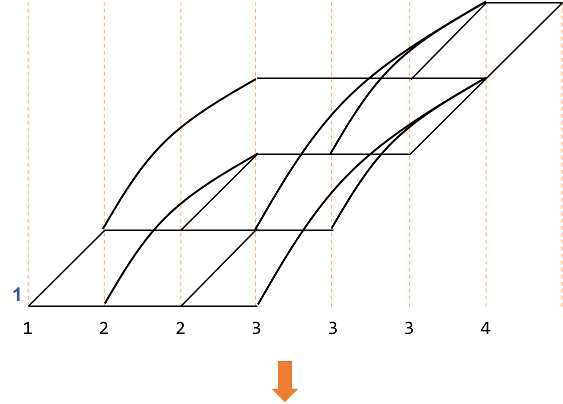
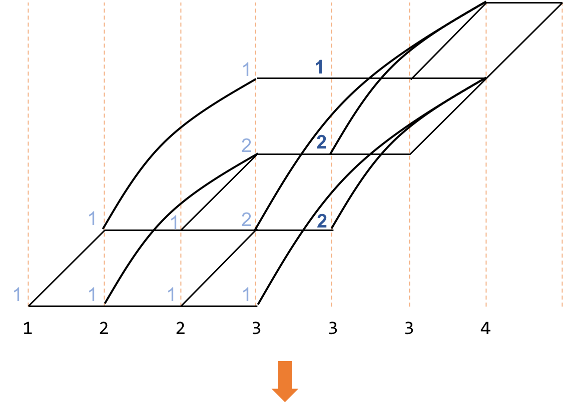
経路図は、以下のように書き換えることができることが分かります。
数え上げ(再び)
書き換えた経路で再び数え上げをします。
ここまでで、重複した数字を含む$N$枚のカードから$M$枚を選ぶアルゴリズムの具体例を確認できました。
アルゴリズム
上記アルゴリズムを一般化します。
- $A$はカードの集合を表す
- $点(p, q)$への経路数を$route(p, q)$で表す。$route(0, 0) = 1$である
- 原点からの距離を$step$で表す。stepの初期値は$0$である
- $A$が空になるまで以下を繰り返す
2. $A$から1種類の数字$a$を全て取り出し、$A$からは削除する。$a$がいくつあるかを$c$とする
3. $step$に$c$を加える
4. $p + q = step\ (0 \leqq p \leqq N-M, 0 \leqq q \leqq M)$ を満たす整数$(p, q)$について、
$route(p, q) = route(p - c, q) + route(p - c + 1, q -1) + route(p - c + 2, q - 2) + ... + route(p - 1, q- (c -1)) + route(p, q - c)$ を計算する - $route(N-M, M)$ が求める数である。
アルゴリズムの修正
上記アルゴリズムは、$N=7$, $M=2$, $\{A\}=\{1,2,2,3,3,3,4\}$ など、$M$より大きな重複度をもつ数字があるとうまくいきません(今回は$3$が3つある)。$M$個以上重複する数字がある場合は、事前に重複度を$M$に減らしておく必要があります。
アルゴリズムの改善
数字の重複度ごとに並べる
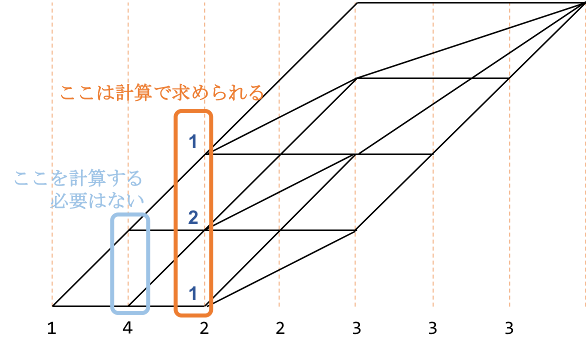
数字を重複度ごとに並べましょう。1回しか現れない数字を一番左側に書きます。
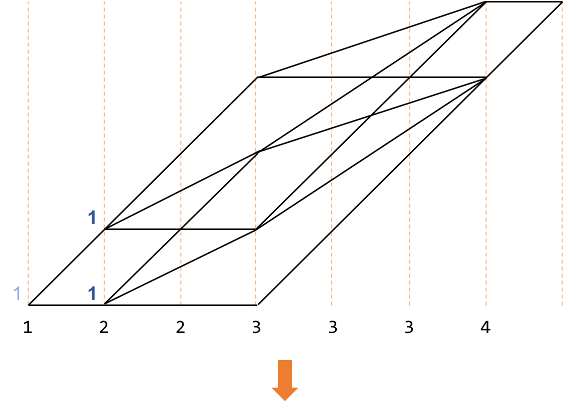
1回しか現れない場合の数は計算で求めることができます。
(リンクしたプログラムで$step$が$0$から始まっていないのはこのためです。)
単純な格子の場合、対角線上には、$(x + y)^n$ を展開した時の係数が現れます(パスカルの3角形/二項定理)。
同様に同じ数字が2個現れる時にも規則性がありますが、まだうまく一般化できていません(私が)。2個現れる場合の数は、$(x^2 + x + 1)^n$の係数と関係があります。この性質を利用すればアルゴリズムをさらに改良することができます。
コード
上記アルゴリズムをPython(バージョン3.7)で実装しました。
combination.count_uniq_combination_lattice
プログラムが合っているかどうかはこちらの愚直解と同じかどうかで確認しています。
combination. count_uniq_combination_simple
参考リンク
あとがき
問題を初めて見たときは、「どこから手をつけていいか分からない。。」と思っていましたが、
解説記事を書いた今は、「あれ?これ意外とシンプルだし、競プロ界では常識なのかも」と思いはじめています。
もしかしたら既に同様の解説記事はあるのかもしれませんが、自身の整理用としてよかったので公開します。
-
ここでの距離は、格子の交差点から直近の交差点の長さを1としたもの ↩