もう数え上げも怖くない ~競プロ数え上げ問題35選~ - Qiitaの記事で紹介されていた問題のうち1つが面白そうだったので解いてみました。ちなみに問題を解きながら考えたことを含めて書いたため、最短で解にたどり着いていません。最短&最良の解を見たい場合は問題文のページから模範解答がリンクされていますのでそちらをご覧ください。
問題
$2N$ 個のマスが左右一列に並んでおり、各マスの色を表す長さ $2N$ の文字列 $S$ が与えられます。
左から $i$ 番目のマスの色は、 $S$ の $i$ 文字目が'B'のとき黒色で'W'のとき白色です。
あなたは異なる $2$ マスを選んで、それらのマスおよびそれらの間にあるマスの色を反転する操作をちょうど $N$ 回行います。 ここで、マスの色を反転するとは、そのマスの色が黒色なら白色に、白色なら黒色にすることです。
ただし、操作を通して同じマスを $2$ 回以上選ぶことはできません。 つまり、各マスがちょうど $1$ 回ずつ選ばれることになります。
$N$ 回の操作終了後に全てのマスを白色にする方法が何通りあるかを $10^9+7$ で割った余りを求めてください。
ここで、条件を満たす $2$ つの方法が異なるとは、$1$ つ目の方法で $i$ 番目に選んだ $2$ つのマスの組と
$2$ つ目の方法で $i$ 番目に選んだ $2$ つのマスの組が異なるような $i (1\leq i \leq N)$ が存在することをいいます。
ちょっとさわってみよう
Bを●または黒、Wを○または白で表します。'反転'には'ひっくり返す'という言葉を使っています。オセロをイメージしてください。
問題文に、●○●●○○○● の例が載っているので、これを解いてみましょう。
手始めに、手順にそってひっくり返してみましょう。
これは ○○○○○○○○ になりませんでした。
もう1回試してみましょう。
これは ○○○○○○○○ になりました。
ひっくり返す手順を、ひっくり返す順に位置をペアにして記載しましょう。
上記の例では、$(2,8)(1,4)(6,7)(3,5)$ になります。このような、ひっくり返す順のペアを並べたものを反転列と呼びましょう。
ひっくり返す順番は関係ない
いくつか試すと、ひっくり返すペアが同じであれば、ひっくり返す順番は最終的に出来上がるマスの模様に関係ないことがわかります。
例えば、$(2,8)(1,4)(6,7)(3,5)$ と $(1,4)(2,8)(3,5)(6,7)$ は同じ結果になります。
なお、以降マスの模様を白黒パターンと呼びます。
反転列を正規化する
反転列はペア同士を入れ替えても最終的に出来上がる模様(白黒パターン)は同じなので、規則を決めて一意に定まるようにします。この操作を反転列の正規化と呼びましょう。
- 小さい方の数字を左に書く
- 左側の数字が小さい順にペアを並べる
$(2,8)(1,4)(6,7)(3,5)$ を上記の規則に則って並べると、$(1,4)(2,8)(3,5)(6,7)$ です。
また、正規化された反転列の左側だけを抜き出したもの(今回だと $\{1,2,3,6\}$ )を左反転列と呼びましょう。
逆に考えてみる
さて、まだどのようにひっくり返せば ●○●●○○○● を全て白にできるのか見当がつきません。
そこで、 全て白のマス( ○○○○○○○○ )を手順にそってひっくり返すとどのようになるのかを、$N$ が小さい範囲で確かめます。
●○●●○○○● を ○○○○○○○○ にすることと、 ○○○○○○○○ を ●○●●○○○● にするのは互いに逆の関係にあります。
○○○○○○○○ を ●○●●○○○● にした後、同じ反転列でひっくり返すと ○○○○○○○○ に戻るからです。
N=1
$N=1$のとき、1通りのひっくり返し方があります。
N=2
$N=2$のときは、3通りのひっくり返し方がありますが、白黒パターンは2種類です。
N=3
$N=3$のときは、15通りのひっくり返し方があり、白黒パターンは5種類です。
規則の発見
ここまででいくつか発見があるので、まとめてみましょう。
最終的に白か黒かは下に引かれている線の数によって決まる
マスの下にある(もしくは自分自身からのびている)線の回数ひっくり返されるので、線の数によって最終的にマスが白になるか黒になるか決まります。
線の数が偶数のとき白、奇数のとき黒になります。
白黒パターンの両端は黒
両端は自身を選択した際にひっくり返され、他のマスに挟まれないので黒です。
クラスタに分かれたとき、各クラスタの両端は黒
クラスタに分かれる、というのは、以下のように全くある区間内で反転が完了している状態です。
クラスタに分かれたとき、各クラスタの両端は黒です。
各パターンの反転列を見ると、左反転列の数字が共通
$N=3$ で、白黒パターンごとの入れ替え列をまとめます。
白黒パターンごとに反転列をまとめると、白黒パターンごとに反転列の左右が同じことに気づきます。例えば、○○○○○○ を ●○○○○● にする反転列には、ペアの左側に$\{1,2,4\}$が現れ、右側に$\{3,5,6\}$が現れます。
重なり合う(L1, R1)(L2, R2)を(L1, R2)(L2, R1)に入れ替えても結果は同じ
下の2つの反転列 $(L_1, R_1)(L_2, R_2)$ と $(L_1, R_2)(L_2, R_1)$ の白黒パターンは同じです。マスの下の線の数が変わらないためです。
互いに線が交差しない反転列が各白黒パターンに1つだけ存在する
線が交差する、とは以下の状況を指します。
ひっくり返すペア同士を線で結んだ時、白黒パターンごとに1つだけ線が交差しない反転列があります。
$N=3$ の場合はそれぞれこの反転列です。
互いに線が交差しない反転列を無交差反転列と呼びましょう。
無交差反転列において、反転のペアは同じ色になる
無交差反転列において、線が繋がっているもの同士は操作終了後同じ色になります。互いに線が交差しない入れ替え列において、ひっくり返すペアは、それ以外のペアに囲まれているか、離れているかのどちらかなので、同時にひっくり返るか同時にひっくり返らないかのどちらかだからです。
隣同士のペアを見つける
無交差反転列では、値が隣同士のペアが少なくとも1つあります。そのペアは白黒パターンでは同じ色になっています。
マスを左から見ていくときに、色が違う場合は隣同士のペアではありません。
スタックに入れてペアを見つけよう
無交差反転列一覧をぼんやり眺めていると、数式のカッコの対応のように見えてきました。
このような対応関係を作成する場合はスタックを使います。
まずは隣同士のペアを見つけましょう。隣同士なので値が連続します。連続した色が見つかるまではスタックに積み上げていきましょう。
●○●●○○○● を例に考えます。
4番目の●はスタックの一番上と同じ色なので、スタックの一番上を取り出し、4番目とペアにします。

5番目の○はスタックの一番上と同じ色なので、スタックの一番上を取り出し、5番目とペアにします。

6番目の○はスタックの一番上と違う色なので、スタックに入れます。

7番目の○はスタックの一番上と同じ色なので、スタックの一番上を取り出し、7番目とペアにします。
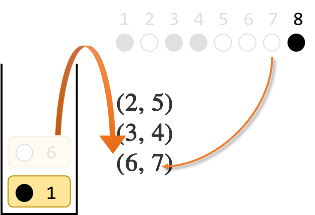
最後に、8番目の●はスタックの一番上と同じ色なので、スタックの一番上を取り出し、8番目とペアにします。

ここまでで ●○●●○○○● を ○○○○○○○○ にするには$(1,8)(2,5)(3,4)(6,7)$が1つの解であることがわかりました。実際に確かめて見ると、確かに全て白になります。
例外ケースの対応
上記は反転列が存在するケースですが、ここで例外もみておきます。
スタックの一番下が白
両端は黒でないと、全て白にすることができません。これを言い換えると、スタックに入れる時、一番下は黒でなければならない、となります。一番下に白が入るような入力が与えられた場合、全てのマスを白色にする方法は $0$ 通りです。
最後までマスを読んだときにスタックが空でない
最後までマスを読んだときにスタックが空でない場合は、与えられたパターンになる組み合わせは存在しません。この場合は全てのマスを白色にする方法は $0$ 通りです。
(L1, R1)(L2, R2)を(L1, R2)(L2, R1)に入れ替える場合の数
$(L_1, R_1)(L_2, R_2)$ を $(L_1, R_2)(L_2, R_1)$ に入れ替えても結果は同じです。$(1,8)(2,5)(3,4)(6,7)$ に対して、このような入れ替えが何パターンあるか考えます。
$(1, R_1)(2, R_2)(3,R_3 )(6, R_4)$
の $R_1$ から $R_4$ の部分に$\{4, 5, 7, 8\}$ を入れますが、 $L_i < R_i$ の制約があるので、$R_4$ から考えていきましょう。
$R_4$ : $7$ か $8$
$R_3$ : $4$, $5$, $7$, $8$ のうち1つ (ただし $R_4$ で使用した数字は含まない)
$R_2$ : $4$, $5$, $7$, $8$ (ただし $R_4$, $R_3$ で使用した数字は含まない)
$R_1$ : 残った数字1つ
これを計算すると、$2 \times 3 \times 2 = 12 通り$ です。
ひっくり返す順番の数を掛ける
ここまで、反転列は正規化されていますが、ひっくり返す順番は区別するので、$N!$を掛けます。
$ 12 \times 4! = 288 $
10000000007で割る
最後に、求めた数を $10^9+7$ で割ります。実際のプログラミングでは上記の組み合わせを計算する過程で$10^9+7$で適宜割り、桁があふれないように工夫します。
参考 : 「1000000007 で割ったあまり」の求め方を総特集! 〜 逆元から離散対数まで 〜 - Qiita
$ 288 \bmod (10^9+7) = 288$
答えの 288 が導かれました。
スタックは無くても解ける
今回はスタックを使用しましたが、スタックが無くても解けます。詳しくは本家の解説をご覧ください。
ソースコード
上記アルゴリズム(を改善したもの)をPython(バージョン3.7)で実装しました。($10^9+7$で割る前まで実装してあります。なので$N$が小さい範囲しか扱えません)
さらなる課題
$N$ 毎に、現れる白黒パターンは、
$N=1$ で $1$種類
$N=2$ で $2$種類
$N=3$ で $5$種類
あることがわかりました。$N=6, 7, 8$と数を大きくしていくとどうなるでしょうか?
あとがき
ざっと書いてみましたが、問題を本格的に考え始めてからアルゴリズムを思いつくまで3日かかりました。(最後ちょっとわからない部分があったので解説を見ました。)本家の解説よりだいぶ遠回りして解いていますが、そのぶん色んな発見があって楽しかったです。
コンテスト参加者はこんな問題をぱっと見で解いてるのかと思うと、末恐ろしいという浅い感想しか出てきません。




















