NetworkX という Python 向けの素敵なグラフライブラリを知ったので、練習がてら「ランダムグラフの最大連結部分のサイズがどんくらいになるか」という実験をしてみた。
(ここでの「グラフ」とは数値データを可視化する図のことではなく、ネットワークグラフ的な意味でのグラフ)
問題設定
- 頂点 (node) がN個ある。
- ランダムに2点を選んで辺 (edge) で結ぶ。これをS回繰り返す。
- 辺でつながった部分(連結部分)の最大サイズはいくらか。
この問題は S. Kauffman の著書「自己組織化と進化の論理」3章で紹介されたもので、多様な物質の混合物から生命が創発するモデルの一部として登場している。
コードと実行
ここでは networkx, numpy, matplotlib, および pydot をインスコしたものとする。インストール手順については最後に軽く触れる。
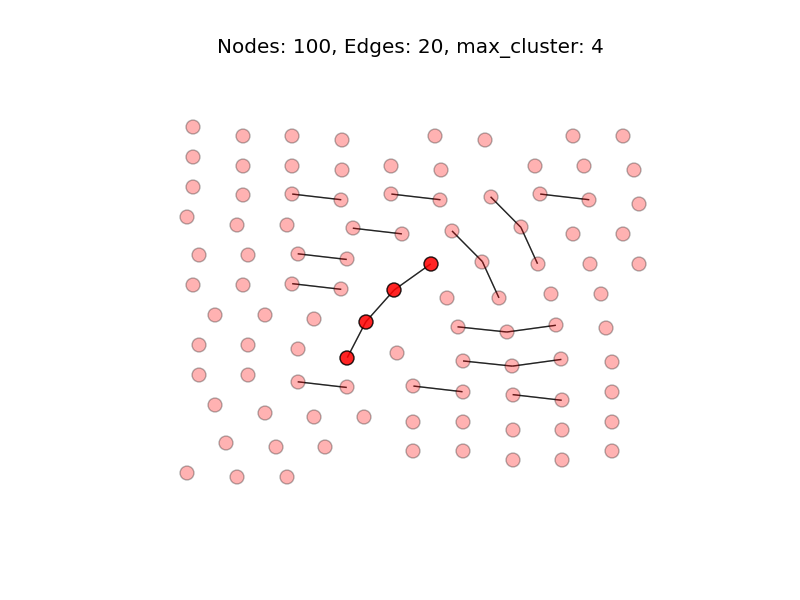
上記の問題に従い、ランダムに N=100 個のノード間に S=20 個の辺を引くコードを書いてみる。
import networkx as nx
import numpy as np
import matplotlib.pyplot as plt
N = 100 # number of nodes
S = 20 # number of edges
G = nx.Graph()
G.add_nodes_from(range(N))
G.add_edges_from(np.random.randint(N, size=(S,2)))
# get max connected component
max_size = 0
for component in nx.connected_components(G):
if len(component) > max_size:
max_cluster = component
max_size = len(max_cluster)
print max_cluster
# draw graph
plt.title("Nodes: {}, Edges: {}, max_cluster: {}".format(N, S, max_size))
nx.draw_graphviz(G, alpha=0.3, color='r', node_size=100)
nx.draw_graphviz(G, nodelist=max_cluster, alpha=0.8, color='b', node_size=100)
plt.show()
S=20 とした場合、最大の連結部分は4個にすぎない。
S=50 にするとずいぶん複雑なクラスタができてくる。最大サイズは15個。
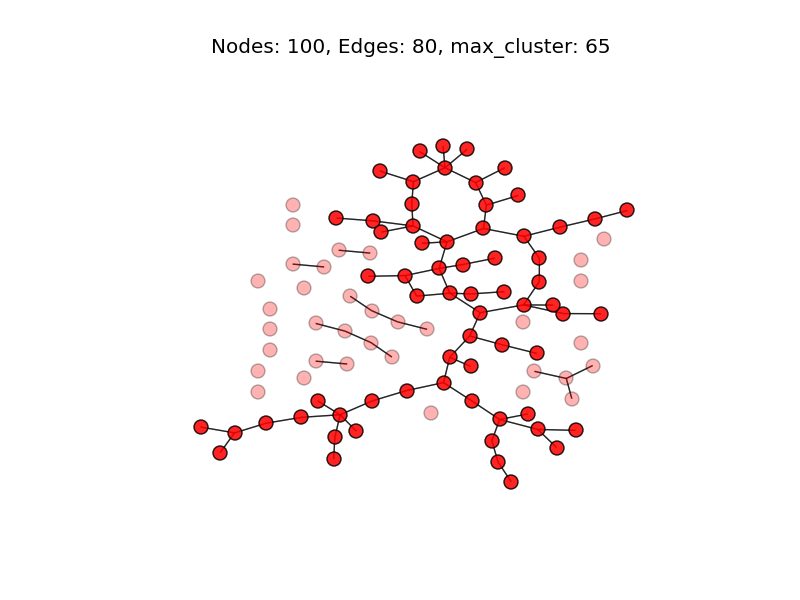
S=80 ともなれば、もはや半分以上の頂点が単一のクラスタに所属している。
次に N=1,000 に増やして、S と最大クラスタの相関を調べてみる。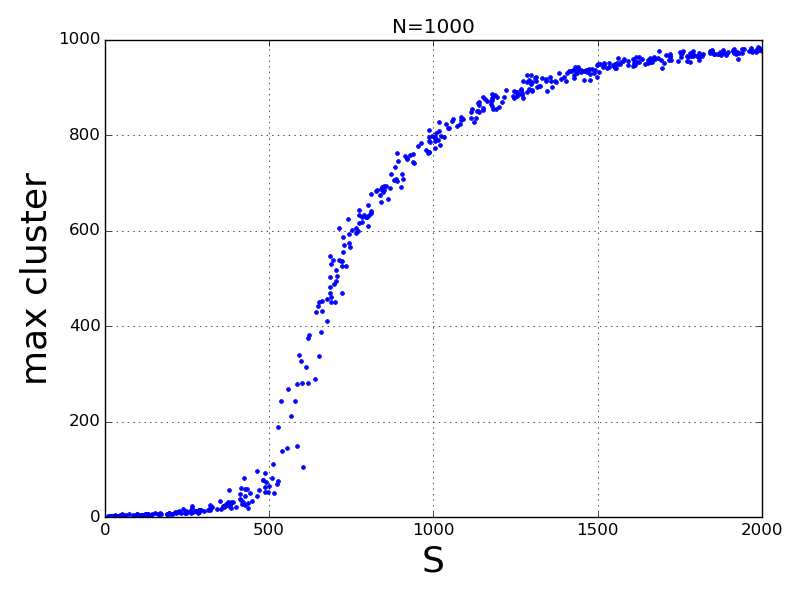
およそ S=500 のあたりで急速に max_cluster のサイズが増加してくることが分かる。
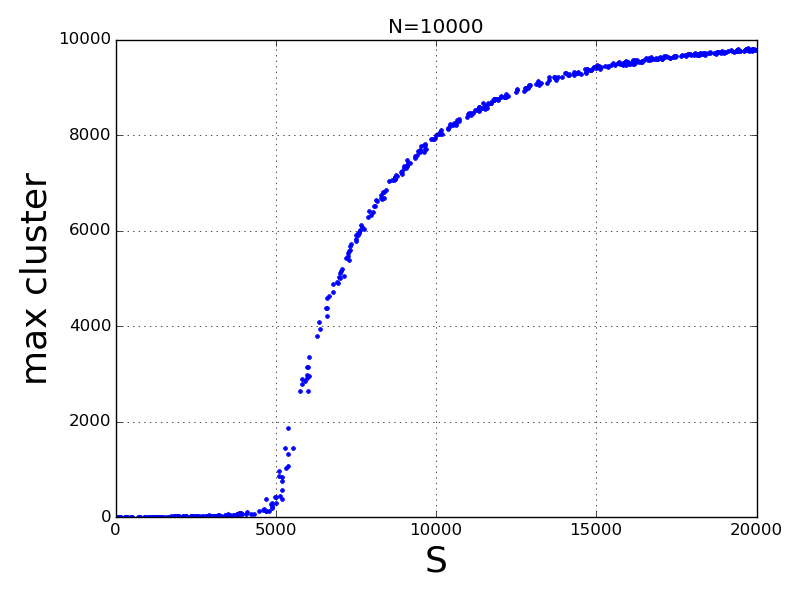
同様のことを N=10,000 で行う。
ほぼ同じ。S/N = 0.5 あたりで相転移的にクラスタが巨大化することが分かる。
インストールとか
NetworkX 自体は pip で簡単に
# pip install networkx
でインスコ出来る。グラフの可視化を綺麗にするには Graphviz というのを使うのが良くて、これは
# pip install pydot
で行けるんだが、なぜか僕の環境では実行時に
NameError: global name 'dot_parser' is not defined
というエラーが出た。調べてみると
http://stackoverflow.com/questions/15951748/pydot-and-graphviz-error-couldnt-import-dot-parser-loading-of-dot-files-will
pyparsing というライブラリのバージョンが 2.x になると動かなくなるらしい。以下の手順で 1.5.7 に戻す。
pip uninstall pyparsing
pip install -Iv https://pypi.python.org/packages/source/p/pyparsing/pyparsing-1.5.7.tar.gz#md5=9be0fcdcc595199c646ab317c1d9a709
pip install pydot