深層学習モデルを構築する時、うまく活性化関数を選ぶことは大事です。
前編に続き、もう一つ活性化関数Leaky ReLUについて紹介したいと思います。
Leaky ReLUとは?
Leaky ReLUはReLUの派生形の一つです。
数式を書くと
f(x) = max(ax, x)
ちなみに、$a$の数値は0.01で設定される場合が多いです。
数式により、$x$が負数の場合であれば$f(x)$は$ax$になるでしょう。
Pythonで書いてみると
def leaky_relu(x):
return max(0.01*x, x)
Leaky ReLUの微分
- $x$が正数の場合であれば:
\frac{\mathrm{d} f(x)}{\mathrm{d} x}=\frac{\mathrm{d} x}{\mathrm{d} x}=1
- $x$が$0$以下の場合であれば:
\frac{\mathrm{d} f(x)}{\mathrm{d} x}=\frac{\mathrm{d} ax}{\mathrm{d} x}=a
Pythonのif文で書いてみると
def leaky_relu_derivative(x):
if x >= 0 :
return 1
if x < 0 :
return 0.01
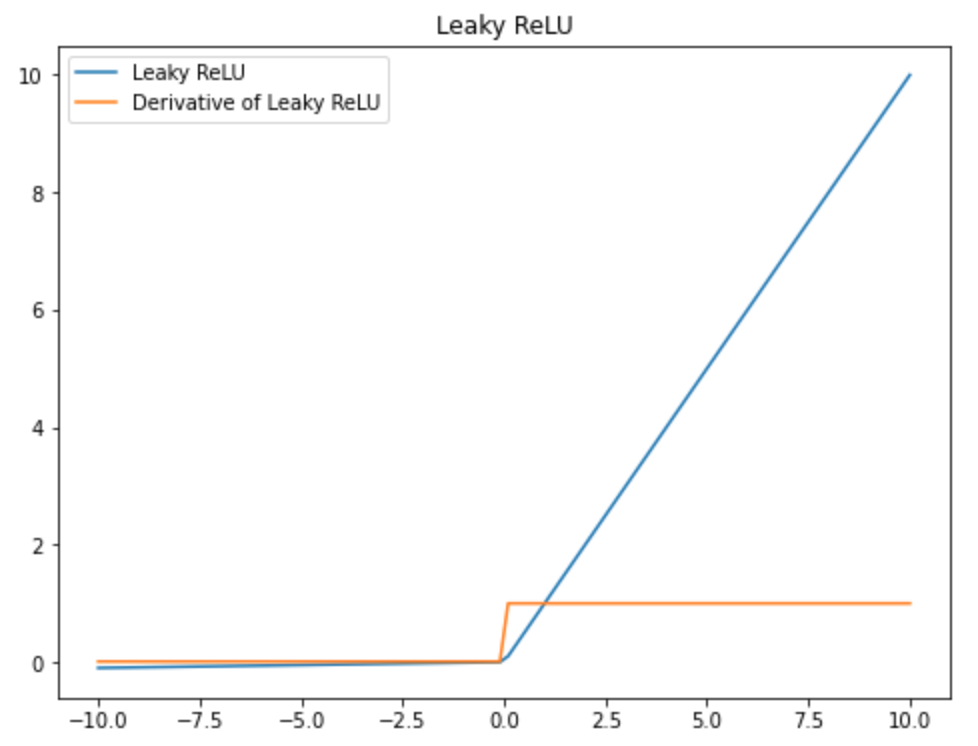
Leaky ReLUのグラフを作成
import numpy as np
import matplotlib.pyplot as plt
# inputデータ作成
X = np.linspace(-10, 10, 100)
plt.figure(figsize=(8,6))
plt.plot(x, list(map(lambda x: leaky_relu(x), X)), label="Leaky ReLU")
plt.plot(x, list(map(lambda x: leaky_relu_derivative(x), X)), label="Derivative of Leaky ReLU")
plt.title("Leaky ReLU")
plt.legend()
plt.show()
オレンジの線を見ると、
$x\ge0$の時、微分の数値は$1$で、
$x\lt 0$の時、微分の数値は$0$に近いですが、実は$0.01$です。
以上、簡単にメモしました。