はじめに
この記事はHoudini Apprentice Advent Calendar 2019の10日の記事となります。
はじめまして、yu_kitaと申します。初の投稿で緊張しておりますが頑張ります!
毎年のHoudini Advent Calendarが楽しみで、今年は自分も何か書いてみたいと思い今回挑戦してみた次第です。
今回はVEXで対数螺旋を作る方法をお話しできればと思っていますのでよろしくお願いします!
独学の部分も多くあり間違いなどもあるかもしれませんが、ご容赦ください。

対数螺旋とは
VEXでコードを記述する前にそもそもの対数螺旋を調べてみます。wikipedia先生お願いします。
対数螺旋(たいすうらせん、英: logarithmic spiral)とは、自然界によく見られる螺旋の一種である。
極座標表示 (r, θ) で r=ae^bθ と表される平面曲線を対数螺旋という。
有名なところだと、台風の渦やオウムガイの殻の形状だったりギリシャの建築でも見られるようですね。
式では指数が使われてますが、対数の方が先に認知されていたので対数螺旋と呼ぶようです。
極座標やら記号やらいろいろ出てきていますが一つずつみていきましょう
極座標
極座標ですが、原点からの距離rと角度θを与えてあげれば、ある一点の位置が求められます。
そして、その距離rに上記の式をあてはめれば対数螺旋としてあらわすことができると。
ちなみに三次元の場合はrとθに合わせてΦ(黄金比で使用しているΦとは関係ない)という三変数で位置を求めることになります。
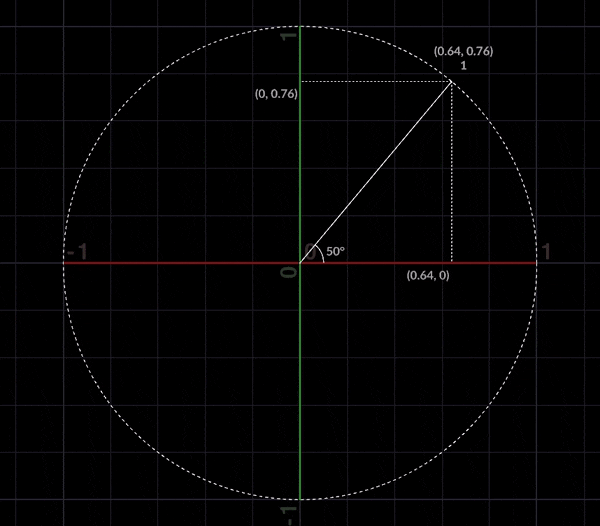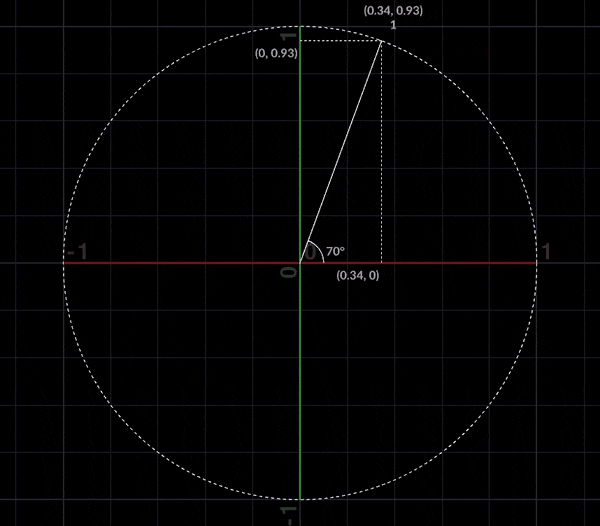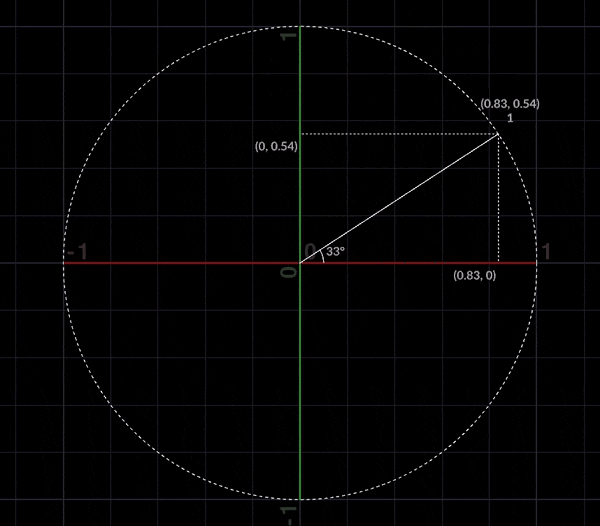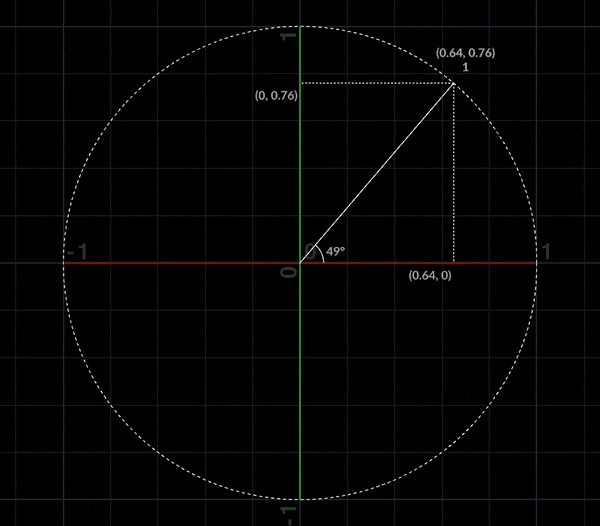
また極座標は直交座標にも変換する事が可能で
\displaylines{
x = rcosθ\\
y = rsinθ
}
とあらわす事ができます。これらをふまえて対数螺旋にいきましょう。
対数螺旋
では対数螺旋の式をあらためて。
r = ae^{bθ}
オエッなにやら色んな記号がでてきてますね。
それぞれがどんな意味を持っているのか見ていきましょう
| 記号 | 意味 |
|---|---|
| r | 原点からの距離 |
| θ | 角度(ラジアン) |
| e | 自然対数の底、ネイピア数 |
| a | スケール係数 |
| b | ピッチを決めるための要素 |
ここで対数螺旋の形をつくるうえで重要なのはbになります。
aは単純にスケール係数となるので拡大・回転による変化を考慮しなければ形に直接かかわりません。
rとθは極座標で位置を求めるための記号でしたし、eも微分・積分などでよく使われる記号で決まった値(2.718...)ですね。
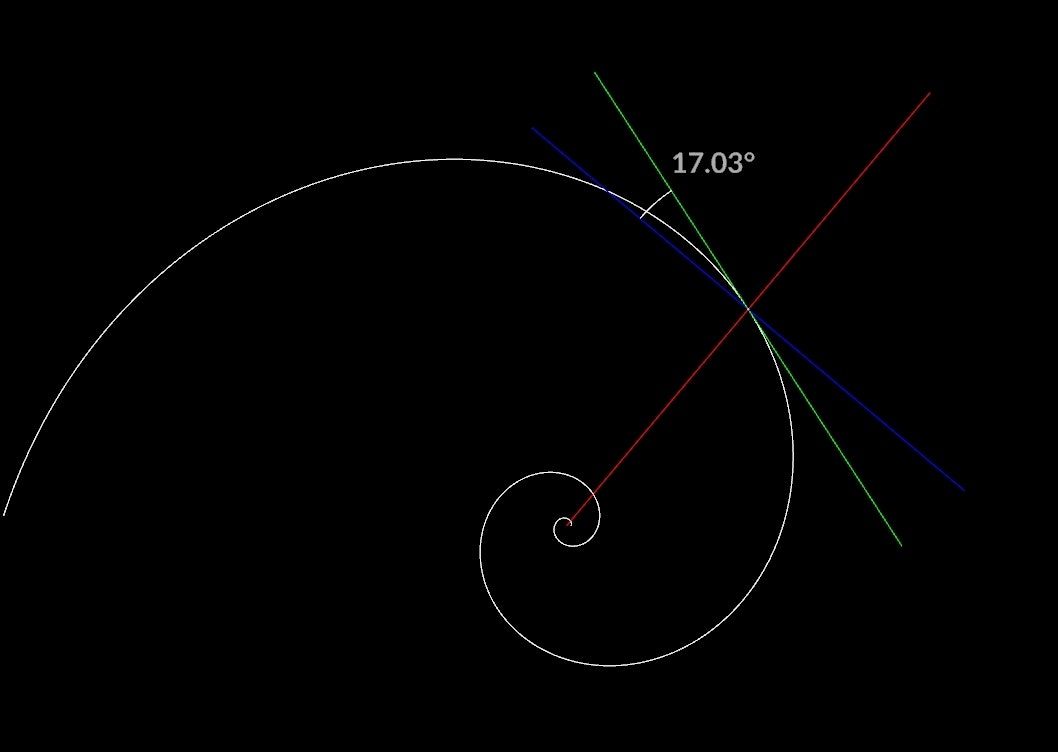
ピッチ
bについてもう少し。
bはピッチを決めるための要素であると書きましたが、そもそもピッチとはなんでしょうか?
簡単にいうとというか詳しくいえません...、
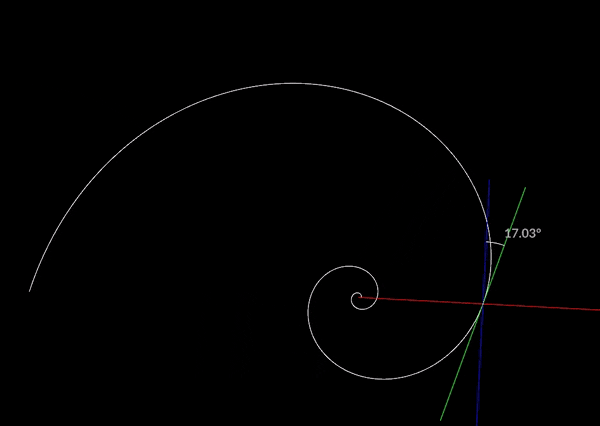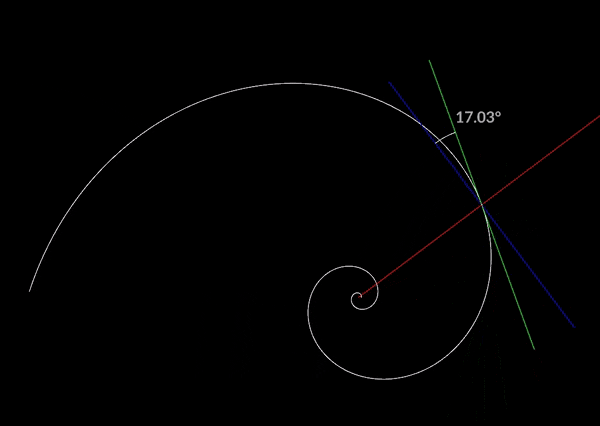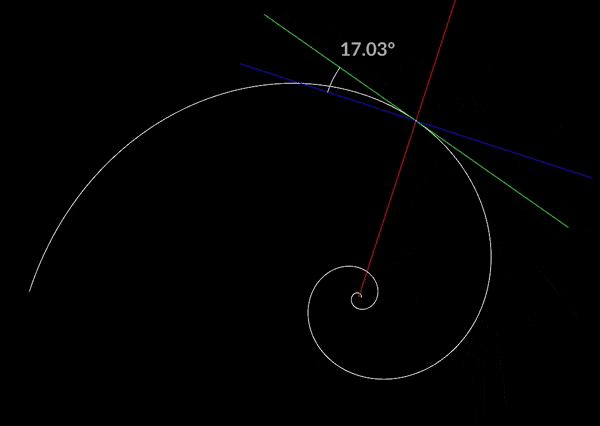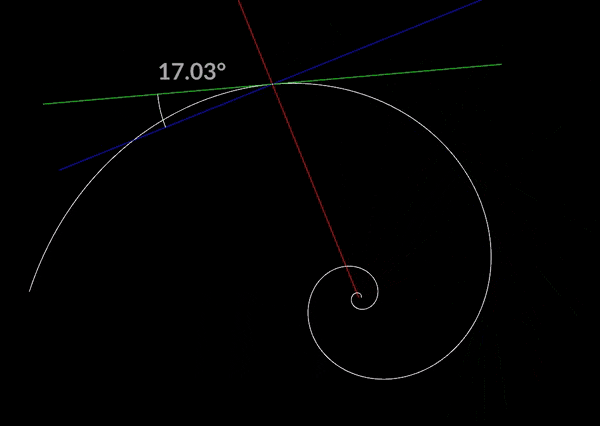
原点から任意の点に伸ばした直線の交点から垂直に伸ばした線と接線との角度の事をピッチと呼ぶようです。
この角度によって螺旋の巻き具合が変化し、それを決めるためにbを求めるということになります。
性質
等角
対数螺旋にはいくつか性質があり、一つ目がどの点においてもピッチが変化しないということです。
常に一定の角度を保つことから対数螺旋は等角螺旋とも呼ばれるようです。
自己相似
そしてもう一つが、自己相似と呼ばれる性質があります。wikipedia先生によると
任意の倍率で拡大または縮小したものは、適当な回転によって元の螺旋と一致する。
例えば、e2πb 倍に拡大したものは、回転することなしに元の螺旋と一致する。
下記の図だとΦ^4倍した時とΦ^2倍したものに対し180度回転させた時の螺旋が元の螺旋に一致してますね。

黄金螺旋
ではでは、今度は黄金比Φからbを求めていきましょう。bの式は下記になります。
\begin{align}
\phi &= \frac{1+\sqrt5}{2}\\
b &= \frac{\log_e\phi}{\pm\pi/2}\\
\end{align}
またかよ。 なにやらbにlogやらπやらがでてきてますね。そういう式なんだと思えばいいのですが、
できれば納得しておきたいところです。
この辺りは自分も理解が及ばず、あいまいな部分があるのですが、
90度(π/2)回転する毎にΦずつ螺旋が拡大すると考えて式を解いていこうと思います。
90度(π/2)でΦ倍されるので、360度(2π)でΦ^4倍だとすれば下記が成り立ちます。
\begin{align}
e^{b(θ{\pm}2\pi)} &= \phi^4 e^{bθ}\\
\end{align}
指数方程式より、等式において指数の底が同じであれば指数を外す事ができるのでまずは指数の底を揃えましょう。
底の異なるものは対数に変換する事で揃えられるので、それをふまえると
\begin{align}
e^{b(θ{\pm}2\pi)} &= \phi^4e^{bθ}\\
e^{b(θ{\pm}2\pi)} &= e^{\log_e\phi^4}e^{bθ}\\
e^{b(θ{\pm}2\pi)} &= e^{\log_e\phi^4 + bθ}\\
\end{align}
となります。底を揃える事ができたので、今度は指数を外してbについて解いていきましょう
真数にかかっている指数は手前にもっていく事ができるので
\begin{align}
b(θ{\pm}2\pi) &= \log_e\phi^4 + bθ\\
bθ{\pm}2{\pi}b &= 4\log_e\phi + bθ\\
{\pm}2{\pi}b &= 4\log_e\phi\\
\end{align}
\begin{align}
b &= \frac{4\log_e\phi}{{\pm}2{\pi}}\\
b &= \frac{\log_e\phi}{\pm\pi/2}\\
\end{align}
となり、黄金螺旋の式になりましたね!
ここまできたら実際にVEXで上記をあてはめていきましょう。
VEXで対数螺旋を作成
ようやくですがVEXで対数螺旋を作っていきましょう。あてはめるだけなのでさらりと。
今回bの値に黄金螺旋の式をいれていますが、他の値だとまた形が変わるので是非いれてみてください。
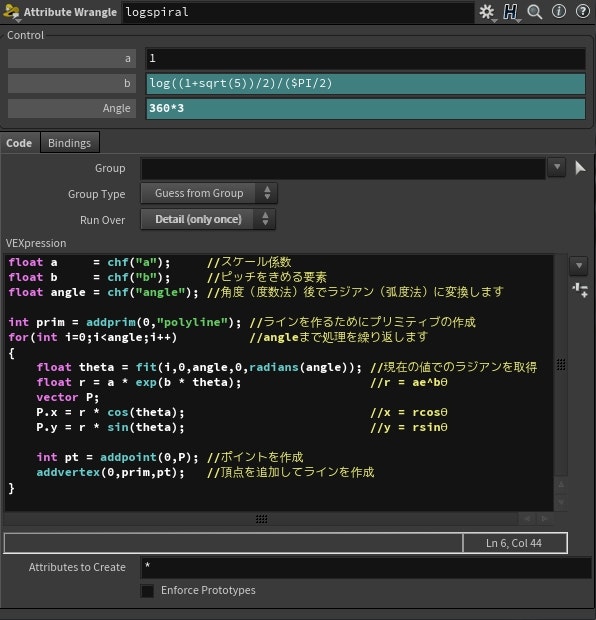

Snippet
float a = chf("a");
float b = chf("b");
float angle = chf("angle");
int prim = addprim(0,"polyline");
for(int i=0;i<angle;i++)
{
float theta = fit(i,0,angle,0,radians(angle));
float r = a * exp(b * theta);
vector P;
P.x = r * cos(theta);
P.y = r * sin(theta);
int pt = addpoint(0,P);
addvertex(0,prim,pt);
}