AR，AM，ARMAモデルへのフィッテング

はじめに

本稿では，pythonを用いて，与えられた時系列データをARモデル，AMモデル，ARMAモデルにフィッティングする方法を記述する．

用いる関数

関数statsmodels.tsa.arima_model.ARMA.fitを用いる．
詳細はこちら

ARモデルのフィッティング

例として，AR(1)モデルのフィッティングをする．

y_t = 1 + 0.5 y_{t-1} + \epsilon_t

ただし，$\epsilon_t$は分散1の正規ホワイトノイズとする．
また，$y_0=2$とする．

#モジュールの取り込みとグラフをいい感じにするおまじない
import matplotlib as mpl
import matplotlib.pyplot as plt
plt.style.use('seaborn')
mpl.rcParams['font.family'] = 'serif'
%matplotlib inline
import numpy as np
import statsmodels.api as sm
import statsmodels.tsa.api as smt
p = print

#プロットするデータ列の作成
#今回は1000個の時刻におけるデータを取り込む
y = np.zeros(1000)
np.random.seed(42)
epsilon = np.random.standard_normal(1000)
y[0] = 2
for t in range(1,1000):
    y[t] = 1 + 0.5 * y[t-1] + epsilon[t]

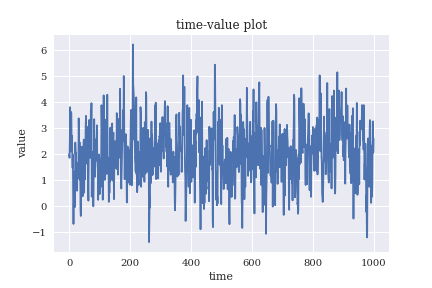
#プロットする時系列データを見てみる
plt.plot(y)
plt.xlabel('time')
plt.ylabel('value')
plt.title('time-value plot');

次のグラフがプロットされる．

このモデルをフィッティングする．

mdl = smt.ARMA(y, order=(1, 0)).fit()
p(mdl.summary())

結果は以下のようになる．

定数項は2.0336，ARモデルの係数は0.4930と実際の2，0.5と近い値を推定できていることがわかる．
また，今回のモデルは，定数項2を含んだARモデルであったが，定数項が0であることが既知である場合は，

mdl = smt.ARMA(y, order=(1, 0)).fit(trend='nc')

とすればよい．

MAモデルのフィッティング

order=，の部分の数字を変えるだけでよい．
例えば，MA(1)にフィッテングする場合は，

mdl = smt.ARMA(y, order=(0, 1)).fit()

とすればよい

ARMAモデルのフィッテング

ARMA(1, 1)にフィッテングする場合は，

mdl = smt.ARMA(y, order=(1, 1)).fit()

とすればよい

そもそもARMAの次数の検討がつかない場合

関数sm.tsa.arma_order_select_icを用いると，情報量基準で最適な次数を推定できる．
関数の詳細はこちら

ARMAモデルの次数推定

先に述べたAR(1)モデルモデルの時系列データを用いて，次数の推定を行います．
つまり，次数が(1,0)であると推定できれば成功です．

from statsmodels.tsa.arima_process import arma_generate_sample

y = np.zeros(1000)
np.random.seed(42)
epsilon = np.random.standard_normal(1000)
y[0] = 2
for t in range(1,1000):
    y[t] = 1 + 0.5 * y[t-1] + epsilon[t]

sm.tsa.arma_order_select_ic(y)

結果は以下のようになります．

次数(1,0)が最適に推定されました．
行列は，BICの値を表しており，
行がARの次数，列がAMの次数を表しています．

AICを用いたい場合や，AICとBICの両方で評価したい場合は以下のように記述します．

#AICを用いる場合
sm.tsa.arma_order_select_ic(y, ic='aic')
#2つの情報量基準で同時に評価したい場合
sm.tsa.arma_order_select_ic(y, ic=['aic', 'bic'])

また，次数の最大値を変更してサーベイしたり，定数項=0と仮定した上で推定することも可能です．