はじめに
製造業における設備の保全は、これまでの主流だったTime-Based Maintenanceから、Condition-Based Maintenance (CBM) やPredictive Maintenance (予知保全)にシフトしつつあります。その最初の一手として、「振動センサーによる回転機器の状態監視」に取り組まれている方もそれなりにおられることと思います。
基本的には、ベンダーのソリューションを買ってくれば、設備の健康状態を表示するダッシュボードは簡単に作れますし、スペクトルもボタン1つで作成できてしまいます。しかし、このあたりの技術を自分で手を動かしてちゃんと理解しておきたい、と思われる方もおられるかもしれません。そのような方向けに、周波数解析の方法をまとめておきたいと思います。みなさんの理解の一助になれば幸いです。
データ収集の概要
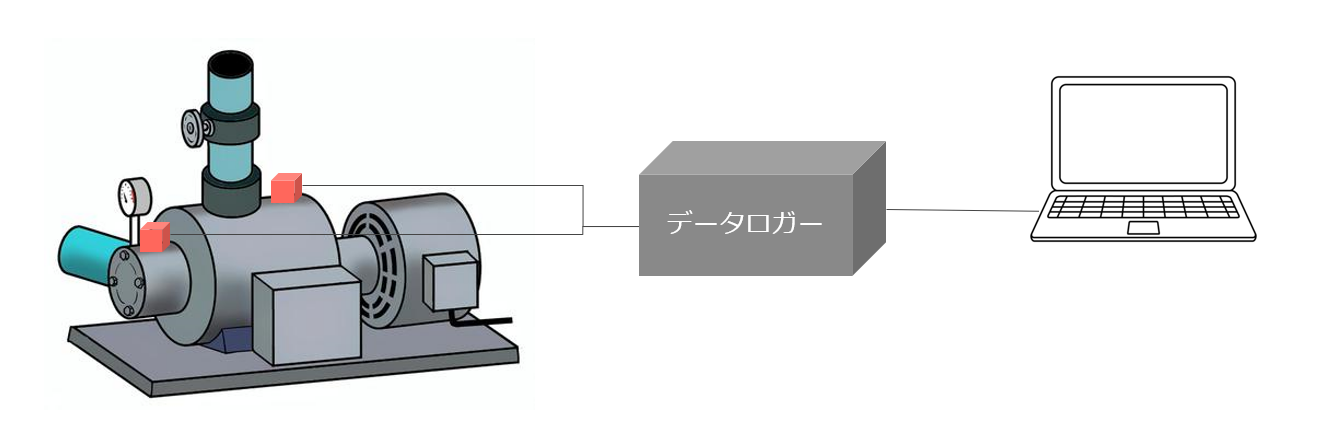
本記事で用いる振動データをどうやって収集したかを軽く紹介しておきます。 下のイラストに示したように、振動センサーを回転機器にとりつけ、データロガーにつなぎます。ロガーの出力はノートPCのハードディスクに書き込んでいきます。振動センサーのデータは、50 kHzのサンプリング周波数で5秒間収集しました。
少し脱線しますが、使用したセンサーやロガーなどのハードウェア情報を知りたい方はこちらをご参照ください。参考文献もいくつか挙げています。
解析するデータについて
データファイルは以下のような形式になっています。CH1, CH2,,,,は1つめの振動センサーのx成分、y成分、z成分、2つめの振動センサーのx成分、y成分、z成分です。単位は加速度なのでm/s^2です。
Time CH1 CH2 CH3 CH4 CH5 CH6
5:05:17.501 -2.25E+00 -1.21E+00 5.4167E-01 -6.04E-01 4.4167E+00 -2.25E+00
5:05:17.501 -2.08E+00 7.7083E-01 -2.50E-01 3.1458E+00 -2.10E+00 8.7500E-01
5:05:17.501 -2.54E+00 -1.21E+00 -1.21E+00 -3.13E-01 -1.40E+00 1.0625E+01
5:05:17.501 -1.67E+00 -1.35E+00 -9.58E-01 6.4375E+00 3.8542E+00 3.9167E+00
5:05:17.501 -1.15E+00 1.8750E-01 -1.17E+00 -2.29E-01 -3.06E+00 -3.58E+00
5:05:17.501 1.2292E+00 -1.77E+00 1.0833E+00 -8.96E-01 -3.15E+00 2.5000E+00
5:05:17.501 7.7083E-01 -1.85E+00 1.3333E+00 2.2500E+00 -9.38E-01 2.5000E-01
5:05:17.501 -4.17E-02 -2.31E+00 2.5000E+00 -2.29E-01 -1.67E-01 7.9167E-01
5:05:17.501 -6.04E-01 -3.90E+00 6.6667E+00 1.0208E+00 -4.17E-02 1.2500E-01
5:05:17.501 -9.17E-01 -1.88E+00 6.9583E+00 -2.25E+00 3.0417E+00 -6.38E+00
5:05:17.501 -9.17E-01 -2.04E+00 3.8333E+00 -1.25E+00 1.2500E-01 -1.71E+00
5:05:17.502 -2.15E+00 -2.15E+00 7.0833E-01 -2.38E+00 4.1667E-01 -1.25E+00
5:05:17.502 -1.92E+00 -2.92E-01 -4.17E+00 -2.96E+00 1.8125E+00 -1.33E+00
振動センサーからデータが取れるようになったら、時間 vs 振幅のプロットを作成して、回転機器の健康状態を監視しましょう。振動が徐々に大きくなりはじめたら、周波数解析を行ってスペクトルを導出し、その原因を突き止めることが次のステップとなります。
スペクトルの導出の流れ
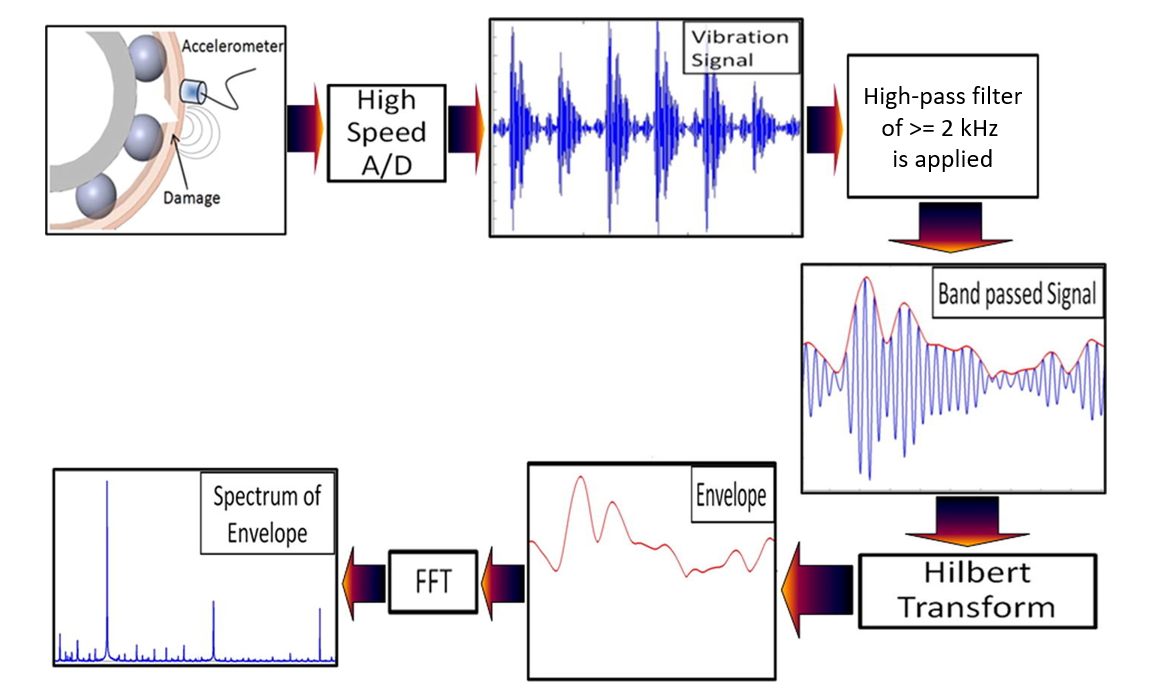
振動が大きくなる原因として、ベアリングの損傷による異常振動が最も疑われます。このような場合、数kHz以上の高周波成分のみを抽出する必要があるので、計測した生データをまずはHigh-pass filterにかけます。その後、ヒルベルト変換をかけてenvelop成分を抽出し、最後にFFTでスペクトルを導出する流れになります。単純に、波形データをフーリエ変換するだけではいけないのでご注意ください。この一連の流れを下に示しておきます (Tyagi & Panigrahi, 2017の図を一部修正して作成)。
実際の解析
以下にサンプルコードを示します。まずはhigh-pass filterのサンプルです。
#バターワースフィルタ(ハイパス)
def highpass(x, samplerate, fp, fs, gpass, gstop):
fn = samplerate / 2 #ナイキスト周波数
wp = fp / fn #ナイキスト周波数で通過域端周波数を正規化
ws = fs / fn #ナイキスト周波数で阻止域端周波数を正規化
N, Wn = signal.buttord(wp, ws, gpass, gstop) #オーダーとバターワースの正規化周波数を計算
b, a = signal.butter(N, Wn, "high") #フィルタ伝達関数の分子と分母を計算
y = signal.filtfilt(b, a, x) #信号に対してフィルタをかける
return y #フィルタ後の信号を返す
次はFFTのサンプルです。このページを参考に作成したようです。今見返しても、わかりやすいページですね。
#
# Refer the following page
# https://rikei-fufu.com/2020/06/27/post-3237-python-fft/
#
import numpy as np
import matplotlib.pyplot as plt
def FFT_main(t, x, dt, split_t_r, overlap, window_F, output_FN, y_label, y_unit):
#データをオーバーラップして分割する。
split_data = data_split(t, x, split_t_r, overlap)
#FFTを行う。
FFT_result_list = []
for split_data_cont in split_data:
FFT_result_cont = FFT(split_data_cont, dt, window_F)
FFT_result_list.append(FFT_result_cont)
#平均化
fq_ave = FFT_result_list[0][0]
F_abs_amp_ave = np.zeros(len(fq_ave))
for i in range(len(FFT_result_list)):
F_abs_amp_ave = F_abs_amp_ave + FFT_result_list[i][1]
F_abs_amp_ave = F_abs_amp_ave/(i+1)
return fq_ave, F_abs_amp_ave
def FFT(data_input, dt, window_F):
N = len(data_input[0])
#窓の用意
if window_F == "hanning":
window = np.hanning(N) # ハニング窓
elif window_F == "hamming":
window = np.hamming(N) # ハミング窓
elif window_F == "blackman":
window = np.blackman(N) # ブラックマン窓
else:
print("Error: input window function name is not sapported. Your input: ", window_F)
print("Hanning window function is used.")
hanning = np.hanning(N) # ハニング窓
#窓関数後の信号
x_windowed = data_input[1]*window
#FFT計算
F = np.fft.fft(x_windowed)
F_abs = np.abs(F)
F_abs_amp = F_abs / N * 2
fq = np.linspace(0, 1.0/dt, N)
#窓補正
acf=1/(sum(window)/N)
F_abs_amp = acf*F_abs_amp
#ナイキスト定数まで抽出
fq_out = fq[:int(N/2)+1]
F_abs_amp_out = F_abs_amp[:int(N/2)+1]
return [fq_out, F_abs_amp_out]
def data_split(t, x, split_t_r, overlap):
split_data = []
one_frame_N = int(len(t)*split_t_r) #1フレームのサンプル数
overlap_N = int(one_frame_N*overlap) #オーバーラップするサンプル数
start_S = 0
end_S = start_S + one_frame_N
while True:
t_cont = t[start_S:end_S]
x_cont = x[start_S:end_S]
split_data.append([t_cont, x_cont])
start_S = start_S + (one_frame_N - overlap_N)
end_S = start_S + one_frame_N
if end_S > len(t):
break
return np.array(split_data)
最後にmain文です。なお、ヒルベルト変換は、scipy.signal (Scipyの信号処理モジュール)を使うと、hilbert()でたった1行でやってくれます。scipy万歳。
import numpy as np
from scipy import signal
col_list = ['col1', 'col2', 'col3', 'col4', 'col5', 'col6', 'col7', 'col8', 'col9', 'col10', 'col11', 'col12']
### Parameter settings ###
samplerate = 50000
dt = 1.0/samplerate
t = np.arange(0, 5.0, dt)
split_t_r = 0.2 #1つの枠で全体のどの割合のデータを分析するか。
overlap = 0.5 #オーバーラップ率
window_F = "hanning" #窓関数選択: hanning, hamming, blackman
y_label = "amplitude"
y_unit = "V"
output_FN = "test.png"
fp = 2000 #通過域端周波数[Hz]
fs = 1000 #阻止域端周波数[Hz]
gpass = 3 #通過域端最大損失[dB]
gstop = 40 #阻止域端最小損失[dB]
### Parameter settings END ###
filepath = '.'
filepath2 = filepath + '/' + '20221103_175522_650.CSV'
filelist = glob.glob(filepath2)
spec_list = []
df = pd.read_csv(file, delimiter=',', header=None, skiprows=16, names=['stime', 'col1', 'col2', 'col3', 'col4', 'col5', 'col6', 'col7', 'col8', 'col9', 'col10', 'col11', 'col12'], index_col=False)
obs_time = file.split('_')[2][0:2] + ':' + file.split('_')[2][2:4] + ':' + file.split('_')[2][4:6]
sr1 = pd.Series(name='date', dtype='string')
sr2 = pd.Series(name='time', dtype='string')
sr3 = pd.Series(name='col_num', dtype='string')
for j, colname in enumerate(col_list):
x = signal.hilbert(np.abs(highpass(df.iloc[:, j+1].values[:250000], samplerate, fp, fs, gpass, gstop)))
aa, bb = FFT_main(t, x, dt, split_t_r, overlap, window_F, output_FN, y_label, y_unit)
sr1.loc[0+j] = dirname
sr2.loc[0+j] = obs_time
sr3.loc[0+j] = colname
spec_list.append(bb[:1500])
df_sum = pd.DataFrame(spec_list)
df_final = pd.concat([sr1, sr2, sr3, df_sum], axis=1)
df_final.to_csv("aaa.csv")
これで、得られたスペクトルがaaa.csvに保存されました。おつかれさまでした。
スペクトルを見てみましょう
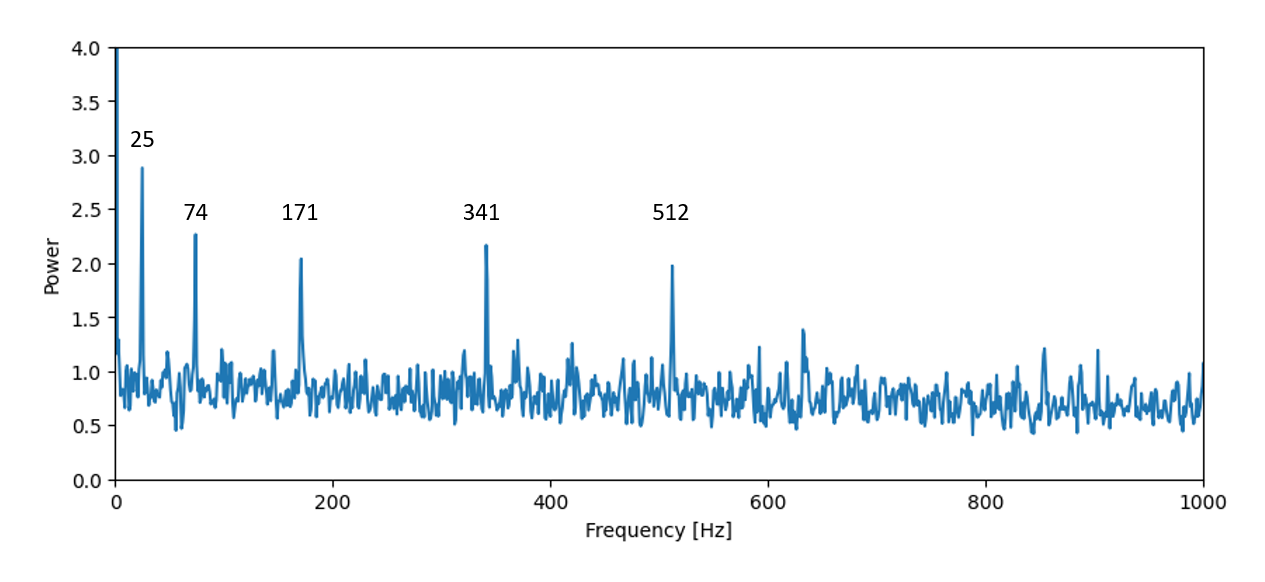
得られたスペクトルをプロットしたのが下図です。いくつかのピークがきれいに見えていますね。対応する周波数も追記しておきました。
長くなりましたので今日はこの辺で。これらのピークが何を示すかは、次の記事で調べてみましょう。