この記事は，2007年に万能チューリングマシンを構成できることが証明された『Wolfram's 2-state 3-symbol Turing Machine』をPython 3で簡易実装した例について，チューリングマシンの万能性や万能チューリングマシンの概要と共に述べています．名称としては長いので，ここでは『(2,3)TM』と略記することとし，日本語訳として『2状態3記号チューリングマシン』を用いることにします．詳細は次のページを御参照下さい．

Wolfram Research: Wolfram 2,3 Turing Machine Research Prize
Wikipedia: Wolfram's 2-state 3-symbol Turing machine

記事の目的は次のふたつです¹．

万能チューリングマシンとして構成された(2,3)TMの実装を通して，現代のプログラム内蔵型デジタルコンピュータの理論的な裏付けについて理解を深める．
万能チューリングマシンとして構成できる最も小規模なチューリングマシンと考えられている(2,3)TMの実装を通して，他の様々な仕組みで万能チューリングマシンを実装するための参考とする．

次の動画は，今回作成したプログラムのひとつを修正したものの実行デモです．

チューリングマシンの万能性

チューリングマシンとは，簡単に言えば，あらゆる計算が可能な自動機械の数学モデルのひとつです．アラン・チューリング（Alan Turing）氏が計算可能性理論における停止性問題を議論するため1936年に提案したモデルですが，結果的に，現代のプログラム内蔵型デジタルコンピュータの原理の理論的な裏付けのひとつとして位置付けられています²．

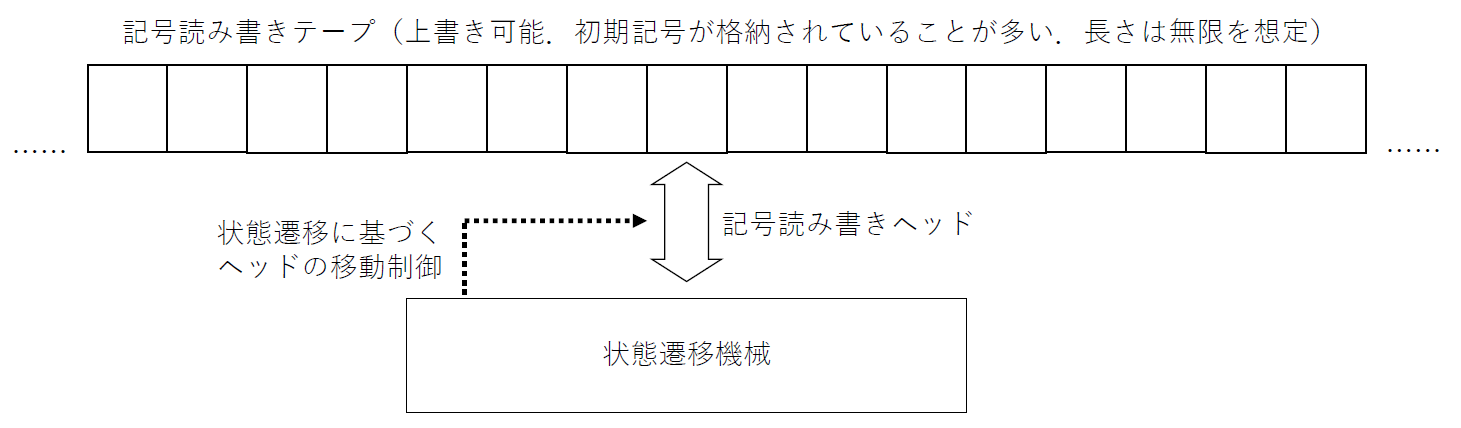
チューリングマシンは，記号の読み書きが可能な無限長のテープ，テープ対して記号を読み書きするヘッド，記号を読み書きしながらヘッドの位置を移動させることも可能な状態遷移機械から構成されています³．

上記のチューリングマシンの構成に沿ってPython 3で記述した例が次のプログラムです．

tm-framework.py

delta = # 状態遷移定義：(状態, 記号) -> (状態, 記号, ヘッド移動)

state = # 初期状態
tape  = # 初期テープ
head  = # ヘッダの初期位置

while True:
    if tape[head] == 停止記号: break
    t = delta[state][tape[head]]
    state = t[0]
    tape[head] = t[1]
    head += t[2]
    #print(tape)

この記述に沿った，1ビット同士の足し算を行うチューリングマシンの実装例は次の通りです．ただし，二進数計算ではなく，1+1=2であり，扱う記号は0,1,2の値と停止記号9を想定しています．入力ビットをテープの1番目と2番目に，停止記号9をテープの3番目にセットして実行すると，計算結果がテープの2番目に格納されて終了します．このため，テープ長は当初より有限（3）です．

tm-add.py

# 状態遷移定義：(状態, 記号) -> (状態, 記号, ヘッド移動)
delta = {0: {0: (0, 0, 1), 1: (1, 1, 1)},
         1: {0: (0, 1, 1), 1: (0, 2, 1)}}

# 初期状態
state = 0
# 初期テープ
di = input().rstrip().split()
tape  = [int(di[0]), int(di[1]), 9]
# ヘッダの初期位置
head  = 0

while True:
    if tape[head] == 9: break
    t = delta[state][tape[head]]
    state = t[0]
    tape[head] = t[1]
    head += t[2]
    print(tape)

print(tape[1])

（UNIXシェル上で実行）

$ python3 tm-add.py
0 0
[0, 0, 9]
[0, 0, 9]
0
$ python3 tm-add.py
0 1
[0, 1, 9]
[0, 1, 9]
1
$ python3 tm-add.py
1 0
[1, 0, 9]
[1, 1, 9]
1
$ python3 tm-add.py
1 1
[1, 1, 9]
[1, 2, 9]
2

初期状態と初期テープに対する計算手順は状態遷移定義で決まります．上記の場合，読み込まれる状態・記号と書き出される記号の関係が，1ビット同士の足し算を行う真理値表となっています（ただし，読み込まれる2ビットが同時読み込みではなく順次読み込みとする必要があることから，状態遷移によって1ビット目の情報を保持するようにしています）．次は，状態遷移定義を一覧にしたものです．

(現在の状態, 読み込み記号)	⇒	(遷移する状態, 書き出し記号, ヘッド移動)
(状態0, 記号0)		(状態0, 記号0, 右に1)
(状態0, 記号1)		(状態1, 記号1, 右に1)
(状態1, 記号0)		(状態0, 記号1, 右に1)
(状態1, 記号1)		(状態1, 記号2, 右に1)

証明は省きますが，チューリングマシンは，状態遷移と初期状態，初期テープの設定によって，数学的な事柄を扱うための手順全て，すなわち，あらゆる計算を表現できます．これは，チューリングマシンの万能性と呼ばれています．

万能チューリングマシンと(2,3)TM

万能チューリングマシンとは，あらゆるチューリングマシンを模倣することが可能なチューリングマシンを指します．具体的には，初期状態と初期テープの設定のみであらゆるチューリングマシンが模倣できるよう，状態遷移機械を設定・構築したチューリングマシンとなります．

2007年にWolfram Researchより，2つの状態と3つの記号のみで構成されたチューリングマシンについて，次の状態遷移によって万能チューリングマシンが構成できるか否かが証明問題として示され，同年に証明されました．このチューリングマシン（この記事では (2,3)TM と略記）は，現時点で最も小規模な万能チューリングマシンであると考えられています．なお，ここでは，2つの状態を0と1，3つの記号を0,1,2で表現しています．

(現在の状態, 読み込み記号)	⇒	(遷移する状態, 書き出し記号, ヘッド移動)
(状態0, 記号0)		(状態1, 記号1, 右に1)
(状態0, 記号1)		(状態0, 記号2, 左に1)
(状態0, 記号2)		(状態0, 記号1, 左に1)
(状態1, 記号0)		(状態0, 記号2, 左に1)
(状態1, 記号1)		(状態1, 記号2, 右に1)
(状態1, 記号2)		(状態0, 記号0, 右に1)

次は，上記の状態遷移を設定したチューリングマシンのプログラム例です．初期状態を0，初期テープを有限の長さ6として記号0で初期化した後，20ステップ実行します．

w23tm.py

# 状態遷移定義：(状態, 記号) -> (状態, 記号, ヘッド移動)
delta = {0: {0: (1, 1, 1), 1: (0, 2,-1), 2: (0, 1,-1)},
         1: {0: (0, 2,-1), 1: (1, 2, 1), 2: (0, 0, 1)}}

# 初期状態
state = 0
# 初期テープ
tape  = [0] * 6
# ヘッダの初期位置
head  = 2

print(tape)
for _ in range(20):
    t = delta[state][tape[head]]
    state = t[0]
    tape[head] = t[1]
    head += t[2]
    print(tape)

（UNIXシェル上で実行）

$ python3 w23tm.py
[0, 0, 0, 0, 0, 0]
[0, 0, 1, 0, 0, 0]
[0, 0, 1, 2, 0, 0]
[0, 0, 2, 2, 0, 0]
[0, 1, 2, 2, 0, 0]
[0, 1, 0, 2, 0, 0]
[0, 1, 0, 1, 0, 0]
[0, 1, 1, 1, 0, 0]
[0, 1, 1, 2, 0, 0]
[0, 1, 1, 2, 2, 0]
[0, 1, 1, 1, 2, 0]
[0, 1, 2, 1, 2, 0]
[0, 2, 2, 1, 2, 0]
[1, 2, 2, 1, 2, 0]
[1, 0, 2, 1, 2, 0]
[1, 0, 1, 1, 2, 0]
[1, 1, 1, 1, 2, 0]
[1, 1, 2, 1, 2, 0]
[1, 1, 2, 2, 2, 0]
[1, 1, 2, 2, 0, 0]
[1, 1, 2, 2, 0, 1]

この初期設定はテープ記号の書き換えを非周期的に行い，その書き換え範囲もテープ長の範囲で無限に増殖します．記事冒頭で示した動画は，このプログラムのテープ長を80とし，更に，記号0,1,2をそれぞれ空白，ピリオド，アスタリスクに置き換えて1ステップごとにテープの中身を表示させたものです．

次は，1ビット同士の足し算を行う（上記の状態遷移を用いた）(2,3)TMの初期設定の例です．先のチューリングマシンと同じく，二進数計算ではなく1+1=2であり，扱う記号は0,1,2の値です．ただし，(2,3)TMは停止記号を想定していないため，3ステップで求まることを想定しています．入力ビットをテープの2番目と3番目にセットして3ステップ実行すると，計算結果がテープの2番目に格納されて終了します．テープ長は，計算に必要な長さである4に固定しています．

w23tm.py

delta = {0: {0: (1, 1, 1), 1: (0, 2,-1), 2: (0, 1,-1)},
         1: {0: (0, 2,-1), 1: (1, 2, 1), 2: (0, 0, 1)}}

# 初期状態
state = 0
# 初期テープ
di = input().rstrip().split()
tape = [0, int(di[0]), int(di[1]), 0]
# ヘッダの初期位置
head  = 2

print(tape)
for _ in range(3):
    t = delta[state][tape[head]]
    state = t[0]
    tape[head] = t[1]
    head += t[2]
    print(tape)

print(tape[1])

（UNIXシェル上で実行）

$ python3 w23tm-add.py
0 0
[0, 0, 0, 0]
[0, 0, 1, 0]
[0, 0, 1, 2]
[0, 0, 2, 2]
0
$ python3 w23tm-add.py
0 1
[0, 0, 1, 0]
[0, 0, 2, 0]
[0, 1, 2, 0]
[0, 1, 0, 0]
1
$ python3 w23tm-add.py
1 0
[0, 1, 0, 0]
[0, 1, 1, 0]
[0, 1, 1, 2]
[0, 1, 2, 2]
1
$ python3 w23tm-add.py
1 1
[0, 1, 1, 0]
[0, 1, 2, 0]
[0, 2, 2, 0]
[1, 2, 2, 0]
2

上記の例は，万能チューリングマシンとしての(2,3)TMが，初期状態と初期テープの設定のみで，他のチューリングマシンと同等の計算を実装したことを示しています．

備考

記事に関する補足

今回の話題と『チューリングテスト』は全く関係ないです．
(2,3)TMが万能チューリングマシンになるなら，それを用いて万能チューリングマシンとしての(2,3)TMそのものもエミュレートできるはずだけど……Brainf*ckでBrainf*ckを実装するより面倒そうだなあ．
万能チューリングマシンと同等の計算能力をもつことは『チューリング完全』であると呼ばれていますが，元の英語表現であるTuring Completeをそのまま解釈するならば『チューリング完備』の方がいいんじゃないかなあ．ということもあって，この記事の本文ではチューリング完全/Turing Completeという言葉を使用していません．

更新履歴

2022-12-02：初版公開

後者は，ある仕組みで(2,3)TMによる万能チューリングマシンが実装できることを示すことで，その仕組みもまた万能チューリングマシンである可能性が高いことを示すことを想定しています． ↩
ここでいう『計算（computation）』は，数値的な演算（calculation）だけでなく，数学的な事柄を扱うための手順全てを含みます． ↩
句構造文法の制約に基づく言語処理の仕組みと等価であることから，そのことを意識して，読み出し専用のテープを別途想定する場合もあります．ただし，プログラミング言語の処理については，CやLISPにおけるマクロのように，プログラムそのものを書き換えながら実行する場合もあるため，読み書きテープのみの構成の方がより適切と言えるかもしれません． ↩

Wolfram's 2-state 3-symbol Turing Machineの実装例（Python版）

チューリングマシンの万能性

万能チューリングマシンと(2,3)TM

備考

記事に関する補足

更新履歴