オッズ比とは
オッズとは、ある事象が起こった確率を起こらない確率で割ったものです。
オッズ比とは、2つのオッズの比です。オッズ比は2×2のクロス表から計算でき、2つの要因間である結果の起こりやすさが何倍異なるのかを表します。以下の表で、オッズ比は、ad/bcで求められます。端的にいうと、オッズ比から、ある症状のある人(暴露ありの人)が症状のない(暴露なしの)人に比べて何倍病気にかかるのかが分かるのです。
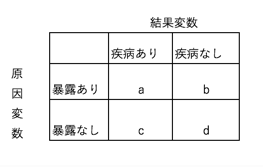
オッズ比は、暴露ありの人の中で病気にかかった人(a)/暴露ありの人で病気にかからなかった人(b)を、暴露なしの人で病気にかかった人(c)/暴露なしの人で病気にかからなかった人(d) で割った値です。(a/b)÷(c/d) なので、ad/bc です。分母は暴露なしの方をとり、暴露なしを基準とした時の暴露ありの病気のかかりやすさが何倍かを示しています。
オッズ比が1なら、暴露ありと暴露なしの差はない=>暴露ありは疾病の原因ではないと解釈し、オッズ比が3なら、暴露ありは暴露なしに対して3倍病気にかかっているので「暴露あり」は病気の原因だと解釈します。
オッズ比は0以上の値を取り上限は特にありません。複数の要因となる変数と結果との関係を検討する時、どの変数が結果に対してより強く影響力をもつかを比較して説明変数の絞りこみを行う際に有効な指標です。
Rで求めるオッズ比
Rでオッズ比を求めるパッケージは、fisher.test、Epiパッケージ、epitoolsパッケージ(このサイトに詳しいです)など複数ありますが、今回はオッズ比の信頼区間、p値も一緒に求められるEpiのtwoby2関数を紹介します。
Rのオッズ比の計算では、最も小さい値にコードづけされているカテゴリが基準となります※1)。男性を1,女性を0というコードに割り振ったら、値が0である女性を基準とした場合の男性のオッズ比が計算されます。
バイナリデータ準備
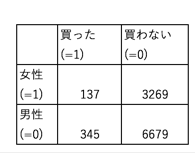
以下のような顧客の購買データを考えます。このような0と1からなるデータをバイナリデータセットとかダミーデータセットと呼びます。各変数(シュークリーム、オペラ、マカロンなど)には、買った人には1を、買っていないには0を入力しています。「女性」という変数では、女性=1,男性=0をコーディングしています。
Rでオッズ比を求める
ここで、シュークリームの購買と性別の関係をオッズ比から探ってみます。「シュークリームを買った」という「結果」に対して、性別「女性」がどれだけ効いているのかを知りたいとき、以下のように要因変数を行、結果変数を列にとったクロス表を作成します。
# データを読み込み
koubaidat<-read.table("koubaidata.dat",header=T)
cross<-xtabs(~女性+シュークリーム,data=koubaidat)
cross
twoby2(cross)
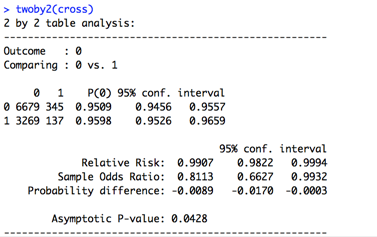
オッズ比は、Sample Odds Ratio:0.8113となりました。
上のクロス表では要因変数(女性)の基準カテゴリは0(男性)となっていて、結果変数(シュークリーム買う)も基準カテゴリは0(「買わない人」)になっています。そのため「買っていない人」の特徴を議論しており、女性に対して「男性は」0.8倍「買っていない」という解釈になります。
今度はクロス表のカテゴリを↓のような形に入れ替えます。これで買わない人の特徴ではなくて買った人の特徴を議論できるし、変数名にした「女性」が男性に比べて何倍なのかが分かります。
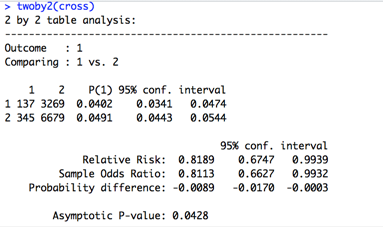
Rでクロス表を作ると自動的に0、1の順にカテゴリを並べるので、0を2にリコードしました。買った=1のまま、買わない=2、女性=1のまま、男性=2とリコードしたクロス表に対してオッズ比を求めます。
オッズ比は同じ0.8113でした。行と列の変数のカテゴリをそれぞれ入れ替えるということは、aとdをそしてbとcを入れ替えることになりますが、入れ替えてもad/bcの値は変わりませんね。
今度は、比較対象の男性に対して「女性は」0.8倍シュークリームを「買っている」と解釈できます。オッズ比が1以下なので、日本語では「女性は男性の0.8倍しかシュークリームを買っていない」となります。
最初のクロス表のオッズ比の解釈:女性に比べて男性は0.8倍シュークリームを「買ってない」ーーー>分かりにくい。
2番目のクロス表のオッズ比の解釈:男性に比べて女性は0.8倍シュークリームを「買っている」
2つは同じことなのです。
ダミー変数のオッズ比の解釈
Rのパッケージでダミー変数行列に対してオッズ比を求める時、データセットのカテゴリの0を(1より大きな値である)2とリコードする必要はありません。その結果を解釈する時に、要因の2群の比較を行う「カテゴリ1に比べて0は」の部分を「カテゴリ0に比べて1は」と読みかえ、結果変数に対しては「カテゴリ0である」を「カテゴリ1である」と読みかえればよい、ということになります。
参考になるリンク
※1岡田昌史編『The R Bookーデータ解析環境Rの活用事例集』(九天社)