R 大量のカテゴリ変数から変数間の連関度を表すクラメールV指標を計算し、有意で連関があるペアのみ抽出する

##目的

大量のカテゴリ変数からなるデータセットから、関連の強いとみられる変数ペアをクラメールV連関係数により探索します。カテゴリデータのクロス表の統計量には、χ2値、ファイ係数、クラメールV連関係数などがありますが、今回は、Rのvcdパッケージのassocstat関数を使い、データフレーム内の変数間のクラメールV係数を一気に求め、連関度が強く有意な変数間のペアのみ抽出します。

##想定
連関度が高いと判断する閾値：クラメールV0.3以上(こちらを参考にしました)
帰無仮説：２つのカテゴリー変数間には連関がない(独立である）
有意性検定のα値：5％

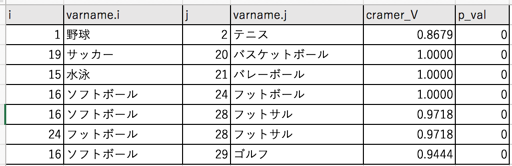
##アウトプットイメージ
i列とj列は、入力データフレームの変数の連番です。

##インプットデータのイメージ
1)カテゴリーデータのデータセット
このようなダミー変数（０と１からなる）のデータか

var_1,var_2,var_3
1, 1, 0,
0, 1, 1,
0, 0, 1,
・・・

このようなカテゴリーデータを想定しています。
（数値にみえますが、カテゴリーと思って下さい）
var_1,var_2,var_3
1, 5, 3,
2, 1, 2,
1, 5, 2,
・・・

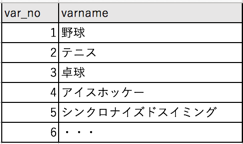
2)変数連番と変数名のデータセット

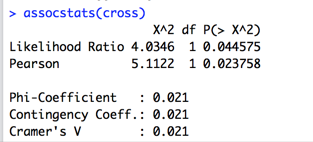
##assocstats関数の結果

• Likelihood Ratio(尤度比統計量）
• Pearson (χ2値)
• Phi-Coefficient (ファイ係数)
• Contingency Coeff (ピアソンの一致性係数)
• Cramer'sV (クラメールのV係数)

が出力されます。

クラメールVが5％水準で有意（帰無仮説を棄却できる）かどうかは、ピアソンのχ2値のp値を使って判定できます(根拠とした教科書 p.785)。

##Rのサンプルコード

cramer_v.R

#データを読み込む
df<read.table("testdata.dat",header=T)


#変数ラベルの読み込み
var_list<-read.table("var_list",header=T)
head(cat_list)

#vcdを読み込みます。
library(vcd)

#全ての変数ペアについてクロス表を作成し、クラメールVを求めます
#変数の数
n<-ncol(df)
#--計算する変数ペアの数
nn<-0
for(i in 1:(n-1)){
  nn<-nn+(n-i)
}

#アウトプット用のマトリクス
output<-matrix(0,nrow=nn,ncol=4)
k<-0

for(i in 1: (n-1)){
  for(j in (i+1):n){
    #クロス表
    cross<-xtabs(~df[,i]+df[,j],data=df)
    #assocstats関数より、クロス表の分析統計量をresに格納する
    res<-assocstats(cross)
    #chisq_testsオブジェクトの出力のうちピアソンのχ2値のp値（P(>X^2)のセルがp値
    p_val<- res$chisq_tests[2,3]
    #cramerオブジェクトが、クラメールV係数
    cramer_v<-res$cramer
    #クラメールVが0.3以上、かつp値が5％以下の場合のみ保持する
    if(cramer_v >=0.3 && p_val <=0.05){
      k<-k+1
      output[k,1]<-i
      output[k,2]<-j
      output[k,3]<-cramer_v
      output[k,4]<-p_val
    }
  }
}
#変数名をつける。
colnames(output)<-c("i","j","cramer_V","p_val")

head(output)

#余計な行を削除する
output<-output[1:k,]

#変数ペアの１こめについて、変数ラベルを結合する.
output.2<-merge(output,var_list,by.x="i",by.y="var_no",all.x=TRUE)

#変数番号の後に、変数ラベルにする。
output.2<-output.2[c("i","varname","j","cramer_V","p_val")]

#varnameの変数名を変える（あとに同じ名前のフィールドをさらに結合するため）
colnames(output.2)<-c("i","varname.i","j","cramer_V","p_val")

#変数ペアの２こめ(j)について、変数ラベルを結合する。
output.2<-merge(output.2,var_list,by.x="j",by.y="var_no",all.x=TRUE)

#変数番号ｊの後に変数ラベルという順番に入れ替える。
output.2<-output.2[,c("i","varname.i","j","varname","cramer_V","p_val")]

#ｊの変数ラベルをvarname.jに変更する。
colnames(output.2)<-c("i","varname.i","j","varname.j","cramer_V","p_val")

#macのExcelで開くことを想定した出力
write.table(output.2,"クラメールV有意なペア.txt",sep="\t",fileEncoding = "CP932",row.names=F)

##クラメールV係数の利点

• ０〜１の範囲をとり、１に近いほど「２つの変数に連関の度合いが強い」と判断できるため、直感的に分かりやすい。
• クラメールVは、χ2値と異なりサンプルサイズによる影響を受けない。

##ファイ係数とクラメールV係数との使い分け
2×２クロス表　：ファイ係数
r×ｃクロス表：　クラメールV

2×2クロス表のクラメールVは、ファイ係数と同じ。
ファイ係数もクラメールVもカイ二乗値を元に計算できる（式はこちら）

##ファイ係数と相関係数の使い分け
量的な変数の線形の関係の度合い：相関係数
ダミー変数の相関係数：ファイ係数

##参考）実行時間
およそ1,000変数で１時間10分程度

実行環境

• CPU Intel Core i5 2.7GHz
• メモリ 16GB
• OS OS X El Capitan
• R version 3.2.2 (2015-08-14)
• Platform: x86_64-apple-darwin13.4.0 (64-bit)
• Running under: OS X 10.11.3 (El Capitan)