※本記事は数理最適化Advent Calender2020 の 10 日目の記事です。9 日目の記事は、Exception in thread "main" java.lang.NullPointerException
はじめに
Python のデータ操作ライブラリである pandas は、数理最適化モデルの変数を保持するデータ構造として優秀です。数理最適化を業務に利用する際は、変数の添字が整数ではなく [顧客1, 顧客2, ...] のような文字列になることも多いですが、pandas では、そのような添字を index や columns として自然に表現できます。また、Series や DataFrame に用意されている集計関数の一部(sum や dot 等)は、最適化の変数にもそのまま適用可能です。
pandas を使ったモデルの表現方法は、一通りではありませんが、本記事では、ネット上の色々な方の実装を参考にしつつ、自分でも実際にモデリングを行ってみて、現時点で私が最も「すっきり」書けると思った記述方法をご紹介したいと思います。
なお、本記事における最適化モデルは、PuLP や Google OR-Tools 等の、いわゆるモデリングライブラリを使用する前提で記述しています。また、「すっきり」書くことを主眼に置いた記述方法であり、他の方法には速度面で劣っている可能性があります(この点については最後にも触れます)。あくまで、実装の一つの選択肢として受け取っていただけると嬉しいです。また、「こうすると良いのでは」等のコメントも募集しています!
題材: 輸送最適化
本記事では、モデリングの題材として簡単な輸送最適化を使用します。具体的には、以下のように、複数の工場から複数の顧客に対し、顧客の需要を満たすよう商品を輸送することを考えます。
期間は一年間とし、月ごとに各顧客の需要が与えられるものとします。簡単のため、各工場に在庫は存在せず、必要に応じて即座に任意量の生産が可能とします。輸送にかかる時間も考慮しません。
この上で、輸送コストと生産コストの和が少なくなるように輸送経路を決定します。
上記の輸送最適化を数式として定式化したものが、以下になります。
$$
\min_{transport} \left(\text{total_transport_cost} + \text{total_produce_cost} \right),
$$
$$
\begin{aligned}
\text{total_transport_cost} &= \sum_{\substack{f\in\mathrm{FACTORIES}\\ c\in\mathrm{CUSTOMERS} \\ t\in\mathrm{PERIODS}}} \text{transport_uc}_{f, c} \times transport_{f, c, t}, \
\text{total_produce_cost} &= \sum_{\substack{f\in\mathrm{FACTORIES}\\ t\in\mathrm{PERIODS}}} \text{produce_uc}_f \times produce_{f, t}, \
produce_{f, t} &= \sum_{c\in \mathrm{CUSTOMERS}} transport_{f, c, t}, \
\text{s.t.} ~~\text{demand}_{c, t} &= \sum_{f\in \mathrm{FACTORIES}} transport_{f, c, t}.
\end{aligned}
$$
ここで、上式で出てくる記号の定義は以下の通りです。
| 名前 | 説明 |
|---|---|
| PERIODS | 月の集合 |
| FACTORIES | 工場の集合 |
| CUSTOMERS | 顧客の集合 |
| produce_uc | 工場ごとの生産単価 |
| transport_uc | 工場、顧客ごとの輸送単価 |
| demand | 顧客、月ごとの需要量 |
| produce | 工場、月ごとの生産量 |
| transport | 工場、顧客、月ごとの輸送量 |
pandas を用いたモデル化
上記の輸送最適化問題を、pandas を用いて実際にモデル化してみます。
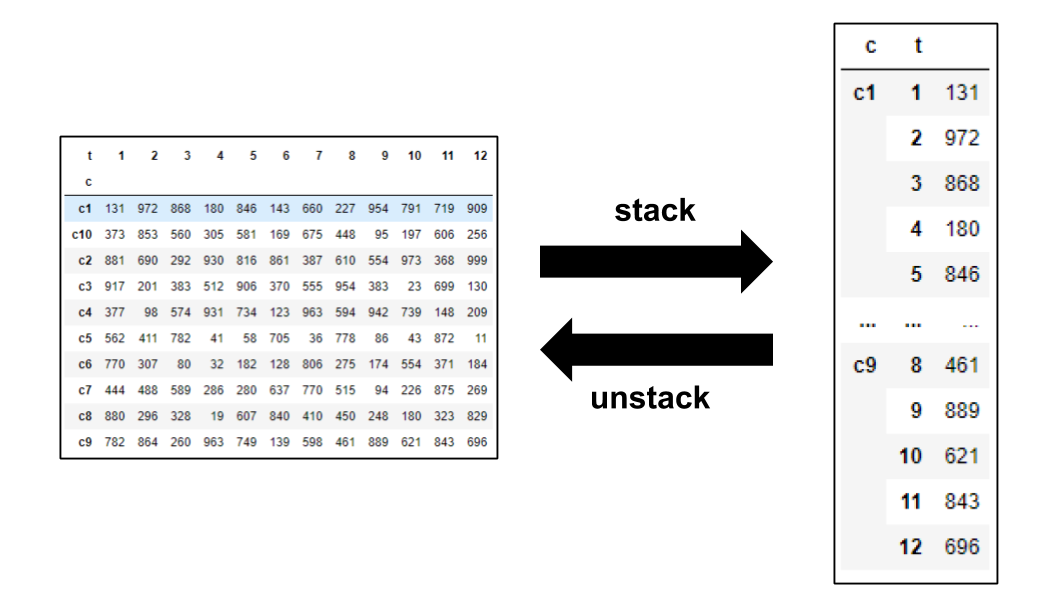
今回紹介する方法を一言でまとめると、「定数・変数は全て Series で宣言し、必要に応じて stack/unstack する」というものになります。ここで、stack は DataFrame の columns を index 側に移動する処理であり、unstack はその逆です。
集合
集合は、以下のようにソート済みリストとして定義します。
PERIODS = sorted([1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12])
FACTORIES = sorted(["f1", "f2", "f3", "f4", "f5"])
CUSTOMERS = sorted(["c1", "c2", "c3", "c4", "c5", "c6", "c7", "c8", "c9", "c10"])
pandas の stack/unstack/pivot が勝手にソートを行ってしまう関係で、何もしないと添字の順番が途中で変わってしまう可能性があるため、上記のソートは必要な処理になっています。
また、上記の集合を組み合わせた複合的な添字についても、以下で定義しておきます。
idx_fc = pd.MultiIndex.from_product((FACTORIES, CUSTOMERS), names=("f", "c"))
idx_ct = pd.MultiIndex.from_product((CUSTOMERS, PERIODS), names=("c", "t"))
idx_fct = pd.MultiIndex.from_product((FACTORIES, CUSTOMERS, PERIODS), names=("f", "c", "t"))
names を指定して pd.MultiIndex を明示的に作成しているのがミソで、添字の各レベルに名付けておくことで、stack/unstack による操作がしやすくなります。
定数
上記の集合を添字とするような最適化の前提データを、以下のように定義します。数字は適当に乱数で生成しました。
produce_uc = pd.Series(np.random.random(5), index=FACTORIES) # 生産単価
transport_uc = pd.Series(np.random.random(5 * 10), index=idx_fc) # 輸送単価
demand = pd.Series(np.random.randint(0, 1000, 10 * 12), index=idx_ct) # 需要
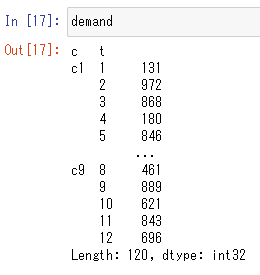
なお、pd.MultiIndex を使用すると、次のように階層的な添字を持つ Series になります。
変数
今回最適化の対象とするのは輸送量のみなので、工場・顧客・月の組み合わせごとに、輸送量を定義します(生産量は輸送量から計算可能)。
# 輸送量
transport = pd.Series(pl.LpVariable.dicts("transport", idx_fct, lowBound=0), index=idx_fct)
目的関数
まず、輸送コストの計算を行います。
$$
\text{total_transport_cost} = \sum_{\substack{f\in\mathrm{FACTORIES}\\ c\in\mathrm{CUSTOMERS} \\ t\in\mathrm{PERIODS}}} \text{transport_uc}_{f, c} \times transport_{f, c, t}
$$
この式は、これまで定義した定数・変数を用いて、次のように表現できます。
total_transport_cost = pl.lpSum((transport_uc * transport.unstack(level=("f", "c"))).to_numpy())
pandas の Series と DataFrame の積を取る際は、Series の index と DataFrame の columns の添字を揃える必要があることに注意してください。
なお、pandas の sum 関数を使うこともできますが、次のように 10 倍近く時間がかかってしまいました。pandas を使用するメリットとして、「pandas の集計関数が使用できる」という点を挙げましたが、可能な場合はモデリングライブラリ付属の高速な集計関数を使った方がよさそうです。
続いて、次の生産コストを計算します。
$$
produce_{f, t} = \sum_{c\in \mathrm{CUSTOMERS}} transport_{f, c, t}, \
\text{total_produce_cost} = \sum_{\substack{f\in\mathrm{FACTORIES}\\ t\in\mathrm{PERIODS}}} \text{produce_uc}_f \times produce_{f, t}.
$$
1 行目で顧客について足し合わせて生産量の計算を行い、2 行目で生産単価と掛け合わせて合計しています。
produce = transport.sum(level=("f", "t")) # produce[f, t]
total_produce_cost = pl.lpSum((produce_uc * produce.unstack(level="f")).to_numpy())
ちなみに、pandas の行列積メソッドを使用した場合は、少しだけ遅くなってしまいました。やはり、なるべくライブラリ付属の集計関数を使用した方がよさそうです。
目的関数は、輸送コストと生産コストの和になります。
model = pl.LpProblem("Logistics", pl.LpMinimize)
model.setObjective(total_transport_cost + total_produce_cost)
制約式
最後に、「顧客の需要を満たすように輸送を行う」という制約をモデルに追加します。
sell = transport.sum(level=("c", "t")) # sell[c, t]
for (c, t) in idx_ct:
model.addConstraint(sell[c, t] == demand[c, t])
モデル全体
これまでの内容を簡単に整理してまとめると、以下のようになります。
import pulp as pl
import numpy as np
import pandas as pd
np.random.seed(0) # 再現性のために乱数シードを指定
# 集合
PERIODS = sorted([1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12])
FACTORIES = sorted(["f1", "f2", "f3", "f4", "f5"])
CUSTOMERS = sorted(["c1", "c2", "c3", "c4", "c5", "c6", "c7", "c8", "c9", "c10"])
idx_fc = pd.MultiIndex.from_product((FACTORIES, CUSTOMERS), names=("f", "c"))
idx_ct = pd.MultiIndex.from_product((CUSTOMERS, PERIODS), names=("c", "t"))
idx_fct = pd.MultiIndex.from_product((FACTORIES, CUSTOMERS, PERIODS), names=("f", "c", "t"))
# 定数
produce_uc = pd.Series(np.random.random(5), index=FACTORIES)
transport_uc = pd.Series(np.random.random(5 * 10), index=idx_fc)
demand = pd.Series(np.random.randint(0, 1000, 10 * 12), index=idx_ct)
# 変数(従属変数を含む)
transport = pd.Series(pl.LpVariable.dicts("transport", idx_fct, lowBound=0), index=idx_fct)
produce = transport.sum(level=("f", "t")) # produce[f, t]
sell = transport.sum(level=("c", "t")) # sell[c, t]
# 目的関数
total_transport_cost = pl.lpSum((transport_uc * transport.unstack(level=("f", "c"))).to_numpy())
total_produce_cost = pl.lpSum((produce_uc * produce.unstack(level="f")).to_numpy())
model = pl.LpProblem("Logistics", pl.LpMinimize)
model.setObjective(total_transport_cost + total_produce_cost)
# 制約式
for (c, t) in idx_ct:
model.addConstraint(sell[c, t] == demand[c, t])
model.solve()
print(pl.LpStatus[model.status])
上記を実行すると、'Optimal' と表示され、無事最適化を実行することができました。
最適化結果の確認
pandas を使用して変数を宣言しておくと、結果の確認も容易に行うことができます。
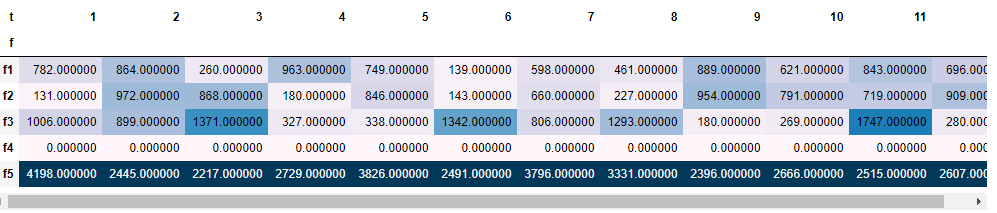
たとえば、最適化結果の生産量を、色分けして表形式で表示するコードは、以下のように書くことができます。
produce_value = produce.apply(lambda x: x.value()).unstack() # 変数の値を評価して DataFrame に変換。
produce_value.style.background_gradient() # 背景を色分け。
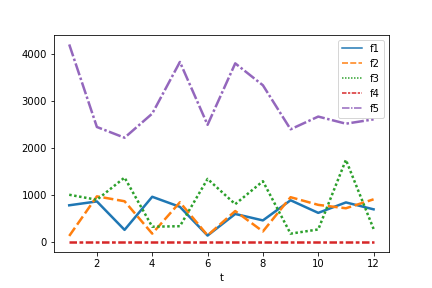
当然、seaborn 等の可視化ライブラリを使用することもできます。
import seaborn as sns
sns.lineplot(data=produce_value.T, linewidth=2.5)
他の実装方法との比較
というわけで、以上が「定数・変数は全て Series で宣言し、必要に応じて stack/unstack する」という実装方法の紹介でした。以降では、考えられる他の選択肢を挙げ、比較します。
まず、DataFrame ではなく Series を使用する理由ですが、「モデルの中でイテレートしたい添字が、目的関数や制約によって変わる可能性がある」というのが主な理由です。基本的に、DataFrame の columns 側がイテレートされる添字になるのですが、初めから DataFrame で宣言すると、別の添字の組み合わせに関する処理が書きづらくなります(一度 stack してから unstack する必要があります)。
加えて、プロダクションコードでは、モデルをクラス化し、データを引数として入力するのが典型的な実装だと思いますが、そのときにいちいち「どの定数が Series で、どの定数が DataFrame か」を意識するのは面倒です。それであれば、全て Series に統一し、必要な時に stack/unstack する方が良い、という判断をしています。
また、素直に dict で変数を宣言し、リスト内包表記を用いて計算する方法もあります。例えば、今回出てきた生産量 produce は、輸送量を dict で宣言すると、以下のように計算できます。
produce = {(f, t): sum(transport[f, c, t] for c in CUSTOMERS)
for f in FACTORIES for t in PERIODS}
これはこれで、内包表記に慣れていれば十分読めるものですが、Jupyter 上での表示や、可視化ライブラリとの連携性を考えると、pandas のクラスを用いる方が何かと便利だと思います。
おわりに
本記事では、pandas と PuLP を組み合わせて「すっきり」モデリングを行うための表現方法を紹介しました。
なお、簡潔に記述した結果、パフォーマンス面で損をしている可能性があり、この点は注意しなければいけないと感じています。具体的には、pandas の loc や stack/unstack を多用するため、添字の階層が深い&要素が多いときは、フィルターや stack/unstack に時間がかかることがあります。この辺りは、pandas の仕様を調査して、高速化を行う余地があるように思います。もし pandas の indexing や reshape 周りのパフォーマンスに詳しい方がいらっしゃれば、ぜひコメントで教えていただけると大変ありがたいです。
また、本記事と同じように、輸送最適化を pandas + PuLP の組み合わせで解いている記事として、@SaitoTsutomu さんのこちらの記事がありました。こちらの記事では、以下のように定数や変数を同じ DataFrame に格納する形でモデリングを行っているようです。
上記の筆者の方が作られた、pandas と PuLP を組み合わせて使うためのライブラリとして、ortoolpy というものがあります。こちらのライブラリは、基本的には上の記事の記法によるモデリングをサポートするためのもののようです。
というわけで、数理最適化アドベントカレンダー 10 日目の記事でした。こういった書き方の話というのは、「動けばよい」という観点では無駄ですし、行き過ぎるとただの過剰品質だなとも思うのですが、無理のない範囲で意識できれば、可読性や保守性に貢献できてみんなハッピ~と思っています。
長文を最後まで読んでいただいてありがとうございました。
よいお年を。