はじめに
数理計画法 (mathematical programming) とは、目的関数と呼ばれる目標値を、ある制約の下で最大化(最小化)する手法です。その中でも、線形計画法 (linear programming; LP) は、目的関数と制約式が変数に関する一次式($\sum_ia_ix_i + b$ という形の式)で表せるものを言います。線形計画法は、数理計画法の中でも単純なものの 1 つですが、それゆえにソルバーやモデリング用のライブラリが充実しており、利用しやすい環境が整っています。特に、企業においては、利益やコストといった金銭的な指標を目的関数として、生産量や輸送量といった制御可能な変数を最適化することが多いかと思います。
本記事では、数理最適化のモデリング技法についてまとめられた以下の書籍から、演習問題を 1 つ取り出して実際に定式化し、Python のモデリング言語である PuLP で実装して最適解を求めるところまでやっていきたいと思います。
Model Building in Mathematical Programming
https://www.amazon.co.jp/dp/1118443330/
なお、この演習問題は TFUG の数理最適化グループで行っている輪読の宿題の一つです。TFUG のグループは誰でも参加可能ですので、興味がある方は Slack を覗いてみると良いかもしれません!
本記事は、以下のような構成になっています。始めにモデリングの仕方について簡単に説明した後、例題の問題設定を紹介し、モデリング、実装、検証を行っていきます。
- モデリングの流れ
- 問題設定
- モデリング
- コラム 1:モデリングの恣意性
- モデルの実装
- モデルの検証
- コラム 2:数理最適化モデルのテスト
- おわりに
途中でコラム的な節が挟まっており、読み飛ばしても問題ありませんが、個人的に面白いと感じているトピックについて書いているので、ぜひ読んでみてください。
モデリングの流れ
一般論として、何らかの計画を数理的にモデル化するには、以下の 2 つを定義する必要があります。
- 目的関数
- 制約式
工場の生産計画を例に考えてみましょう。まず、目的関数は、最適化したいコストや利益を表します。例えば、工場 A と工場 B で生産を行うとき、生産コストは次のように表すことができると仮定します。
$$
\text{生産コスト} = \sum_{i \in \{A, B\}} \text{生産単価}_i \times \text{生産量}_i.
$$
この場合、生産単価の高い工場の生産量を減らし、生産単価の低い工場の生産量を増やすことで、生産コストを低く抑えることができそうです。しかし、この式だけでは、実は本当に求めたい最適解を求めることはできません。なぜなら、「○○以上の量を生産しなければいけない」という制約がないため、純粋に生産コストを最小化しようとすると、全く生産を行わないのが最適解になってしまうからです。
そこで、次に制約式として、このような事態を避けるために変数に条件を課します。例えば、先ほど触れた「○○以上の量を生産しなければいけない」という制約は、次のように表せます。
$$
\sum_{i \in \{A, B\}} \text{生産量}_i \geq \text{需要量}.
$$
他にも、生産計画であれば、工場の生産能力に限度があり、生産量の上限が決まっていることが多いでしょう。こういった業務上の制約や決まりを、数式として表現したものが制約式です。
また、目的関数と制約式を定義するには、以下の情報が必要になります。
- 集合
- 最適化の対象となる要素の集まり。
- 例:工場、対象期間(月や日にち)等。
- パラメータ
- 目的関数や制約式の計算に使用する数値。
- 例:生産単価、生産量上限、需要量等。
- 変数
- 実際に最適化を行いたい数値。
- 例:生産量、輸送量等。
実際に自分で一からモデリングする場合は、個人的には、まず目的関数を定義するのを目指すのがよいと思います。目的関数を定義しようとすると、その過程で必要な情報を整理する必要があるので、集合やパラメータ、変数を決めることにも繋がります。その後、各変数に関して、必要な制約を洗い出し、1 つ 1 つ式として表現していけば完成です。
以降では、例題の問題設定を紹介し、実際にモデリングしていきます。
問題設定:Food manufacture 1
今回扱うのは、食品の生産計画です。具体的には、1 月から 6 月に渡り、毎月原料となる油を購入し、精製・混合することで、食品を作るそうです(マーガリンか何か……?)。この生産計画の中で、各月の各原料油の購入量や消費量を調整することで、最終的に利益を最大化することを目指します。
今回の問題で、目的関数や制約式を考えるには、以下の要素に関係するコストや制約を考える必要があります。
- 在庫
- 購入
- 精製
- 混合
- 販売
それぞれの状況について、詳しく説明していきます。
在庫
原料油の在庫は、新たに購入すると増加し、食品の生産に消費すると減少します。
各原料油は、それぞれ $1000 [t]$ まで在庫として保持しておくことができます。ただし、1 か月あたり $5 [£/t]$ の保管コストがかかります。
また、どの原料油に関しても、在庫は $500 [t]$ で始まり、最終的に $500[t]$ 以上は残すものとします。
購入
上記の油を、1 月から 6 月にかけて、以下の単価で購入します。
| 月 | VEG 1 | VEG 2 | OIL 1 | OIL 2 | OIL 3 |
|---|---|---|---|---|---|
| Jan | 110 | 120 | 130 | 110 | 115 |
| Feb | 130 | 130 | 110 | 90 | 115 |
| Mar | 110 | 140 | 130 | 100 | 95 |
| Apr | 120 | 110 | 120 | 120 | 125 |
| May | 100 | 120 | 150 | 110 | 105 |
| Jun | 90 | 100 | 140 | 80 | 135 |
購入できる量には、特に制約はありません。
精製
購入した量と元々在庫にあった量のうち、ある量を精製プロセスにかけます。精製する過程では、特にロス等はないものとし、精製にかかるコストも無視できるものとします。
原料油には、植物性と非植物性という 2 つの種類があり、精製プロセスは、油の種類ごとに異なる精製ラインで行われるそうです。精製量の上限は以下のように設定されています。
| 種類 | 精製量上限[t/月] |
|---|---|
| 植物性 | 200 |
| 非植物性 | 250 |
また、原料油の種類は以下のようになっています。
| 名前 | 種類 |
|---|---|
| VEG 1 | 植物性 |
| VEG 2 | 植物性 |
| OIL 1 | 非植物性 |
| OIL 2 | 非植物性 |
| OIL 3 | 非植物性 |
混合
精製した油をすべて混合することで、その月に出荷する食品が完成します。ここでも特にロスは発生しないため、混ぜ合わせた原料油の重量の総和が食品の生産量になります。
また、それぞれの原料油は、下表に示す硬度を持っています。生産される食品の硬度は、原料油の消費量に応じた平均になり、食品の硬度は $3$ から $6$ の間に納まらないといけないそうです。
| 名前 | 硬度 |
|---|---|
| VEG1 | 8.8 |
| VEG2 | 6.1 |
| OIL1 | 2.0 |
| OIL2 | 4.2 |
| OIL3 | 5.0 |
販売
生産した食品は、その月のうちに必ず売り切ることが可能だそうです。つまり、生産量がそのまま販売量になります。販売単価は、月によらず $150 [£/t]$ で一定とします。
モデリング:Food manufacture 1
これから、先ほど説明した問題設定を、実際にモデル化していきます。なお、先ほど「目的関数を定義する中で集合やパラメータを決めていくのがよい」と書きましたが、説明には集合、パラメータ、変数を先に書いた方が楽なので、そうしています。
集合
数理最適化モデルにおいて、パラメータや変数の添字になるのが集合です。
今回の問題では、以下の 4 つの集合を考えることにします。
原料油
$$
\text{OILS} = \{\text{VEG1}, \text{VEG2}, \text{OIL1}, \text{OIL2}, \text{OIL3}\}.
$$
対象期間(月)
$$
\text{TIME_IDX} = \{1, \ldots, 6 \}.
$$
精製ライン
$$
\text{REF_LINES} = \{\text{VEG}, \text{NONVEG} \}.
$$
精製対象
精製ラインごとに定義するので、全体としては集合の集合(集合族)になります。
$$
\text{USED_OILS} = \{\text{USED_OILS}_{VEG}, \text{USED_OILS}_{NONVEG}\}.
$$
各精製ラインの中身の集合は、
$$
\begin{aligned}
\text{USED_OILS}_{VEG} &= \{\text{VEG1}, \text{VEG2}, \text{VEG3}\}, \
\text{USED_OILS}_{NONVEG} &= \{\text{OIL1}, \text{OIL2}\}.
\end{aligned}
$$
ここでは天下り的に与えていますが、集合の定義の仕方は一意ではないことに注意してください。集合の定義の仕方によっては、モデルの汎用性が下がってしまうこともあります。これについては、制約式の節で詳しく触れます。
パラメータ
次に、目的関数や制約式の計算に使用するパラメータを定義していきます。
| 名前 | 添字 | 値域 | 説明 |
|---|---|---|---|
| $\text{buy_uc}$ | $\text{OILS}$ $\text{TIME_IDX}$ |
$[0, +\infty)$ | 原料油の購入単価。 |
| $\text{stock_uc}$ | - | $[0, +\infty)$ | 原料油の保管単価。 |
| $\text{sell_uc}$ | - | $[0, +\infty)$ | 食品の販売単価。 |
| $\text{stock_init}$ | $\text{OILS}$ | $[0, +\infty)$ | 原料油の初期在庫。 |
| $\text{stock_final_lb}$ | $\text{OILS}$ | $[0, +\infty)$ | 原料油の最終的な在庫量の下限。 |
| $\text{stock_ub}$ | - | $[0, +\infty)$ | 原料油の在庫量上限。 |
| $\text{hardness}$ | $\text{OILS}$ | $[0, +\infty)$ | 原料油の硬度。 |
| $\text{ref_ub}$ | $\text{REF_LINES}$ | $[0, +\infty)$ | 精製量の上限。 |
uc は単価を意味する unit cost の略、lb/ub はそれぞれ lower/upper bound の略で、上下限という意味です。
変数
同様に、最適化の対象となる変数を定義します。変数名には名詞を使うのが望ましいですが、長すぎると式が見づらいので、一部動詞にしています。
| 名前 | 添字 | 値域 | 説明 |
|---|---|---|---|
| $\text{buy}$ | $\text{OILS}$ $\text{TIME_IDX}$ |
$[0, +\infty)$ | 原料油の購入量。 |
| $\text{use}$ | $\text{OILS}$ $\text{TIME_IDX}$ |
$[0, +\infty)$ | 原料油の使用量。 |
| $\text{produce}$ | $\text{TIME_IDX}$ | $[0, +\infty)$ | 食品の生産量。 |
| $\text{opening_stock}$ | $\text{OILS}$ $\text{TIME_IDX}$ |
$[0, \text{stock_ub}]$ | 原料油の月初在庫。 |
| $\text{closing_stock}$ | $\text{OILS}$ $\text{TIME_IDX}$ |
$[0, \text{stock_ub}]$ | 原料油の月末在庫。 |
在庫については、$\text{opening_stock}$ と $\text{closing_stock}$ のうち片方だけ宣言すれば十分な場合も多いです。この辺りは個人の好みもあります。
目的関数
必要な情報が出揃ったので、目的関数を定義していきます。今回は、期間全体の利益を最大化したいのでした。
$$
\text{maximize} ~~\text{total_profit}.
$$
ここで、利益は売上と各種コストを用いて、次のように計算できます(なお、会計用語としての「利益」とは厳密には一致しません。設備投資などの固定費は最適化の対象外なので今回無視しています)。
$$
\text{total_profit} = \text{total_sales} - \text{total_buy_cost} - \text{total_stock_cost}
$$
売上と各種コストは、関係する食品や原料油の量と単価をかけ合わせることで計算できます。
$$
\begin{align}
\text{total_sales} &= \text{sell_uc} \times \sum_{t\in \text{TIME_IDX}} \text{produce}_t, \
\text{total_buy_cost} &= \sum_{oil\in \text{OILS}, t\in \text{TIME_IDX}} \text{buy_uc}_{oil, t} \times \text{buy}_{oil, t}, \
\text{total_stock_cost} &= \text{stock_uc} \times \sum_{oil\in \text{OILS}, t\in \text{TIME_IDX}} \text{closing_stock}_{oil, t}.
\end{align}
$$
制約条件
次に、制約式を書き下していきます。
変数の単純な上下限については、「変数」の節で値域として書いています。
初期在庫、最終在庫
1 月の月初在庫は、初期在庫に一致します。
$$
{}^\forall oil\in \text{OILS}, ~~\text{opening_stock}_{oil, 1} = \text{stock_init}_{oil}.
$$
6 月の月末在庫は、最終在庫下限以上になるものとします。
$$
{}^\forall oil\in \text{OILS}, ~~\text{closing_stock}_{oil, 6} \geq \text{stock_final_lb}_{oil}.
$$
在庫バランス
2 月以降の月初在庫は、前の月の月末在庫に一致します。
$$
{}^\forall t\in {2,\ldots,6}, ~~{}^\forall oil\in \text{OILS}, ~~\text{opening_stock}_{oil, t} = \text{closing_stock}_{oil, t - 1}.
$$
月末在庫は、その月の月初在庫に購入量を加え、消費量を引いた量になります。
$$
{}^\forall t\in \text{TIME_IDX}, ~~{}^\forall oil\in \text{OILS}, ~~\text{closing_stock}_{oil, t} = \text{opening_stock}_{oil, t} + \text{buy}_{oil, t} - \text{use}_{oil, t}.
$$
生産量バランス
各月の生産量は、原料油の消費量の総和に一致します。
$$
{}^\forall t\in \text{TIME_IDX}, ~~\text{produce}_t = \sum_{oil \in \text{OILS}} \text{use}_{oil, t}.
$$
硬度
「生産される食品の硬度は、原料油の消費量に応じた平均になり、食品の硬度は $3$ から $6$ の間に納まらないといけない」という部分ですが、少し複雑です。問題文を素朴に式で表すと、次のようになりますが、変数に関する一次式になっていません。
$$
3 \leq \frac{\sum_{oil\in \text{OILS}} \text{hardness}_{oil} \times \text{use}_{oil, t}}{\text{produce}_t} \leq 6.
$$
しかし、分母を払うことで、一次式に変換することができます。
$$
3 \times \text{produce}_t \leq \sum_{oil\in \text{OILS}} \text{hardness}_{oil} \times \text{use}_{oil, t} \leq 6 \times \text{produce}_t.
$$
さらに、元々の式では生産量が $0$ の場合の挙動が怪しいですが、変換後の式であれば、消費量・生産量共に $0$ になるため、制約を満たすことが分かります。今回の問題設定では、生産を行わないということも考えられるので、問題ありません。
精製量上限
今回の生産計画では、精製ラインごとに精製量の上限がありました。式で表現すると、次のように書けます。
$$
{}^\forall line\in \text{REF_LINES}, ~~{}^\forall t\in \text{TIME_IDX}, \sum_{oil\in \text{USED_OILS}_{line}} \text{use}_{oil, t} \leq \text{ref_ub}_{line}.
$$
少し分かりづらいかもしれませんが、各精製ラインに関して、対象となる原料油の消費量の和が、ある上限以下となるような制約をかけています。
コラム 1:モデリングの恣意性
なお、精製ラインに関する情報は、別の表現をすることもできます。例えば、$\text{USED_OILS}$ の代わりに、各原料油の精製ラインを意味するパラメータ $\text{ref_line}$ を次のように定義してみます。
| 添字 | 値 |
|---|---|
| VEG1 | VEG |
| VEG1 | VEG |
| OIL1 | NONVEG |
| OIL2 | NONVEG |
| OIL3 | NONVEG |
これは、問題文に出てきた原料油の種類の表ほぼそのままですから、こちらを使う方が自然かもしれません。このパラメータを使えば、精製量上限の制約は、次のように表現できます。
$$
{}^\forall line\in \text{REF_LINES}, ~~{}^\forall t\in \text{TIME_IDX}, \sum_{\substack{oil\in \text{OILS} ~\text{s.t.} \\ \text{ref_line}_{oil} = line}} \text{use}_{oil, t} \leq \text{ref_ub}_{line}.
$$
やっていることは先ほどと同じで、精製対象となる原料油の消費量を足し合わせ、上限で抑えているだけです。こちらのモデルでも、今回のデータであれば、同一の結果を得ることができます。
しかし、どちらの方が望ましいかは、一考の余地があります。
試しに、$\text{VEG1}$ と $\text{VEG2}$ の精製を行う $\text{VEGNEW}$ というラインが追加されるケースを考えてみましょう。既存の原料油の一部しか精製できないラインが作られるというのは、まぁありそうなことです。元のモデルであれば、次のように表現できます。
$$
\begin{aligned}
\text{USED_OILS} &= \{\text{USED_OILS}_{VEG}, \text{USED_OILS}_{VEGNEW}, \text{USED_OILS}_{NONVEG}\},\
\text{USED_OILS}_{VEG} &= \{\text{VEG1}, \text{VEG2}, \text{VEG3}\}, \
\text{USED_OILS}_{VEGNEW} &= \{\text{VEG1}, \text{VEG2}\}, \
\text{USED_OILS}_{NONVEG} &= \{\text{OIL1}, \text{OIL2}\}.
\end{aligned}
$$
しかし、$\text{ref_line}$ を使う定式化をしていたら、どうでしょうか? 先ほどの表を見てわかるように、このパラメータは 1 つの原料油について、精製ラインが必ず 1 つに定まることを前提としています。したがって、$\text{VEG1}$ が $\text{VEG}$ にも $\text{VEGNEW}$ にも属する状況は、モデルで表すことができません。
このように、集合とパラメータの定義の仕方 1 つとっても、汎用性の持たせ方には幅があります。問題についての理解が浅いと、間違った方向に汎用性を持たせてしまい(あるいは持たせ損ない)、後でモデルを修正するのが大変になる、なんてこともあります(cf. 早すぎる抽象化 (premature abstraction))。
あらかじめ全ての変更を予見できるわけではありませんし、法改正などで仮定そのものが変わってしまうこともありますが、こういった何気ない集合の定義の仕方に、恣意的な仮定が紛れ込んでいることを自覚するのが重要だと思います。また、実際にモデリングするときには、ユーザー(ドメインエキスパート)の力を借りて、業務への理解を深めることも欠かせません。
モデルの実装:Food manufacture 1
上記のモデルを Python + PuLP で実装していきます。PuLP では、集合やパラメータは Python の任意のデータ構造を使用できるため、使いやすいものを使えば十分です。以降では、変数の宣言、目的関数の定義、および制約式の定義について紹介します。
変数の宣言
PuLP の変数は、次のように宣言します。
# 名前 添字 下限 上限 種類(連続 or 整数)
buy = LpVariable.dicts("buy", (OILS, TIME_IDX), lowBound=0, upBound=None, cat='Continuous')
ちなみに、ドキュメントには載っていないのですが、行列のような形で宣言することもできるようです。
buy = LpVariable.matrix("buy", (OILS, TIME_IDX), lowBound=0, upBound=None, cat='Continuous')
目的関数の設定
まず、定義した変数やパラメータを用いて、目的関数を表現します。
# 目的関数の計算
total_sales = lpSum(produce[t] * sell_uc for t in TIME_IDX)
total_buy_cost = lpSum(buy[oil][t] * buy_uc[oil][t] for t in TIME_IDX for oil in OILS)
total_stock_cost = lpSum(closing_stock[oil][t] * stock_uc for t in TIME_IDX for oil in OILS)
total_cost = total_buy_cost + total_stock_cost
total_profit = total_sales - total_cost # 目的関数
次に、線形計画問題 LpProblem を定義し、目的関数を足し込むことで設定できます。
# モデルの定義と目的関数の設定
model = LpProblem("Food manufacture 1", LpMaximize)
model += total_profit
次のように、メソッドを使って目的関数を設定することもできます。
model.setObjective(total_profit)
目的関数を複数宣言した場合、最後のものだけが使われます。
制約式の設定
制約式も、目的関数と同じように、model に足し込むことで宣言可能です。
# 生産量バランス
for t in TIME_IDX:
model += produce[t] == lpSum(use[oil][t] for oil in OILS)
目的関数と書き方が同じですが、クラス名からうまく判別しているようです。メソッドで定義することも可能です。
model.addConstraint(produce[t] == lpSum(use[oil][t] for oil in OILS))
なお、これまで省略していましたが、目的関数にも制約式にも、個別に名前を付けることができます。
model += produce[t] == lpSum(use[oil][t] for oil in OILS), "Production balance"
コード全体
今回実装したモデルのコード全体は以下にまとめます。
from pulp import LpProblem, LpMaximize, LpVariable, lpSum
# 集合の定義
TIME_IDX = [1, 2, 3, 4, 5, 6]
OILS = ['VEG1', 'VEG2', 'OIL1', 'OIL2', 'OIL3']
REF_LINES = ['VEG', 'NONVEG']
USED_OILS = {
'VEG': ['VEG1', 'VEG2'],
'NONVEG': ['OIL1', 'OIL2', 'OIL3']
}
# パラメータの設定
sell_uc = 150
stock_uc = 5
stock_ub = 1000
stock_init = 500
stock_final_lb = 500
prod_ub = {'VEG': 200, 'NONVEG': 250}
hardness_lb = 3
hardness_ub = 6
hardness = {'VEG1': 8.8, 'VEG2': 6.1, 'OIL1': 2.0, 'OIL2': 4.2, 'OIL3': 5.0}
buy_uc = {
'VEG1': {1: 110, 2: 130, 3: 110, 4: 120, 5: 100, 6: 90},
'VEG2': {1: 120, 2: 130, 3: 140, 4: 110, 5: 120, 6: 100},
'OIL1': {1: 130, 2: 110, 3: 130, 4: 120, 5: 150, 6: 140},
'OIL2': {1: 110, 2: 90, 3: 100, 4: 120, 5: 110, 6: 80},
'OIL3': {1: 115, 2: 115, 3: 95, 4: 125, 5: 105, 6: 135}
}
# 変数の定義
buy = LpVariable.dicts("buy", (OILS, TIME_IDX), lowBound=0)
use = LpVariable.dicts("use", (OILS, TIME_IDX), lowBound=0)
produce = LpVariable.dicts("produce", TIME_IDX, lowBound=0)
opening_stock = LpVariable.dicts("opening_stock", (OILS, TIME_IDX), lowBound=0, upBound=stock_ub)
closing_stock = LpVariable.dicts("closing_stock", (OILS, TIME_IDX), lowBound=0, upBound=stock_ub)
# 目的関数の計算
total_sales = lpSum(produce[t] * sell_uc for t in TIME_IDX)
total_buy_cost = lpSum(buy[oil][t] * buy_uc[oil][t] for t in TIME_IDX for oil in OILS)
total_stock_cost = lpSum(closing_stock[oil][t] * stock_uc for t in TIME_IDX for oil in OILS)
total_cost = total_buy_cost + total_stock_cost
total_profit = total_sales - total_cost
# モデルの定義と目的関数の設定
model = LpProblem("Food manufacture 1", LpMaximize)
model += total_profit
# 制約式
# 初期在庫、最終在庫
for oil in OILS:
model += opening_stock[oil][TIME_IDX[0]] == stock_init
model += closing_stock[oil][TIME_IDX[-1]] >= stock_final_lb
# 各月に関して
for t in TIME_IDX:
# 在庫バランス
for oil in OILS:
if t != TIME_IDX[0]:
model += opening_stock[oil][t] == closing_stock[oil][t - 1]
model += closing_stock[oil][t] == opening_stock[oil][t] + buy[oil][t] - use[oil][t]
# 販売量バランス
model += produce[t] == lpSum(use[oil][t] for oil in OILS)
# 硬度
total_hardness = lpSum(hardness[oil] * use[oil][t] for oil in OILS)
model += total_hardness <= hardness_ub * produce[t]
model += total_hardness >= hardness_lb * produce[t]
# 精製量上限
for line in REF_LINES:
total_prod_amount = lpSum(use[oil][t] for oil in USED_OILS[line])
model += total_prod_amount <= prod_ub[line]
model.solve()
print(model.objective.value()) # 結果: 107842.59264500001
上記のコードを実行すると、目的関数の値として 107842.59264500001 という値が得られます。これは元々のテキストに書いてあるのと同じため、最適解が求まっていると考えて良さそうです。
モデルの検証:Food manufacture 1
前節で、テキストと同じ最適値が求まりました。しかし、実際に数理最適化を仕事で使うときは、最適値も最適解も分からないことが多く、今回のように「答え合わせ」できることは稀です。そこで、モデルを定性的に分析することで、結果の妥当性を検証します。
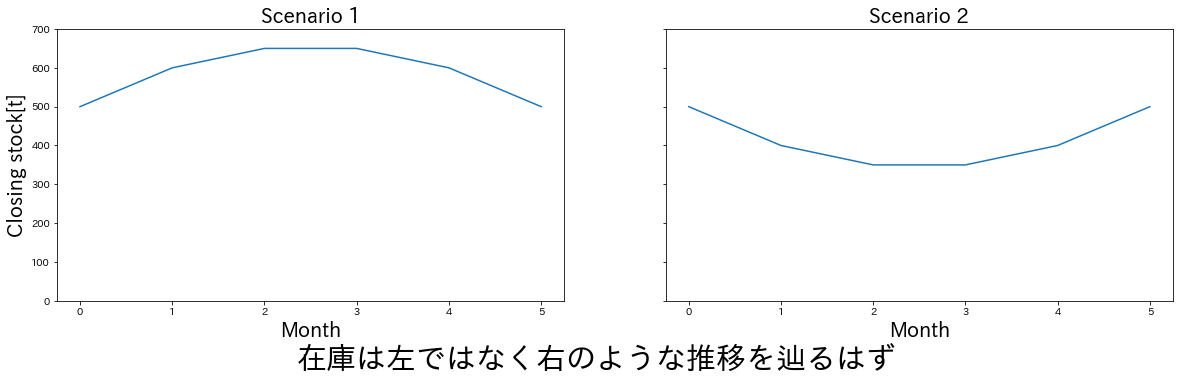
ここでの定性的な分析とは、モデルの定義から、最適解の取るべき値について予想を立て、実際の計算結果と比較することです。例えば、今回は最初と最後の在庫(の下限)が固定されており、毎月在庫量に応じたコストがかかるため、「まずは在庫を消費していき、途中から在庫を回復させていく方が利益が高くなるだろう」という予想が立てられます。
では、実際に最適解を表示して、この仮説を確かめてみましょう。
期末在庫の最適解は、次のように取得することができます。
closing_stock_value = {oil: {t: closing_stock[oil][t].value() for t in TIME_IDX} for oil in OILS}
以下のコードで、プロットしてみます。
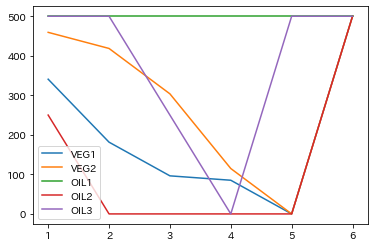
df = pd.DataFrame(closing_stock_value, index=TIME_IDX, columns=OILS)
df.plot()
全く使用していない OIL1 以外、全て初期在庫から 1 度落ちてから回復しており、最適化結果がそれなりに妥当そうだということが確認できました。
ここでは 1 つの仮説だけを検証しましたが、実際にはこのような reasonable な仮定をできるだけ多く立て、最適化結果を検証します。そして、もし最適解が全ての仮説通りの結果になっていたら、どうやら正しく実装できていそうだ、ということが分かります。逆に、最適解が仮説を満たしていなかったら、モデルの実装か、仮説のどちらかが間違っていることになります。これはこれで、モデルそのものを修正したり、モデルへの理解を深めるきっかけになり、非常に有用です。
コラム 2:数理最適化モデルのテスト
ところで、先ほど書いた検証の仕方に違和感を覚えた方もいるのではないでしょうか。ソフトウェアエンジニアなら、「制約が一つ一つ与えられているなら、それぞれについて単体テストを書けばよいのでは?」と思うかもしれません。それはその通りで、書ける状況なら書くべきです。
しかし、数理最適化モデルは、密結合な制約の巨大な集合であり、制約レベルの単体テストは多くの場合困難です。先ほどの制約式も、一見別々に見えて、実はモデルの中でお互いに依存しあっています。例えば、精製量上限の値を小さくしたら、硬度制約を満たせなくなる、ということが平気で起こります。もちろん、モデル自体を 1 つの巨大な関数と見立ててテストすることは可能ですが、同値クラスや境界値などを知ることは難しく、結局「発見的に仮説を立てて検証する」というところに戻ってきます(自動化はできますが)。
実際、オープンソースの数理最適化ソルバーのテストコードを見ても、挙動がわかりやすい toy problem をいくつか解くだけで済ましており、あまり厳密なテストはできていないように見えます(モデルのテストとソルバーのテストでは勝手が違うかもしれませんが)。
数理最適化のテストに関する研究や文献も探しましたが、私が調べた限りでは、それらしきものは見つかりませんでした。見逃しているだけの可能性もありますので、もし「こうすると良いよ」等の意見がありましたら、コメントいただけると幸いです。
一応、このあたりのテストの難しさは、MLSE のコミュニティが取り組んでいる、機械学習モデルのテストの問題にも近い気がするので、こちらのコミュニティの動向を追った方が良いかもしれません。
Challenges for machine learning systems toward continuous improvement
https://www.slideshare.net/chezou/challenges-for-machine-learning-systems-toward-continuous-improvement
ところで、どうでもいい話題ですが、以前、数理最適化を使っているっぽい以下の記事がプチ炎上して、「テストしろよ」みたいなコメントをされているのをみて、なんとも言えない気分になりました(関係者ではありませんが……)。
「AIで数秒」のはずが…保育所選考、連休返上で作業 さいたま市 - 毎日新聞
https://mainichi.jp/articles/20200204/k00/00m/040/176000c
ここまで書いたような方法で頑張って検証しても、予期していないデータでモデルが unbounded になったり infeasible になったりすることがあるので、頭が痛いです。世知辛い![]()
おわりに
ということで、生産計画を線形計画法としてモデル化し、PuLP で実際に解いて、結果を検証するところまでやってみました。単純にモデリングの説明だけでなく、少ないなりの実務経験を踏まえた、モデリングに対する自分なりの考えも書いたつもりです。
これからモデリングの練習を始めるのであれば、このモデルを自分なりにいろいろ変えてみると良いかもしれません。例えば、購入量に月・油の種類ごとの上下限を設けたり、精製プロセスで 1% ロスするように設定してみたり、色々考えられると思います。
本当はシリーズものにして、演習問題全部解きたかったんですが、力尽きました![]()
解くだけならまだしも、記事にするとなると大変ですね。
というわけで、もしこの記事が良いなと思ったら、チャンネル登録といいねお願いします!(YouTuber 風)。