目次
★★★★☆ 8/22 ARC125 B問題
★★★☆☆ 8/21 ABC215 E問題
★☆☆☆☆ 8/14 ABC214 D問題
★☆☆☆☆ 8/8 ABC213 D問題
★★★☆☆ 7/28 典型90 058
★★★★★ 7/24 ABC211 C問題 MODでの割り忘れ
★★★★☆ 7/24 ABC211 D問題
★★☆☆☆ 7/18 ARC123 C問題
はじめに
このページでは、同じミスを繰り返さないよう(コンテスト中に)実際にやらかしたミスを記録しています
★:ミスの注意度
太文字:過去に複数回やらかしたミス
arc125_b
コンテスト中に考えていたこと
模範解法との比較のため、具体的に何をやってうまくいかなかったのかをまとめておく
x^{2}-y = z^{2} (1≦x,y≦N)
$x$ を $1≦x≦N$ で動かしたときに、それぞれの $x$ に対し $z_{{min}}$ と $z_{{max}}$ を求めようとした。$x$ を $1$ から $N$ まで順に単調増加させたとき $z_{{min}}$ と $z_{{max}}$ も $0≦z_{{min}},z_{{min}}≦N$ で単調増加するため、計算量は ${O}(N)$ であると推測していた。
( $z_{{min}}$:$x^{2}-N ≦ z^{2}$を満たす最小の $z$ / $z_{{max}}$:$x^{2}-1 ≧ z^{2}$を満たす最大の $z$ )
Answer\:=\sum_{x=1}^{N} ({z}_{max}-{z}_{min}+1)
しかしながら制約が $1≦N≦10^{12}$ なので、計算量が ${O}(N)$ であるこの手法では TLE してしまう
そこで、 $z_{{min}}$ と $z_{{max}}$ を $x$ から直接求めることを考えたが、 $z_{{max}} = x-1$ はすぐわかるのに対し、 $z_{{min}}$ はうまく求められそうにないことから断念した。
Z\:=\:{z}_{max}-{z}_{min}+1
また、 $Z$ を動かしそれぞれの $Z$ を取りうる $x$ の範囲を求めようと考えたが、これも上手く求められそうにないことから断念した。
模範解法
\begin{align}
&x^{2}-y = z^{2} (1≦x,y≦N) \\
⇔ &x^{2}-z^{2} = y \\
⇔ &(x+z)(x-z) = y \\
⇔ &pq = y (p = x+z,\:q = x-z) \\
\end{align}
以上より、次の3つの条件を満たす正の整数 $p,q$ の組の数を考えればよい
\begin{align}
&① pq ≦N \\
&② p>q (∵\:p-q=2z) \\
&③ p≡q\:\:(mod\:\:2) (∵\:x=\frac{p+q}{2},\:z=\frac{p-q}{2}) \\
\end{align}
この条件を元に、それぞれの $q$ に対し組となりうる $p$ の数を求めればよい
反省点
模範解法は与えられた式を変形(平方完成)し、$x$ や $y$ 、$z$ よりも小さい $q$ ( ${O}(N)$ ) について考えるものであったが、1番最初の式変形の部分をできなかった。
Atcoderを始めた当初は数学の問題の感覚で解いていたのでおそらくこの問題を通せたように思えるが、最近はあまりこのような数学的な問題に出くわさず、やれ二分探索だのDPだのAtcoderで覚えたばかりの解法のことばかり考えていたため、B問題に割ける時間が110分あったにもかかわらず、このような数学的考察を行わなかった。
また、途中でC問題に移り、特に解法がわかったわけでもないのにそちらの方で沼にはまりB
B問題をあまり考察出来ていなかった。
abc215_e
そもそも解法に限界があった
過去に受けたコンテストによってによって遷移に影響があるので、それまでに受けたコンテストごとに分類しDPする解法は浮かんだが、以下の要因で模範解答のようには解かず、結果通せなかった
①まさか本当にそんな解き方をするとは思わなかった(実際はbitDPと呼ばれる典型的なDPらしいので、今後習得する)
②SはAからJまでの英大文字という制約を見逃していた(本当は2^10通りでいいが、2^26通りに分類すると勘違いし、TLEすると考えた)
解法の問題点
例えばi番目のコンテストがABCの場合、そのコンテストを受けられるのは
①最後に受けたコンテストがABCである
②最後に受けたコンテストはABCでないが、今までABCを受けたことがない
③(今までコンテストを受けたことがない)
であり、②を求めるために各A_Cに対し、最後に受けたコンテストがA_Cで、今までABCを受けたことがない 回数を記録する必要があるが、(WAした解法のように)愚直にそのケースを求めようとすると、例えば
最後に受けたコンテストがAACで、今までABCを受けたことがない
最後に受けたコンテストがAACで、今までACCを受けたことがない
という事象は互いに背反ではないので、模範解答のようなやり方(bitDP)でないと結局求めることができない
(まあ初めて見るタイプの問題だったし、コンテスト中にord()という新たな収穫もあったのでヨシ!)
abc214_d
通せなかった原因:Union-Findを知らなかった
以上。(問題文読んですぐに模範解法を思いついたが、グループごとの要素数を扱う方法を知らなかったので切り捨ててしまった)
ということで新たなページを書いた(おまけでこのページも書いた)
abc213_d
(木の)DFSをまともに解いたことがなく、ノード間の移動を正確に正しく処理できなかった
このページを書き、自分の中で理解を深めた
典型90_058
フローチャートで循環に入る前の部分のことを忘れて周期計算をしてしまった
フローチャート描くのがめんどくさかったので、大阪環状線の路線図で代用(薬物依存の悪循環のイラストも同じ)
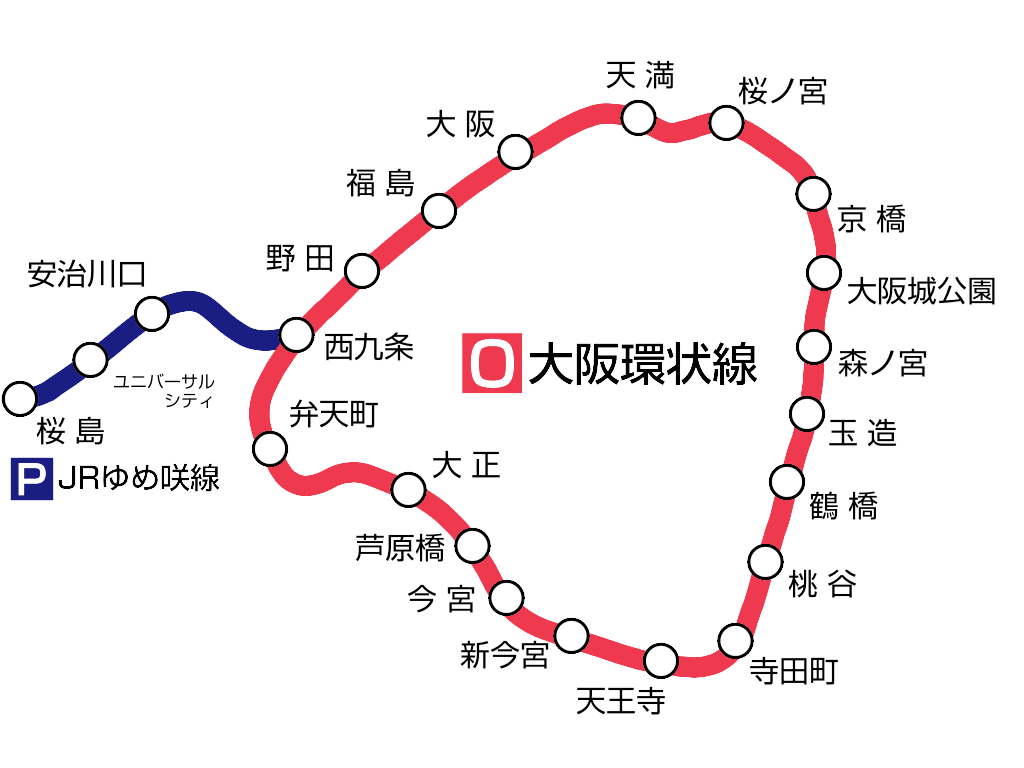
わかりやすい路線図をこのページから拝借
桜島始発の各駅列車が西九条から先、ひたすら大阪環状線を外回りで循環する場合、20駅目は大正
環状線は全部で19駅なので、20+19k駅目も大正(kは正の整数)
では20-19 = 1駅目は?答えは大正ではなくユニバーサルシティ
循環に入る前の例外処理を忘れるとここでWAする
K = K-(K//MOD)*MOD
K = K-(1+(K-20000)//MOD)*MOD
abc211_c
最後の最後に答えを求める部分でMODで割るのを忘れた
ans = 0
for i in range(len(mat[7])):
ans += mat[7][i][1]
ans = 0
for i in range(len(mat[7])):
ans = (ans + mat[7][i][1]) % MOD
abc211_d
都市間を道路を通って移動する問題で、**「各都市において次にどの都市に向かえるか」**をまとめず、入力で与えられた「各道路がどの都市を結んでいるか」の情報のみで解こうとした
この手法だと、各都市において該当する道路を毎回二分探索する必要があるため、無駄がある
よく使うし、都市間を道路を通って移動する問題の入力をチートシートに追加してもいいかも
for i in range(M):
A,B = map(int,input().split())
mat.append([A,B])
mat.append([B,A])
for i in range(M):
A,B = map(int,input().split())
root[A].append(B)
root[B].append(A)
arc123_c
足し算において、「前の桁からの繰り上がりが1あってその桁の合計の1桁目が0の場合は、繰り上がり前の1桁目は(-1ではなく)9である」という例外処理をしたにも関わらず、繰り上がりがなく1桁目が9であるケースと同様にその桁では繰り上がりが起きてないとして処理してしまった
より一般的にまとめると、「途中で一部ケースに対し例外処理を行ったにもかかわらず、その処理を行ったかどうかをその後区別せず同じものとして扱った結果バグが生じた」
if num == -1:
num = 9
if mat[MAX][num] == 1:
tmp += 1
kuriagari = 0
elif mat[MAX][num+10] == 1:
tmp += 1
kuriagari = 1
if num == -1:
num = 9
piyo = 1 # <- add
else:
piyo = 0 # <- add
if mat[MAX][num] == 1:
tmp += 1
kuriagari = 0
if piyo == 1: # <- add
kuriagari = 1 # <- add