LoginSignup
6
6

More than 3 years have passed since last update.

@ysuzuki19

ソートをC++で作って速度比較してみた。

Posted at

はじめに

ソートに興味を持ったので、Wikipediaを見ながらアルゴリズムを関数にしてみました。今回は、簡単に実装できるものを作成しましたが、今後他のソートも追加するかもしれません！
それぞれの関数は全部昇順ソートとし、vector型の配列を参照渡しするものとしました。
アルゴリズム自体についてはWikipediaに書いてある為、一言づつだけ記します。

いろいろなソートたち

バブルソート

ソートと言われてパッと思いつく方法。一番単純なのではないか。
$1\leq i\leq n$に対してv[i-1]<v[i]となるように交換し続け、交換する場所がなくなるまで1を繰り返す(ソート済み部分は交換チェックする必要はない)

bubble_sort
template<typename T> void bubbleSort(vector<T>& v){
  bool sorting = true;
  size_t sortedIdx = 0;
  while(sorting){
    sorting = false;
    for(size_t i=0; i<v.size()-1-sortedIdx; ++i){
      if(v[i]>v[i+1]){
        swap(v[i],v[i+1]);
        if(!sorting)sorting = true;
      }
    }
    sortedIdx++;
  }
}

選択ソート

未ソート部分から最小値を探索し、ソート済み部分の後ろに追加して、ソート済みとする。これを配列の$個数-1$回繰り返す。

selection_sort
template<typename T> void selectionSort(vector<T>& v){
  for(size_t i=0; i<v.size()-1; ++i){
    int minTemp = v[i];
    size_t minIdx = i;
    for(size_t j=i+1; j<v.size(); ++j){
      if(minTemp > v[j]){
        minTemp = v[j];
        minIdx = j;
      }
    }
    swap(v[i],v[minIdx]);
  }
}

シェーカーソート

バブルソートは片方向にループさせていたのに対して、シェイクするように逆方向にもループさせていく。

shaker_sort
template<typename T> void shakerSort(vector<T>& v){
  bool sorting = true;
  size_t sortedIdx = 0;
  while(sorting){
    for(size_t i=sortedIdx; i<v.size()-1; ++i){
      if(v[i]>v[i+1]){
        swap(v[i],v[i+1]);
      }
    }
    sorting = false;
    for(size_t i=v.size()-2-sortedIdx; i<v.size(); --i){
      if(v[i]>v[i+1]){
        swap(v[i],v[i+1]);
        if(!sorting)sorting = true;
      }
    }
    sortedIdx++;
  }
}

コムソート

バブルソートの改良版。バブルソートは隣同士の比較・交換であったのに対して、こちらではh個離れた要素と比較・交換する。このhは初期状態は要素数を1.3で割った数であり、ループごとに-1していく。

comb_sort
template<typename T> void combSort(vector<T>& v){
  size_t h = (v.size()*10)/13;
  bool is_sorted = false;
  while(!is_sorted){
    if(h==1)is_sorted = true;
    for(size_t i=0; i<v.size()-h; ++i){
      if(v[i]>v[i+h]){
        swap(v[i],v[i+h]);
        if(is_sorted)is_sorted = false;
      }
    }
    if(h>1) h = (h*10)/13;
    if(h==0) h = 1;
  }
}

ノームソート

挿入ソートを作ったつもりであったのだが、配列では挿入という動作ができなかった。挿入する代わりに、挿入する位置まで隣同士交換して移動という処理をするとノームソートになるようである。

norm_sort
template<typename T> void normSort(vector<T>& v){
  for(size_t i=1; i<v.size(); ++i){
    for(size_t j=i; j<v.size(); --j){
      if(v[j-1]>v[j]){
        swap(v[j-1],v[j]);
      }
    }
  }
}

シェルソート

バブルソートの改良版。バブルソートは隣同士で比較・交換していたのだが、シェルソートは幅$h$離れた要素同士をグループとして比較・交換する。ここで、$h_{i+1}=3h_i + 1$とすると速いらしい。

shell_sort
template<typename T> void shellSort(vector<T>& v){
  size_t h = 1;
  while(1){
    size_t nexth = 3*h + 1;
    if(nexth<v.size()) h = nexth;
    else break;
  }
  bool is_sorted = false;
  while(!is_sorted){
    if(h==1)is_sorted = true;
    for(size_t i=h; i<v.size(); ++i){
      for(size_t j=i; j>=h; j-=h){
        if(v[j-h]>v[j]){
          swap(v[j-h],v[j]);
          if(is_sorted)is_sorted = false;
        }
      }
    }
    h = (h-1)/3;
    if(h==0) h = 1;
  }
}

上記のソートを試す

きちんとソートできているかも不安だった為、それを確認する関数checkSorted()でチェックしつつstd::chronoクラスで時間測定もして結果を出力した。ここでは、ソートする数値について、int型を用い、あたいの範囲は$0$以上$10000$以下とした。

main.cpp
#include <iostream>
#include <vector>
#include <cmath>
#include <chrono>
using namespace std;

constexpr int VECTOR_MAX = 10000;
#define debug(var)  do{std::cout << #var << " : "; view(var);}while(0)
template<typename T> void view(const vector<T>& v){ for(const auto& e : v) std::cout << e << " "; std::cout << std::endl; }
template<typename T> void generateVector(vector<T>& v){ for(auto& e : v) e = rand()%VECTOR_MAX; }

template<typename T> bool checkSorted(const vector<T>& v){
  bool is_sorted = true;
  int temp = 0;
  for(const auto& e : v){
    if(temp > e) is_sorted = false;
    temp = e;
  }
  return is_sorted;
}

template<typename T> void bubbleSort(vector<T>& v){
  bool sorting = true;
  size_t sortedIdx = 0;
  while(sorting){
    sorting = false;
    for(size_t i=0; i<v.size()-1-sortedIdx; ++i){
      if(v[i]>v[i+1]){
        swap(v[i],v[i+1]);
        if(!sorting)sorting = true;
      }
    }
    sortedIdx++;
  }
}

template<typename T> void selectionSort(vector<T>& v){
  for(size_t i=0; i<v.size()-1; ++i){
    int minTemp = v[i];
    size_t minIdx = i;
    for(size_t j=i+1; j<v.size(); ++j){
      if(minTemp > v[j]){
        minTemp = v[j];
        minIdx = j;
      }
    }
    swap(v[i],v[minIdx]);
  }
}

template<typename T> void shakerSort(vector<T>& v){
  bool sorting = true;
  size_t sortedIdx = 0;
  while(sorting){
    for(size_t i=sortedIdx; i<v.size()-1; ++i){
      if(v[i]>v[i+1]){
        swap(v[i],v[i+1]);
      }
    }
    sorting = false;
    for(size_t i=v.size()-2-sortedIdx; i<v.size(); --i){
      if(v[i]>v[i+1]){
        swap(v[i],v[i+1]);
        if(!sorting)sorting = true;
      }
    }
    sortedIdx++;
  }
}

template<typename T> void combSort(vector<T>& v){
  size_t h = (v.size()*10)/13;
  bool is_sorted = false;
  while(!is_sorted){
    if(h==1)is_sorted = true;
    for(size_t i=0; i<v.size()-h; ++i){
      if(v[i]>v[i+h]){
        swap(v[i],v[i+h]);
        if(is_sorted)is_sorted = false;
      }
    }
    if(h>1) h = (h*10)/13;
    if(h==0) h = 1;
  }
}

template<typename T> void normSort(vector<T>& v){
  for(size_t i=1; i<v.size(); ++i){
    for(size_t j=i; j<v.size(); --j){
      if(v[j-1]>v[j]){
        swap(v[j-1],v[j]);
      }
    }
  }
}

template<typename T> void shellSort(vector<T>& v){
  size_t h = 1;
  while(1){
    size_t nexth = 3*h + 1;
    if(nexth<v.size()) h = nexth;
    else break;
  }
  bool is_sorted = false;
  while(!is_sorted){
    if(h==1)is_sorted = true;
    for(size_t i=h; i<v.size(); ++i){
      for(size_t j=i; j>=h; j-=h){
        if(v[j-h]>v[j]){
          swap(v[j-h],v[j]);
          if(is_sorted)is_sorted = false;
        }
      }
    }
    h = (h-1)/3;
    if(h==0) h = 1;
  }
}

int main() {
  double sortTime;
  std::chrono::system_clock::time_point timeStt, timeEnd;
  size_t size = 10000;
  vector<int> v(size);
  generateVector(v);

  //bubble sort
  vector<int> v_bubble = v;
  timeStt = std::chrono::system_clock::now();
  bubbleSort(v_bubble);
  timeEnd = std::chrono::system_clock::now();
  sortTime = std::chrono::duration_cast<std::chrono::microseconds >(timeEnd - timeStt).count();
  cout << "bubble sort : " << (checkSorted(v_bubble)? "OK" : "NG") << endl;
  cout << "bubble time[s] : " << sortTime/1000000 << endl;

  //selection sort
  vector<int> v_selection = v;
  timeStt = std::chrono::system_clock::now();
  selectionSort(v_selection);
  timeEnd = std::chrono::system_clock::now();
  sortTime = std::chrono::duration_cast<std::chrono::microseconds >(timeEnd - timeStt).count();
  cout << "selection sort : "  << (checkSorted(v_selection)? "OK" : "NG") << endl;
  cout << "selection time[s] : " << sortTime/1000000 << endl;

  //shaker sort
  vector<int> v_shaker = v;
  timeStt = std::chrono::system_clock::now();
  shakerSort(v_shaker);
  timeEnd = std::chrono::system_clock::now();
  sortTime = std::chrono::duration_cast<std::chrono::microseconds >(timeEnd - timeStt).count();
  cout << "shaker sort : "  << (checkSorted(v_shaker)? "OK" : "NG") << endl;
  cout << "shaker time[s] : " << sortTime/1000000 << endl;

  //comb sort
  vector<int> v_comb = v;
  timeStt = std::chrono::system_clock::now();
  combSort(v_comb);
  timeEnd = std::chrono::system_clock::now();
  sortTime = std::chrono::duration_cast<std::chrono::microseconds >(timeEnd - timeStt).count();
  cout << "comb sort : "  << (checkSorted(v_comb)? "OK" : "NG") << endl;
  cout << "comb time[s] : " << sortTime/1000000 << endl;

  //norm sort
  vector<int> v_norm = v;
  timeStt = std::chrono::system_clock::now();
  normSort(v_norm);
  timeEnd = std::chrono::system_clock::now();
  sortTime = std::chrono::duration_cast<std::chrono::microseconds >(timeEnd - timeStt).count();
  cout << "norm sort : "  << (checkSorted(v_norm)? "OK" : "NG") << endl;
  cout << "norm time[s] : " << sortTime/1000000 << endl;

  //shell sort
  vector<int> v_shell = v;
  timeStt = std::chrono::system_clock::now();
  shellSort(v_shell);
  timeEnd = std::chrono::system_clock::now();
  sortTime = std::chrono::duration_cast<std::chrono::microseconds >(timeEnd - timeStt).count();
  cout << "shell sort : "  << (checkSorted(v_shell)? "OK" : "NG") << endl;
  cout << "shell time[s] : " << sortTime/1000000 << endl;


  return 0;
}

結果がこちら

result_vector100
bubble sort : OK
bubble time[s] : 8.8e-05
selection sort : OK
selection time[s] : 3.9e-05
shaker sort : OK
shaker time[s] : 8e-05
comb sort : OK
comb time[s] : 1.8e-05
norm sort : OK
norm time[s] : 7.6e-05
shell sort : OK
shell time[s] : 9.3e-05

size=1000とした時の結果がこちら

result_vector1000
bubble sort : OK
bubble time[s] : 0.007869
selection sort : OK
selection time[s] : 0.003266
shaker sort : OK
shaker time[s] : 0.005937
comb sort : OK
comb time[s] : 0.000209
norm sort : OK
norm time[s] : 0.004639
shell sort : OK
shell time[s] : 0.005341

size=10000とした時の結果がこちら

result_vector10000
bubble sort : OK
bubble time[s] : 0.627583
selection sort : OK
selection time[s] : 0.191342
shaker sort : OK
shaker time[s] : 0.551535
comb sort : OK
comb time[s] : 0.00303
norm sort : OK
norm time[s] : 0.483497
shell sort : OK
shell time[s] : 0.502929

計算量オーダーについて

計算量オーダーは以下のようになっており、ここで作成したソートに対して

ソート名 計算時間
バブル $O(n^2)$
シェーカー $O(n^2)$
コム $O(n\log n)$
ノーム $O(n^2)$
選択 $O(n^2)$
シェル $O(n\log n^2)$

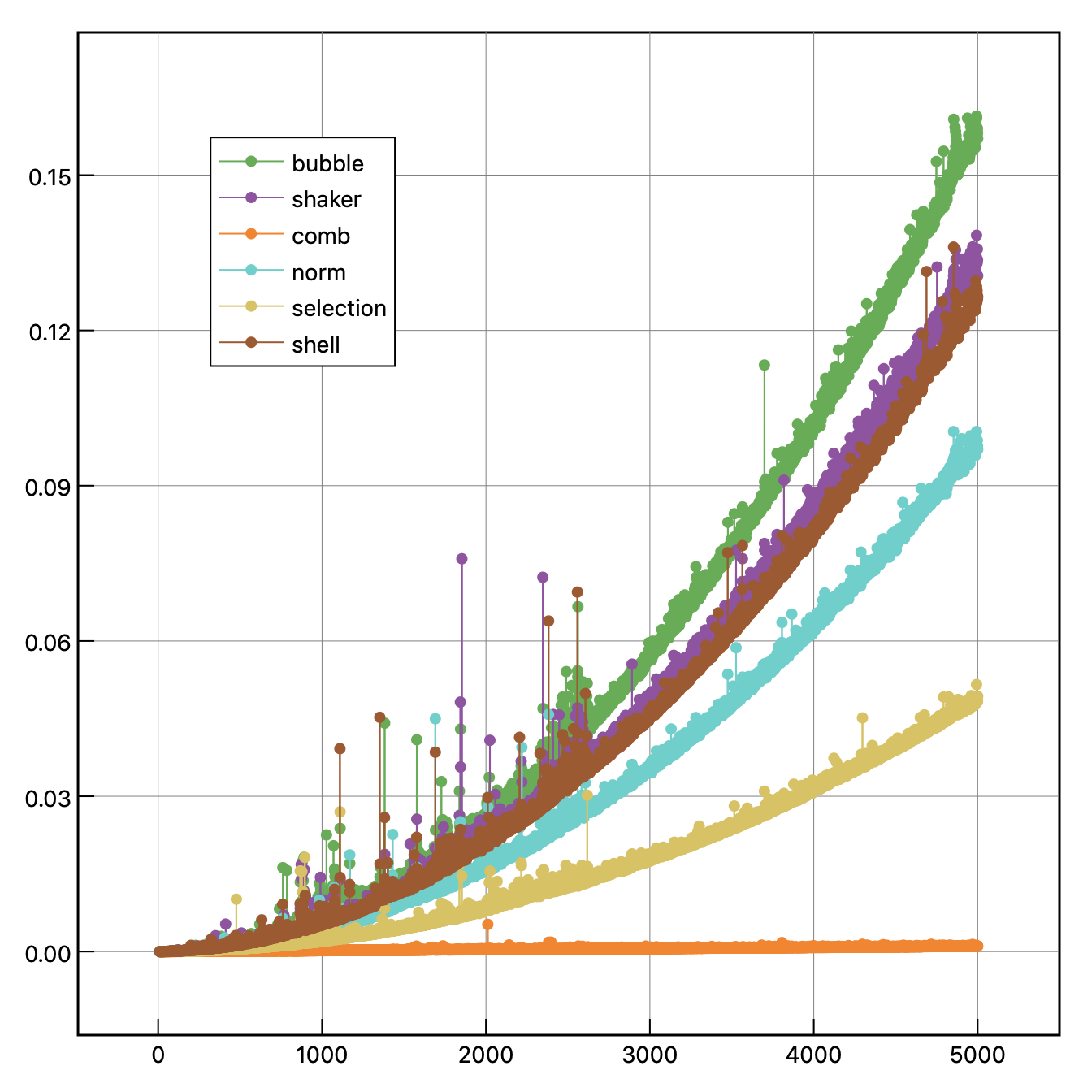
であるという。実際にmain.cpp内のsizeを$10<=size<=5000$の範囲で計算時間を保存したものが以下である。この時int型の数値の最大値は`100'とした。また、各データ数に対して全てのソート関数を終えた後に

check_sorted
main(){
...
if(!checkSorted(v_bubble)|| !checkSorted(v_selection)|| !checkSorted(v_shaker)|| !checkSorted(v_comb)|| !checkSorted(v_norm)|| !checkSorted(v_shell)) return -1;
...
}

の行を入れることで、ソートが完了していない場合は終了するようにした。

sortTime.png

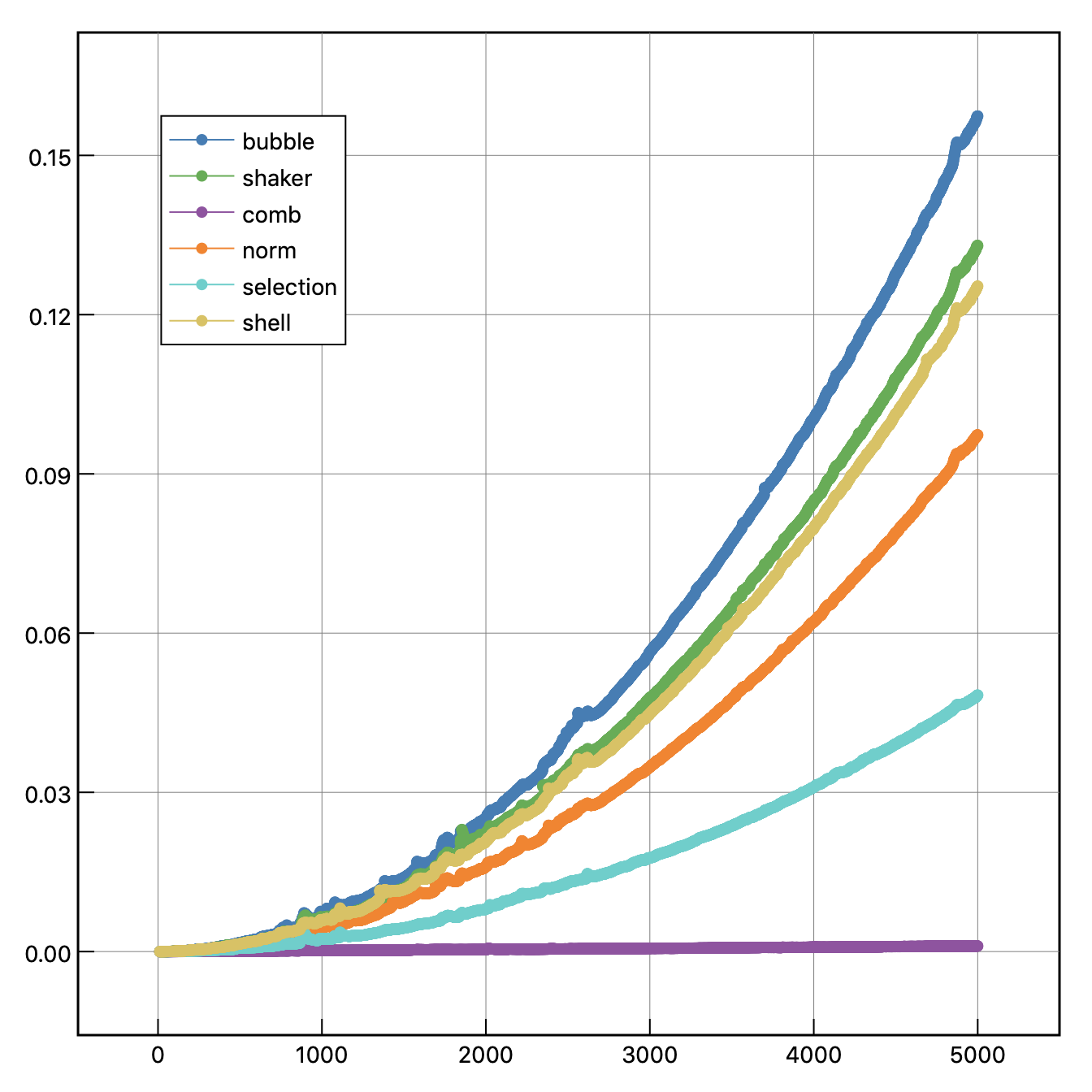
このグラフだと細かい振動が激しいので、時間測定で得た時間データ$a_i$に対して

b_{i+1}=rate\cdot a_{i+1}+(1.0-rate)\cdot b_{i}

の数式を適用してグラフの概形を取り出した時間データ$b_i$が以下である($b_0=0$とする)。

sortTime_lpf.png

  • コムソートがすごく速い。
  • バブルソートは気軽に実装できるが、動作は遅かった。
  • シェルソートが遅い気がしている。

おわりに

ここで作成したソートプログラムやそのサイズを動かしながら計算時間を求めるプログラム等はこちらに置いておきましたので、よかったら試してみてください！
今後気が向いた時に、他のソートも作って$n^2$と$n\log n$の比較もできたらと思いました。

6
6
2

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
6
6