はじめに
本記事は「KAN: Kolmogorov–Arnold Networks」の紹介をしています。
概要
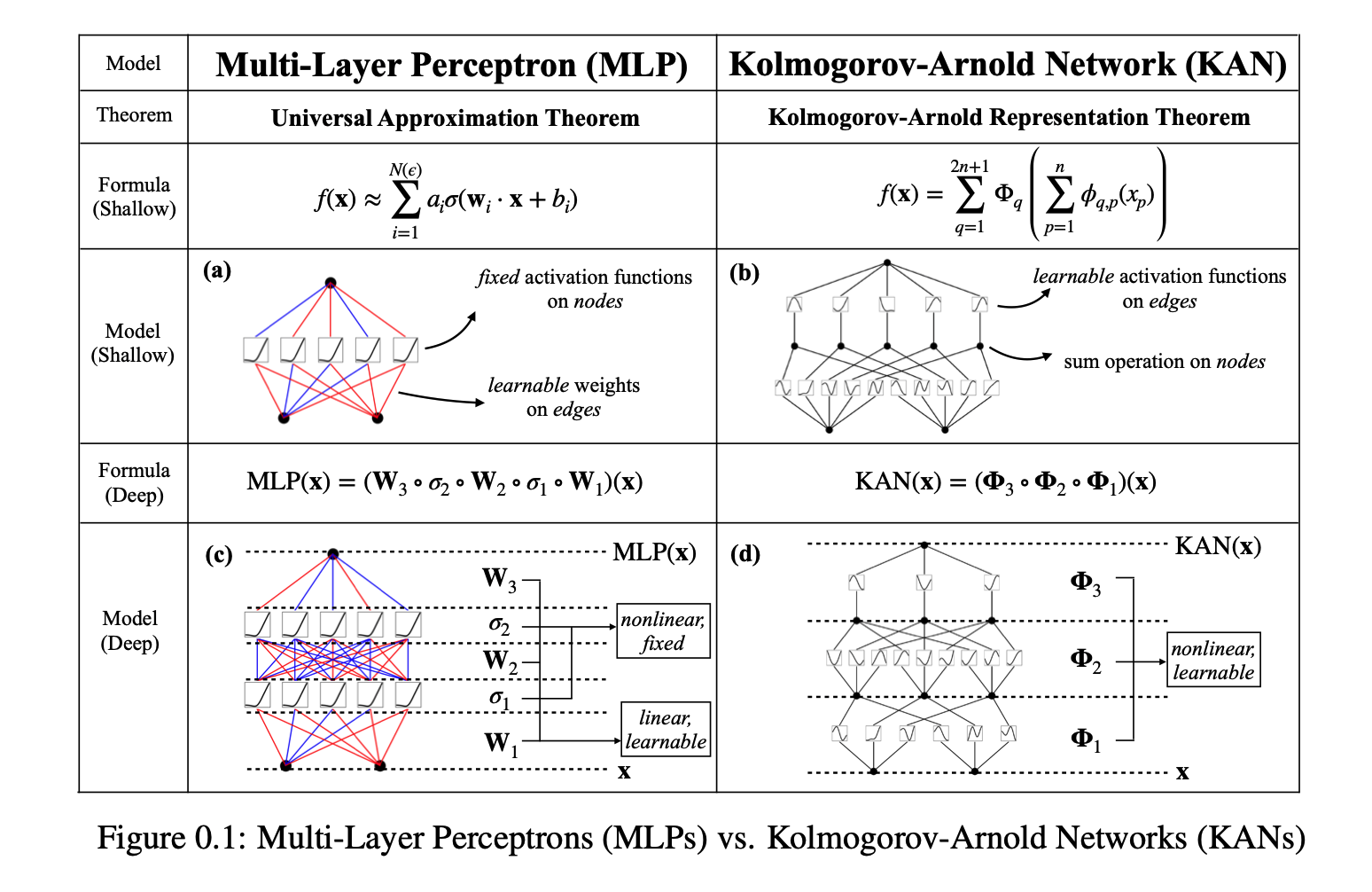
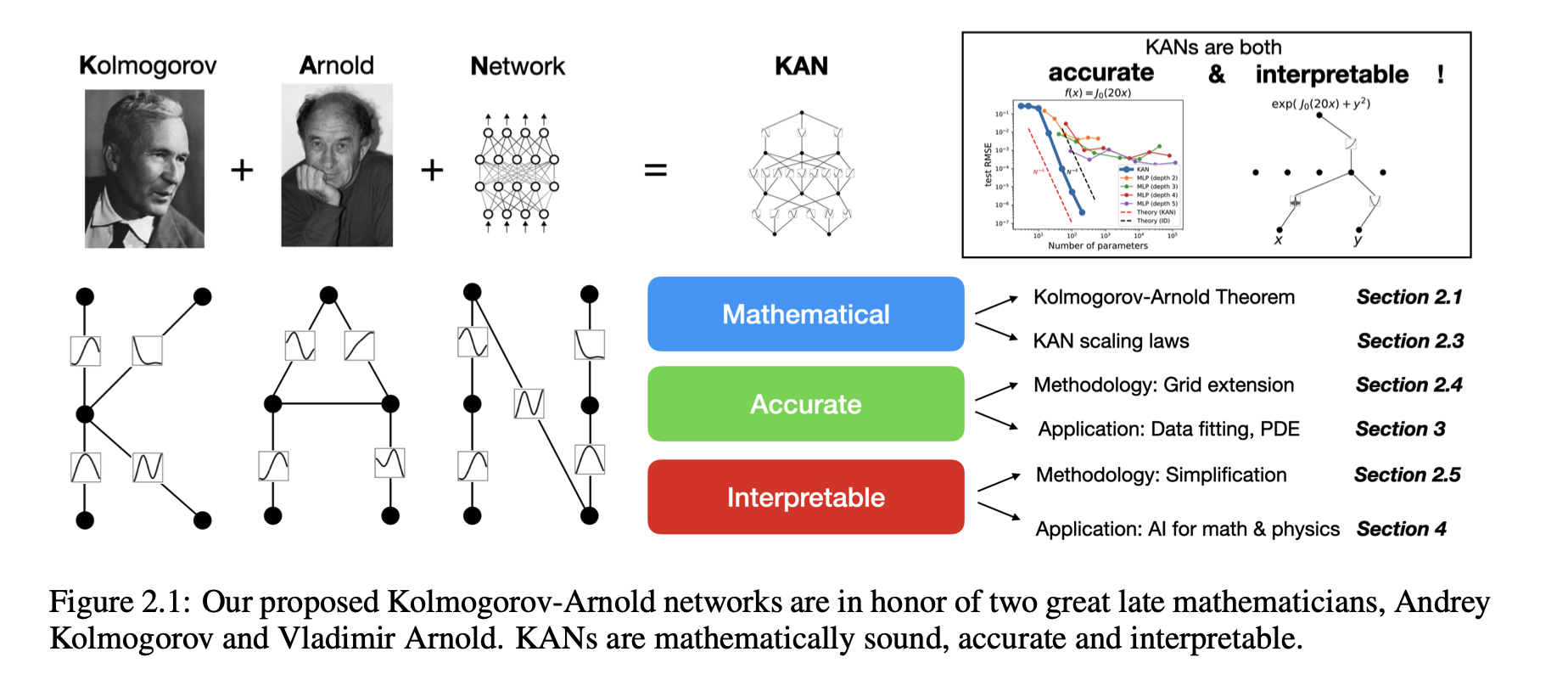
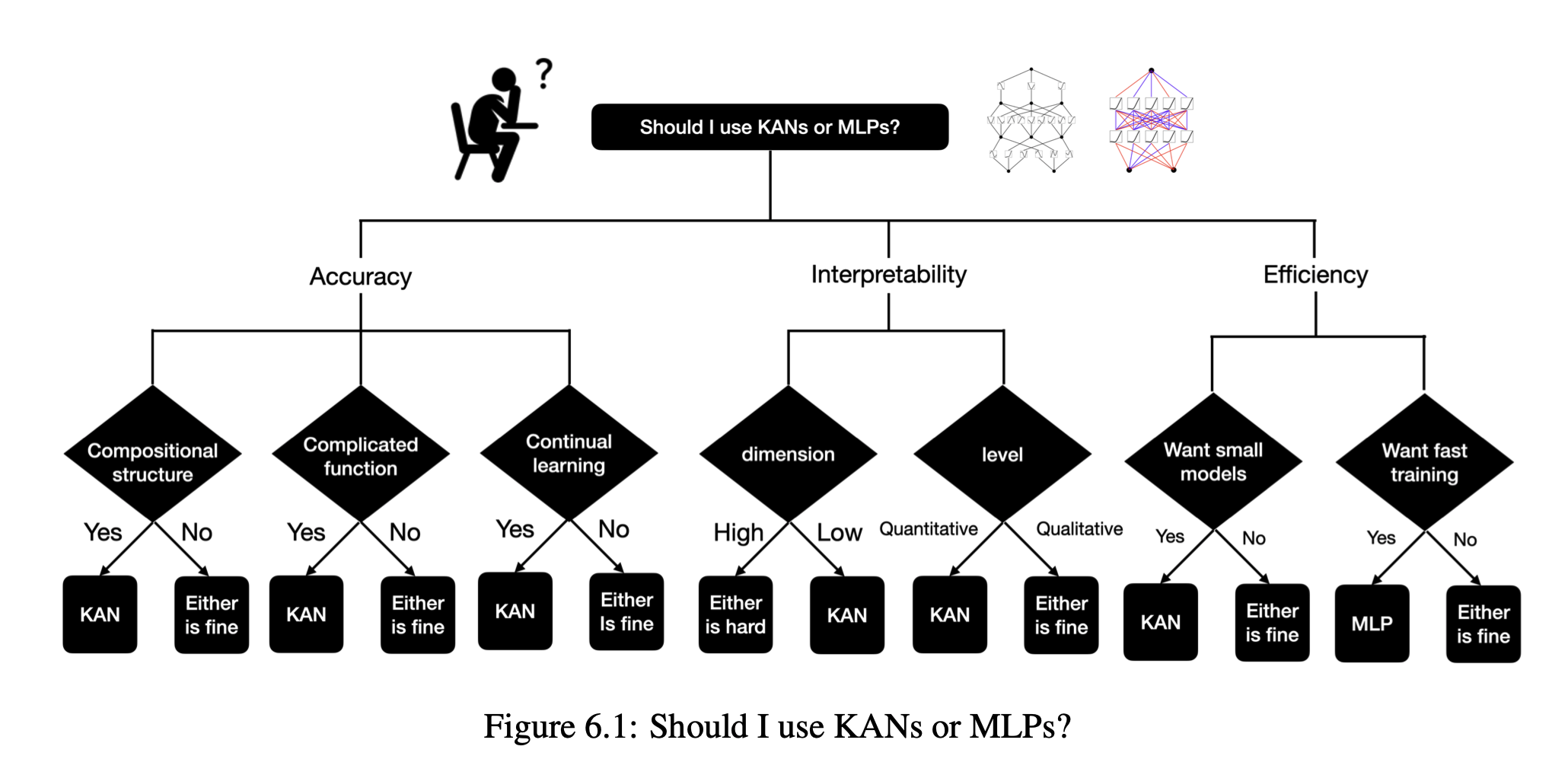
コルモゴロフ–アーノルド表現定理に着想を得て、我々はKolmogorov–Arnold Networks(KAN)を提案し、これは多層パーセプトロン(MLP)の有望な代替手段となります。MLPではノード(「ニューロン」)に固定の活性化関数が使用されますが、KANではエッジ(「重み」)に学習可能な活性化関数が適用されます。
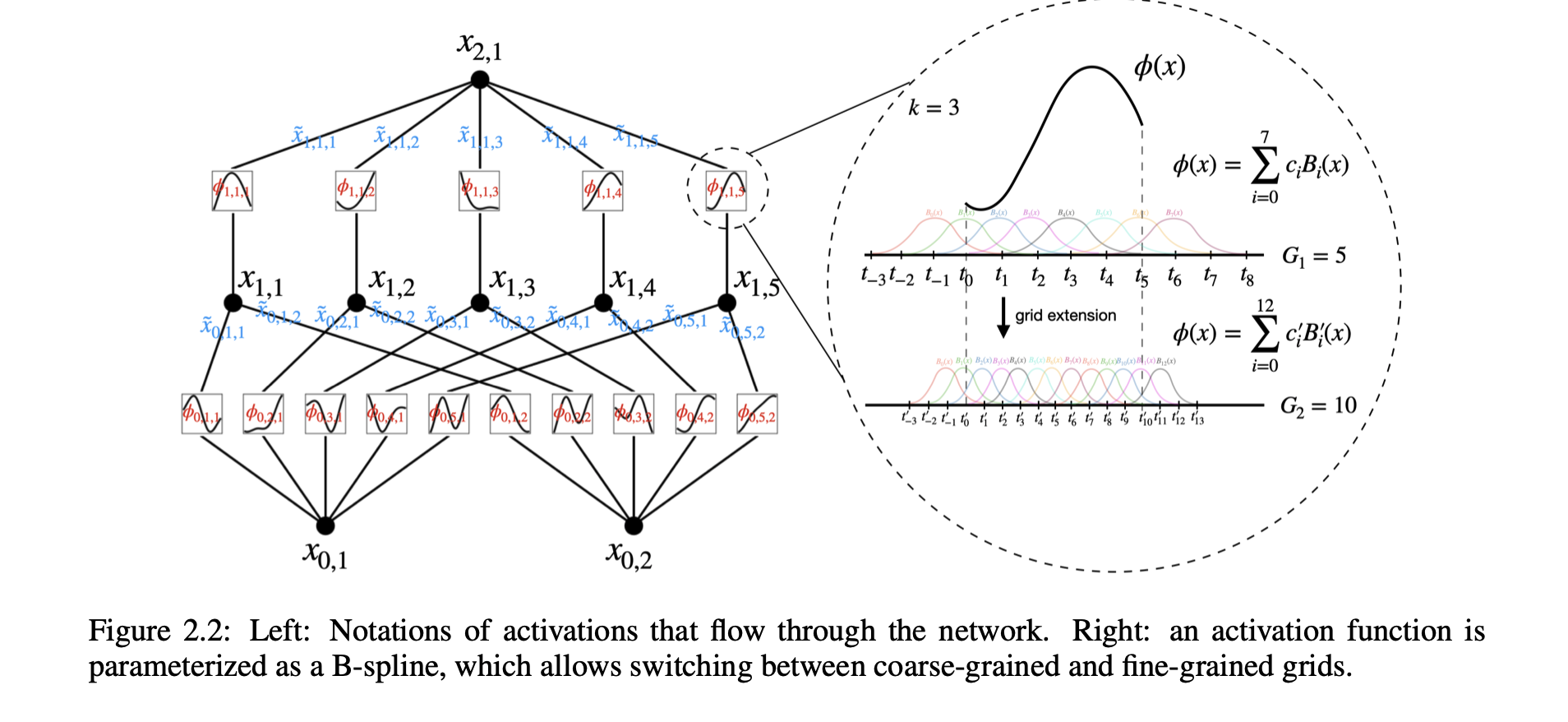
KANには線形の重みが全く存在せず、すべての重みパラメータはスプラインとしてパラメータ化された一変数関数に置き換えられています。この一見単純な変更により、KANは精度と解釈性の両面でMLPを上回ることを示しました。精度に関しては、データフィッティングや偏微分方程式の解法において、はるかに小規模なKANが、より大規模なMLPと同等かそれ以上の精度を達成できます。理論的および実証的に、KANはMLPよりも高速なニューラルスケーリング則を持っています。
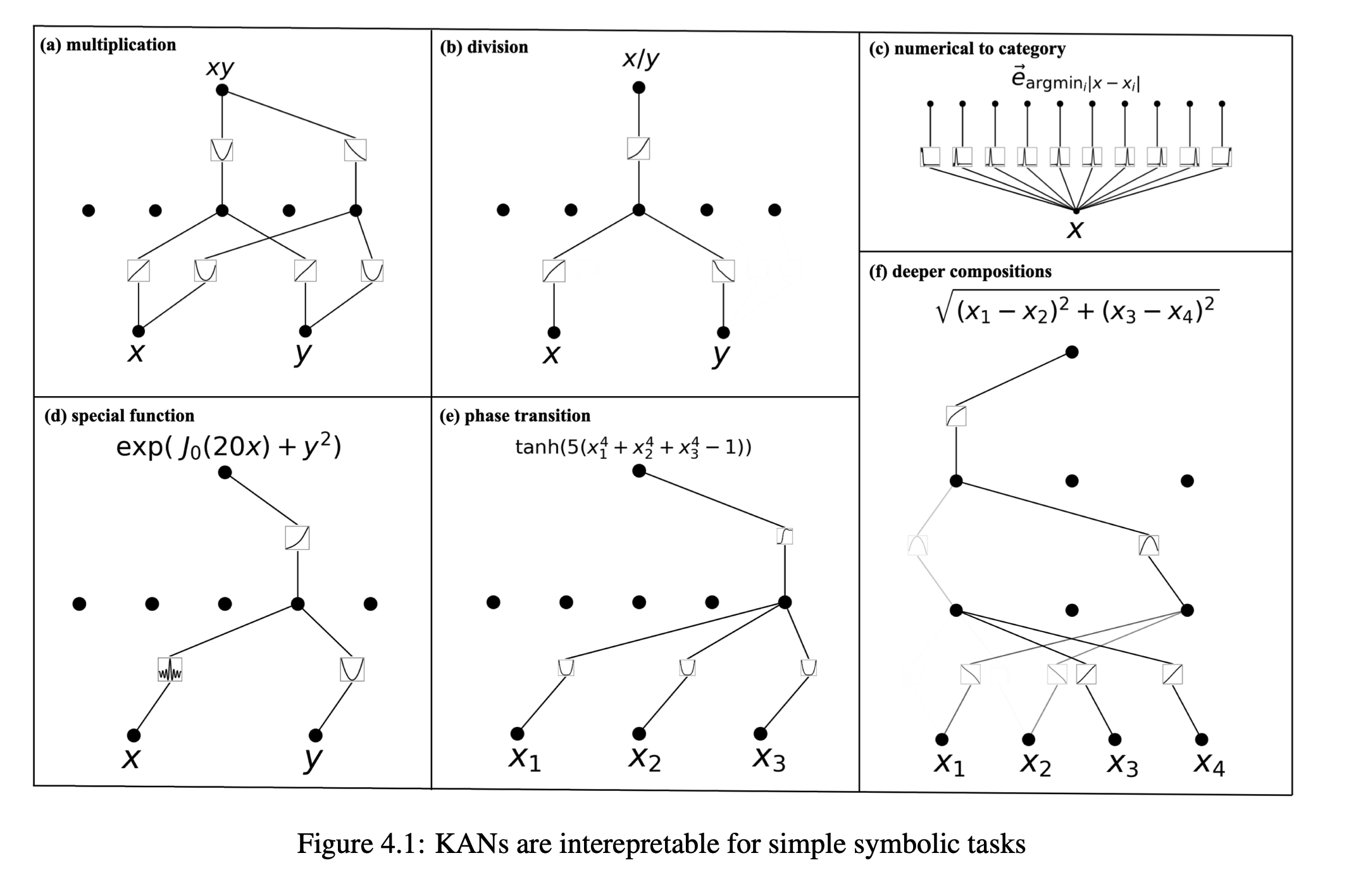
解釈性に関しては、KANは直感的に視覚化でき、人間のユーザーと容易に相互作用することが可能です。数学や物理学の2つの例を通じて、KANが科学者の数学的および物理的法則の(再)発見を支援する有用な協力者であることが示されました。
要約すると、KANはMLPの有望な代替手段であり、MLPに大きく依存している現在のディープラーニングモデルのさらなる改善の機会を提供します。 
用語の解説
- コルモゴロフ–アーノルド表現定理: 任意の連続関数を一変数関数の合成として表現できることを示す数学の定理で、関数近似の理論的基盤となります。
- 多層パーセプトロン(MLP): 複数の層からなるフィードフォワード型の人工ニューラルネットワークで、各層のニューロンは前の層の出力に重みをかけて線形結合し、活性化関数を通じて次の層に伝達します。
- スプライン: 関数近似や補間に用いられる分割多項式で、特に滑らかさと精度が求められる場合に使用されます。
- ニューラルスケーリング則: ニューラルネットワークの性能がモデルのサイズやトレーニングデータの量に応じてどのように変化するかを示す経験則で、モデルの設計や学習に関する指針を提供します。
- 偏微分方程式(PDE): 複数の独立変数に関する未知関数の偏微分を含む方程式で、物理学や工学などで多くの現象を記述するために用いられます。