概要
ビザンチン将軍問題のためのいくつかのコンセンサス・アルゴリズムが存在するが、特に分散型支払いシステムに関連する場合、ネットワーク内のすべてのノードが同期して通信するという要件が問題となり待ち時間が長くなってしまう。本研究では、大規模なネットワーク内で集合的に信頼できるサブネットワークを利用することにより、この要件を回避する新しいコンセンサスアルゴリズムを提示する。これらのサブネットワークに必要な「信頼」は実際には最小限であり、メンバーノードの原則的な選択によってさらに削減できることを示す。さらに、ネットワーク全体で合意を維持するために最小の接続性のみが要求されることも示す。結果として、レイテンシーの低いコンセンサスアルゴリズムが得られ、ビザンチン障害にもかかわらず頑健性が維持される。我々は、このアルゴリズムをRipple Protocolの一部として実装した。
導入
近年、分散型コンセンサスシステムにおける関心と研究は、分散型決済ネットワークに重点を置いて著しく増加している。そのようなネットワークは、中央集権的なソースによって制御されない、高速で低コストのトランザクションを可能にする。そのようなシステムの経済的な利点と欠点は、それ自体で多くの研究にふさわしいものだが、この作業は、すべての分散支払いシステムが直面しなければならない技術的課題のいくつかに焦点を当てている。これらの問題はさまざまであるが、それらを3つの主要カテゴリ、すなわち正当性、合意、および有用性に分類する。
正当性とは、分散システムが正しいトランザクションと不正なトランザクションの違いを識別できることが必要であることを意味する。伝統的な信託においては、これは機関間の信頼と、実際にその機関から来ていることを保証する暗号署名によって行われる。しかし、分散システムでは、ネットワーク内のすべてのメンバーの身元を知ることさえできないため、そのような信頼はない。したがって、正当性のための別の方法が利用されなければならない。
合意とは、分散された会計システムでありながら、単一のグローバルな真実を維持するという問題を指す。正当性の問題と類似してはいるが、その差異は、ネットワーク上の悪意のあるユーザーが不正な取引(正当性を無視して)を作成することができないものの、何らかの形で互いを認識していない複数の正しいトランザクションを作成できる可能性があり、その結果それらのトランザクションが組み合わさり不正行為を生み出し得る点だ。たとえば、悪意のあるユーザーは同じタイムスタンプの2つのトランザクションを作成する。しかし、ユーザーのアカウントには、どちらか一つのトランザクションを完了できるだけの資金しかない。したがって、それ自体では各トランザクションは正確であるが、分散ネットワーク全体が両者を認識しないように同時に実行されると、一般に「二重支出問題」[1]と呼ばれる明らかな問題が生じる。したがって、"同意”の問題は、グローバルに認識されたトランザクションの1組だけがネットワーク内に存在するという要件として要約することができる。
有用性は、やや抽象的な問題であり、我々は一般的に分散支払いシステムの「便利さ」として定義するが、実際には単純にシステムのレイテンシーとまとめられる。たとえば、正確で合意がとれてはいるが、トランザクションの処理に一年かかる分散システムは、支払いシステムとしては明らかに破綻している。有用性の別の側面として、正当性および合意プロセスに参加するために必要なコンピューティングパワーのレベル、またはエンドユーザーがネットワークで不正使用を避けるために必要とされる技術的な能力が含まれるだろう。
これらの問題の多くは、 "ビザンチン将軍問題" [2]と呼ばれる問題を通じて、現代の分散コンピュータシステムが登場するずっと前から研究されてきた。この問題では、将軍たちはそれぞれ軍の一部を支配し、お互いにメッセンジャーを送ることによって攻撃計画を調整する必要がある。将軍が不慣れで敵対的な地域にいるため、メッセンジャーは目的地に到達できない場合がある(分散ネットワーク内のノードが失敗するか、意図したメッセージの代わりに破損したデータを送信するように)。この問題のもう一つの側面は、将軍の中には個人であるか共謀してるかは不明だが裏切り者が潜んでおり、忠実な将軍の元に失敗する運命にある偽の計画を作り出すことを意図したメッセージが届くかもしれない、というものだ(分散システム上の悪意あるメンバーが不正なトランザクションをシステムに受け入れさせようとしたり、同一の正常なトランザクションを複数送信して二重支払いを引き起こそうとしたりするのと同様に)。したがって、分散型決済システムは、通常の障害に対しても、あるいはネットワーク内の複数のソースから発生しうる、いわゆるビザンチン将軍問題に対しても堅牢でなければならない。
この論文では、分散支払いシステムの1つの特定の実装、すなわちRipple Protocolを分析する。我々はこの、前述した正当性、合意、有用性の目標を達成するために調整されたアルゴリズムに焦点を当て、これらの目標が納得感のある所定の許容閾値内で実現されていることを確認する。また、このコンセンサスプロセスをシミュレートするコードを提供する。このコードはネットワークのサイズや悪意のあるユーザーの数、メッセージ送信のレイテンシーを調整可能だ。
2. Definitions, Formalization and Previous Work
まずRipple Protocolのコンポーネントを定義することからはじめる。正当性や合意、有用性と言った要素を証明するために、これらの要素を公理として定式化する。これらの要素すべてをまとめると「コンセンサス」という概念となる。つまり、「ネットワーク上のノードが正しい合意に至る」状態のことである。次に、コンセンサスアルゴリズムに関する幾つかの先行研究に言及し、その後我々の定式化したフレームワークの中でRipple Protocol におけるコンセンサスの目標について述べる。
2.1 Ripple Protocolのコンポーネント
Rippleネットワークの説明について、まず下記の用語を定義することから始める。
- サーバー: サーバーとは、コンセンサスプロセスに参加するためのRippleサーバー・ソフトウェアを実行するものである(ユーザー資金の送受信のみを行うRippleクライアント・ソフトウェアとは異なる)。
- レジャー(台帳): レジャーは各ユーザの口座にある通貨の金額を記録したものでネットワークの「真実の根拠」を表している。レジャーはコンセンサスプロセスを成功裏に通貨したトランザクションで、々更新される。
- Last-Closed Ledger: Last-Closed Ledgerはコンセンサスプロセスによって批准された最新のレジャーであり、ネットワークの最新の状態を表す。
- Open Ledger: Open Ledgerはノードの現在の動作状態である(すべてのノードが自分のOpen Ledgerを管理する)。 特定のサーバのエンドユーザーによって作られたトランザクションはそのサーバーのOpen Ledgerに適用されるが、コンセンサスプロセスを通過するまで、トランザクションは最終的なものとはみなされない。コンセンサスプロセスを通過すると、Open LedgerはLast-Closed Ledgerとなる。
- ユニークノードリスト(UNL): 各サーバーsはユニークノードリストを管理する。このリストはsがコンセンサスを決定する時に照会する他のサーバーの一覧である。sの管理するUNLのメンバーの投票のみが(ネットワーク上のすべてのノードではなく)、コンセンサスを決定する時に評価される。したがってUNLはネットワークのサブセットを表し、集合的に見ると、ネットワークを欺く試みで結託しないとsに「信頼されている」。ここでの「信頼」の定義では、UNLの各メンバーが信頼されている必要がないことは注記しておく(セクション3.2を参照)。
- プロポーザー: すべてのサーバーは、コンセンサスプロセスに含めるトランザクションをブロードキャストでき、すべてのサーバーは、新しいコンセンサスラウンドが始まった時にすべての有効なトランザクションを含めるように試みる。しかし、コンセンサスプロセスの間、sは自身のUNLに含まれるサーバからの提案のみを考慮する。
2.2 Formalization
ネットワーク内のノードの内、正直でエラーなく動作するものを指してnonfaultyという用語を使用する。逆にfaultyノードとはエラーが発生したノードを指し、エラーとは正当なもの(データの破損、実装エラーなど)かあるいは悪意のあるもの(ビザンチン将軍問題等)である。トランザクションの正当性を検証する、という概念を単純な二分決定問題に還元する。つまり、各ノードは自身に与えられた0か1か、という情報からトランザクションの正当性を決定しなければならない。
Attiya, Dolev, and Gill, 1984 [3]にあるように、我々は下記3つの公理に従ってコンセンサスを定義する。
- C1: すべてのnonfaultyノードは有限時間内に決定を下す
- C2: すべてのnonfaultyノードは同じ決定に達する
- C3: 0と1はすべてのnonfaultyノードにおいてあり得る値である。(これにより、提示された情報に関係なく、すべてのノードが0または1を決定する簡単な解決法が除外される)
2.3 既存のコンセンサスアルゴリズム
ビザンチン障害に際してコンセンサスを達成するアルゴリズムについて、多くの研究が行われてきた。この前の研究では、ネットワーク内のすべての参加者が事前に知られておらず、メッセージが非同期で送信され(個々のノードが決定に達するまでの時間に制限はない)、コンセンサスが強いと弱いという概念が区別されている場合の拡張が含まれていた。
コンセンサスアルゴリズムに関するこれまでの研究の関連する成果の1つはFisher、Lynch、Patterson [1985] によるもので、非同期の場合、コンセンサスアルゴリズムにとって、non-terminationは(たとえたった一つの障害が起因であったとしても)常に可能性の一つである、と証明した。これは、収束を確実にするために時間ベースヒューリスティックの必要性を導入する(or at least repeated iterations of non-convergence)。第3章では、Ripple Protocolのこれらのヒューリスティックを説明する。
コンセンサスアルゴリズムの強みは、通常許容される欠陥プロセスの割合で測定される。どのビザンチン将軍問題(同期性と既知の参加者を仮定している)の解決策でも、$(n-1)/3$ビザンチン障害以上、またはネットワークの33%が悪意のある行動を行った場合に耐えられないことは証明可能だ。ただし、このソリューションでは、ノード間で配信されるメッセージ(デジタル署名)の検証可能な信頼性を必要としない。メッセージの偽造不可能性に対する保証が可能な場合、アルゴリズムは、同期の場合にはるかに高い耐障害性を備えて存在する。
非同期の場合、ビザンチンのコンセンサスに対してより複雑なアルゴリズムがいくつか提案されている。FaB Paxos [5]は、n個のノードから成るネットワークで$(n-1)/5$個のビザンチン障害を許容し、悪意を持った共謀もネットワーク内のノードの20%まで許容する。Attiya、Doyev、およびGill [3]は、$(n-1)/4$、またはネットワークの最大25%の障害に耐えることができる非同期の場合のフェーズアルゴリズムを紹介している。最後に、Alchieriら 2008 [6]は、$(n-1)/3$失敗の許容範囲の最大限度を制限しながら、未知の参加者が含まれていても非同期の場合にビザンチンコンセンサスを達成するBFT-CUPを提示するが、基盤となるネットワークの接続性に関して追加の制約を必要とした。
2.4 コンセンサスの形式的な目標
この論文における我々の目標は、Ripple Protocolで利用されているコンセンサスアルゴリズムが各元帳締結時に合意を達成し(すべてのトランザクションが否決されるという些細なコンセンサスだったとしても)、些細な合意がビザンチン障害に直面しても既知の確率で達成されることを示すことである。ネットワーク内の各ノードは、信頼できるノードセット(UNL内の他のノード)からの提案に投票するだけであり、各ノードが異なるUNLを持つ可能性があるため、各UNLの内容に関わらず、すべてのノード間でただ一つのコンセンサスに達する、ということも示す。この目標は、ネットワーク内の「フォーク」を防止することとにもなる。これは、2つの互いに疎なノードセットがそれぞれコンセンサスに独立して到達し、2つの異なる最後の閉鎖元帳が各ノードセットのノードによって観察される状況だ。
最後に、$(n-1)/5$の失敗に直面してRipple Protocolがこれらの目標を達成できることを示す。これは文献の中で最も強力な結果ではないが、Ripple Protocolには、その有用性を大きく向上させる他の望ましい機能があることも説明する。
3. Ripple Consensus Algorithm
Ripple Protocol Consensus Algorithm(RPCA)は、ネットワークの正当性と合意を維持するために、すべてのノードによって数秒毎に適用されている。コンセンサスに達すると、現在のレジャーは「閉鎖」とみなされ、最後に閉鎖されたレジャーとなる。コンセンサスアルゴリズムが成功し、ネットワークにフォークが存在しないと仮定すると、ネットワーク内のすべてのノードが維持する最後に閉鎖されたレジャーは同一になる。
3.1 定義
RPCAはラウンド形式で進行する。各ラウンドは下記のように進む。
- 最初に、各サーバは、まだ適用されていないコンセンサスラウンドの開始前に見た有効なすべてのトランザクションを取る(これには、サーバのエンドユーザによって開始された新しいトランザクション、以前のコンセンサスプロセスから保持されたトランザクションなどが含まれる)。そしてそれを「候補セット(candidate set)」と呼ばれるリスト形式で公開する。
- 各サーバーはUNL上のすべてのサーバーの候補セットを統合し、すべてのトランザクションの真偽に投票する。
- 「yes」票の最低割合以上を受け取ったトランザクションは、次のラウンドがあれば次のラウンドに渡されるが、十分な票を受け取っていないトランザクションは破棄されるか、または次のレジャーのコンセンサスプロセスの候補セットの最初に追加される。
- コンセンサスの最終ラウンドでは、サーバーのUNLのうち80%がトランザクションに同意する必要がある。この要件を満たすすべての取引がレジャーに適用され、そのレジャーがクローズされ、新しい最後のレジャーになる。
3.2 正当性
正当性を達成するためには、最大限のビザンチン障害を考えれば、欠陥のあるノードの数がその許容値を超えない限り、コンセンサスの間に不正な取引を確認することは不可能であることが示されなければならない。 RPCAの正当性を証明するのは直接的なものだ。サーバのUNLの80%がそれに同意した場合にのみ取引が承認されるため、UNLの80%が正当である限り、不正な取引は承認されません。したがって、ネットワーク内のn個のノードからなるUNLの場合、コンセンサスプロトコルは、下記を満たす場合正当性を維持する。
f \leq (n-1)/5
この時 $f$ はビザンチン障害の数である。事実、 $(n-1)/5+1$ のビザンチン障害に直面しても正当性は技術的に維持される。コンセンサスプロセスは失敗するが、依然として不正なトランザクションを確認することはできない。不正なトランザクションを確認するには $(4n+1)/5$ のビザンチン障害が必要となる。この第二の境界を「弱い正当性の境界(the bound for weak correctness)」と呼び、全社を「強い正当性の境界(the bound for strong correctness)」と呼ぶ。
コンセンサスの間に確認されたとしても、すべての「不正」トランザクションが脅威となるわけではないことにも注意が必要だ。たとえば、コンセンサスプロセス中に二重支払いのトランザクションが確認されたとしても、最初のトランザクションが適用された後で、資金が使用できなくなるため、2番目のトランザクションは失敗する。この堅牢性は、トランザクションが決定論的に適用され、コンセンサスがネットワーク内のすべてのノードが同じセットのトランザクションに決定論的ルールを適用していることを保証するためだ。
少々異なる分析のために、任意のノードが共謀し悪質なカルテルに参加する確率を $p_c$ と仮定し、 $p_c$ は以下の値とする。
p^*=\sum_{i=0}^{\lceil\frac{n-1}{5}\rceil}
\left( \begin{array}{r}
n \\ i
\end{array}\right)
p_c^i(1-p_c)^{n-i}
この確率はある $p_c$ の値に対して、悪質なカルテルのサイズがビザンチン障害の最大閾値を下回る可能性を表す。この尤度は2項分布であるため、 $p_c$ の値が20%を超えると、カルテルの予想サイズはネットワークの20%を超え、コンセンサスプロセスを妨害する。実際には、UNLは無作為に選択されるのではなく、むしろ $p_c$ を最小限に抑えるという意図がある。ノードは匿名ではなく暗号的に識別可能であるため、大陸、国、産業、イデオロギーなどの複合的観点からノードのUNLを選択すると、生成された $p_c$ の値は20%よりずっと低くなる。一例として、アンチ・デフォルマネーション・リーグとウェストボロ・バプテスト教会が共謀してネットワークを欺く可能性は確かにかなり低く、20%よりはるかに小さい。 UNLの $p_c$ が比較的大きくても正当性の角度は非常に高く、たとえば15%の場合、UNLのノード数が200であっても97.8%である。
$p_c$ の値が異なる場合のUNLサイズと不正確性の確率の相関関係は、図1に示されている。ここで、縦軸は、悪質なカルテルがコンセンサスを妨げる可能性を表しているため、値が低くなるほどコンセンサス成功の可能性が上がる。図からわかるように、10%という高い $p_c$ でも、UNLが100ノードを超えて増えるにつれて、コンセンサスが阻止される確率は非常に迅速に無視できる程度になる。
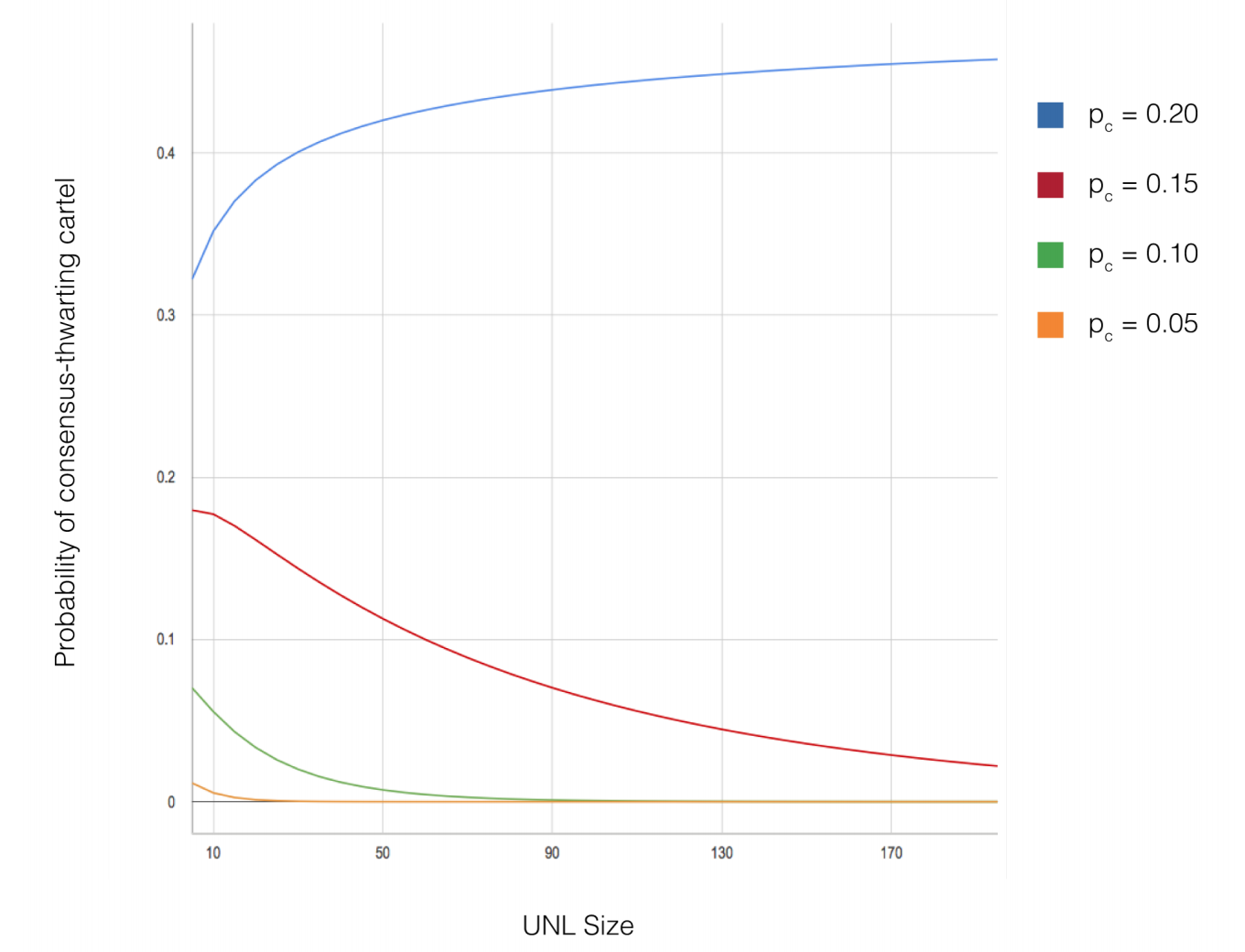
図1. 異なるそれぞれのPCの時に、悪質なカルテルがコンセンサスを阻止する可能性とUNLのサイズの相関関係。UNLのメンバーが他の人と共謀することを決定する確率。 ここでは値が低いほどコンセンサス成功率が高いことを示している。
3.3 合意
合意要件を満たすためには、UNLにかかわらず、すべての障害のないノードが同じトランザクションセットについてコンセンサスに達することを示す必要がある。各サーバのUNLが異なる可能性があるため、合意は正しさの証明によって本質的に保証されない。例えば、UNLのメンバーシップに制限がなく、UNLのサイズが $0.2 * n_{total}$ より大きくない場合($n_{total}$ はネットワーク全体のノードの数)、フォークが起きる可能性がある。これは、単純な例(図2)で示されている。 $0.2 * n_{total}$ より大きいUNLグラフ内の2つの派閥を想像してください。派閥とは、各ノードのUNLがノードの自己集合の集合であるノードの集合を意味する。これらの2つの派閥はいかなるメンバーも共有しないので、それぞれが互いに独立した正しいコンセンサスを達成し、合意に違反する可能性がある。 2つのクリークの接続性が $0.2 * n_{total}$ を超える場合、派閥間の不一致は、必要とされる80%合意閾値でコンセンサスに達することを妨げるので、フォークはもはや不可能である。

図2. UNLの派閥間でフォークを防止するために求められる接続数の例
合意を証明するために必要な接続数の上限は下記の数式で示される。
|UNL_i \cap UNL_j| \geq \frac{1}{5} max(|UNL_i|, |UNL_j|) \forall i, j
式(3)
この上限は、UNLの派閥のような構造を仮定する。すなわち、ノードは自身のUNLが自身の属する集合内の他のノードを含むような集合を形成する。この上限は、コンセンサスに必要な80%の閾値に達することが不可能になるので、2つの派閥が競合するトランザクションについてコンセンサスに達することができないことを保証する。 UNL間の間接的なエッジも考慮に入れると、より厳密な境界が可能になる。例えば、ネットワークの構造が派閥のようなものではない場合、すべてのノードのUNLの絡み合いが大きくなるため、フォークははるかに難しくなる。
興味深いのは、交差するノードの性質について何も仮定していないことだ。 2つのUNLの重なる部分には障害ノードが含まれていてもよいが、それは交差部分のサイズが合意を保証するために必要な境界より上である場合に限る。また、障害ノードの総数が強い正当性を満たす境界より下でなくてはならない。この時、両方の正当性と合意が達成される。つまり、合意はノードの重なりのサイズにのみ依存し、正常ノードの重なりのサイズに依存しているわけではない。
3.4 有用性
有用性の多くの要素は主観的であるが、確実に実証できるものの一つは収束(convergence)である。コンセンサスプロセスは有限時間内に終了するためだ。
3.4.1 収束
収束は、「RPCAがレジャー上の強い正当性によりコンセンサスに達し、そしてレジャーがlast-closed ledgerになること」と定義する。技術的には、弱い正当性も依然としてアルゴリズムの収束を表しているが、これは些細な事例でのみ起こりうる収束である点に留意が必要だ。これは命題C3に違反し、またトランザクションは決して確認されないためだ。上記の結果から、最大 $(n-1)/5$ のビザンチン障害が起きても強い正当性は達成可能であること、そしてUNLの接続条件が満たされていればネットワーク全体で唯一のコンセンサスが得られることがわかる。残っているのは、これらの条件が満たされた時に有限時間内にコンセンサスに達するのを示すことだ。
コンセンサスアルゴリズム自体は決定論的であり、コンセンサスが終了する前に予め設定されたラウンド数 $t$ を有し、現在のトランザクションセットは承認されたか否かを宣言される(この時点でどのトランザクションも必要な80%の合意を達成しておらず、コンセンサスが些細なものであったとしても)。アルゴリズムの終了の制限要因はノード間の通信待ち時間である。この待ち時間を制限するために、ノードの応答時間は監視され、待ち時間が予め設定された境界 $b$ より大きくなるノードがすべてのUNLから除去される。これによりコンセンサスは $tb$ の上限で終了することが保証されるが、除去されるべきすべてのノードが除去された後、上記の正確さと合意のために説明された境界は最終的なUNLによって満たされなければならないことに注意することが重要だ。すべてのノードの初期UNLでこれらの条件は満たされていたとして、待ち時間の関係で幾つかのノードが除去されたとする。この時正当性と合意の保証は自動的に満たされるわけではなく、新しいUNLの集合によってみたされなければならない。
3.4.2 ヒューリスティックと手順
上述したように、コンセンサスアルゴリズムが収束することを保証するために、Rippleネットワーク内のすべてのノードでレイテンシに基づいたヒューリスティックが実施される。 さらに、RPCAに有用性を提供するいくつかのヒューリスティクスと手順がある。
-
すべてのノードは、コンセンサスの各ラウンドで2秒の制限時間内に初期候補セットを提案しなければならない。これはコンセンサスの各ラウンドに2秒の下限を導入するが、正常なレイテンシーを持つ全てのノードがコンセンサスプロセスに参加する能力を持つことを保証する。
-
投票はコンセンサスの各ラウンドでレジャーに記録されるので、検出しやすい悪意のある行為がみつかった場合にはノードにはフラグがたてられ ネットワークから除外される可能性がある。これらの削除されるノードには、すべてのトランザクションを否決するようなノードや、コンセンサスで検証されていないトランザクションを一貫して提案するようなノードが含まれる。
-
すべてのユーザーには、デフォルトのUNLが用意されている。これは、セクション3.2で説明した $p_c$ を最小限に抑えるために選択されている。 ユーザーは自分のUNLを選択することができるが、このノードの既定のリストでは、素朴な(知識の少ない?)ユーザーであっても、非常に高い確率で正確性と一致性を実現するこのコンセンサスプロセスに参加することが保証する。
-
ネットワーク分割検出アルゴリズムは、ネットワーク内の分岐を回避するためにも使用される。 コンセンサスアルゴリズムは、最後にlast-closed ledger上の取引が正しいことを証明しているが、接続の悪いネットワークの異なるサブセクションに複数のlast-closed ledgerが存在することを禁止してはいない。 このような分割が発生したかどうかを識別するために、各ノードはUNLのアクティブなメンバーのサイズを監視している。 このサイズが突然あらかじめ設定したしきい値を下回った場合、分割が発生している可能性がある。 UNLの大部分に一時的な待ち時間がある場合に誤検出を防止するために、ノードは「部分的な検証」を発行することが許可されている。これはトランザクションに対して処理や投票を行わないが、分断されたサブネットワーク上の別のコンセンサスプロセスではなく、このコンセンサスプロセスに参加していることを宣言するものだ。
-
RPCAを1回のコンセンサスで適用することは可能だが、合意のための最低要求割合を徐々に高めた複数のラウンドを80%の要件を満たす最終ラウンドの前に実施することで、より有用性を高めることができる。これらのラウンドは、ネットワークのトランザクションレートのボトルネックとなっている潜在ノードの検出を可能にする。これらのノードは、初期の要求が低いラウンドでは追従できるだろうが、ラウンドが進みしきい値が高まるにつれて追従できなくなり特定される。1ラウンドのコンセンサスの場合、80%の合意に達するトランザクションはごく少数であろうことから、これらの遅いノードも追従でき、ネットワーク全体のトランザクションレートが下がる可能性がある。
4. シミュレーションコード
提供したシミュレーションコードは、RPCAのラウンドを表現している。幾つかの機能はパラメータ化されている(ネットワーク内のノード数、悪意のあるノードの数、メッセージの待ち時間等)。シミュレータは完全な不一致から開始する(ネットワーク上の反芻雨のノードが最初に「はい」を提案し、残りの半分が「いいえ」を提案する)。その後、コンセンサスプロセスに進み、各段階でノードは自身のUNLメンバーの判断に基づきはい・いいえを変えていく。80%のしきい値に達すると、コンセンサスは達成される。"Sim.cpp"の冒頭で定義された定数の値を変え、異なる条件下でのコンセンサスプロセスについて理解することをおすすめする。
5. 議論
上記で概説した正当性、合意、有用性の条件を満たすRPCAについて説明してきた。Ripple Protocolは安全で信頼性の高いトランザクションを数秒のうちに処理することが可能だ。この秒数はコンセンサスの1ラウンド完了にかかる時間である。これらのトランザクションはセクション3で概説された範囲内で安全性が証明されている。これは非同期ビザンチンコンセンサスの手法の中で最も強力、というわけではないが、迅速な収束とネットワークのメンバーシップに柔軟性を与える。これらの特性を組み合わせることで、Ripple Networkは、安全性と信頼性の特性がよく理解された、高速かつ低コストのグローバル決済ネットワークとして機能することができる。
方程式1および3に記載された境界が満たされる限り、リップルプロトコルは確かに安全であることが示されているが、これらは最大限の限界であり、実際のネットワークはかなり厳しくない条件下であっても安全である可能性があることは注目に値する。ただし、これらの境界を満たすことはRPCA自体に固有のものではなく、すべてのユーザーのUNLを管理することによって満たされるものであることを認識することも重要だ。すべてのユーザーに提供される既定のUNLは既に十分だが、ユーザーがUNLに変更を加える場合は、上記の境界の知識を持って行う必要がある。さらに、式3の境界が確実に満たされ、その合意が常に満たされるように、グローバルネットワーク構造の監視が必要だ。
RPCAはその低レイテンシーな特性により、既存の高レイテンシーな手段では困難だった多くの金融取引を可能にする。そのため、分散支払いシステムにとって重要な前進になると確信している。
※謝辞と参考文献は割愛
文中のシミュレータはこちらです: https://github.com/ripple/simulator
Kotlinで写経してみました: https://github.com/yshrsmz/ripple-simulator-kt