線形回帰とは
説明変数(予測に利用するデータ)を使って、目的変数(予測するデータ)を予測する線形関数(予測モデル)を作る手法。
予測するためには予測モデルを作るための学習が必要。=教師あり学習
下の図の横軸が説明変数、縦軸が目的変数、赤点が得られたデータだとすると、青線が回帰式(学習から得られた予測モデル)となる。
この回帰式が作れたら、未知の説明変数が入ってきたら、その時の目的変数がどうなりそうか予測できるよねって感じ。

回帰式の作成の仕方は、最小二乗法(実際の目的変数の値と予測値との差の二乗(二乗誤差)を最小にする方法)を使う。
上図でいうと、赤点から青線へ向かってx軸の垂線を引くと、その長さが誤差となる。これをプラスマイナスの影響を考慮して二乗し、全て足した値を最小にするイメージ。
利用データ用意
ボストンの住宅価格のデータを使う。
import numpy as np
import pandas as pd
from pandas import Series, DataFrame
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_style('whitegrid')
%matplotlib inline
from sklearn.datasets import load_boston
boston = load_boston() # ボストンの住宅価格データの取得
# データフレームに変換
boston_df = DataFrame(boston.data)
boston_df.columns = boston.feature_names
boston_df['Price'] = boston.target
データの概要
boston_df[['RM', 'Price']].describe()
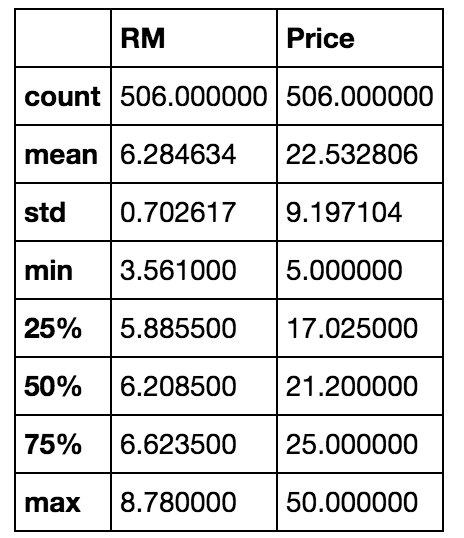
RMは、部屋の数。Priceが価格。
価格(目的変数)を予測するために、部屋の数を説明変数にしてみることとする。
簡単に部屋の数と価格の関係を見てみる。
# RM:部屋の数を横軸、Price:価格を縦軸に散布図を書いてみる
plt.scatter(boston_df['RM'], boston_df['Price'])
plt.xlabel('Number of rooms')
plt.ylabel('Price($1,000)')
plt.title('Scatter Plot')

散布図は上の通り。正の相関(部屋の数が増えれば、価格も増える関係)がありそう。
そこで相関係数を出してみる。
np.corrcoef (boston_df['RM'], boston_df['Price'])[0,1]
> 0.69535994707153925
相関係数0.695 強め。
なので、説明変数にRMを使うのは、筋は悪くはなさそう。
やってみる(単回帰)
1.seabornのlmplotで散布図と同時に回帰式を見てみる
sns.lmplot('RM', 'Price', data = boston_df)

めっちゃ簡単。seabornのlmplotのオプション:dataにDataFrameを渡し、X軸とY軸にDataFrameのカラム名を指定してあげるだけで線を作ってくれる。
2.numpyでやってみる
# numpyに喰わせるためにデータを変形 【※1】
X = np.vstack(boston_df.RM)
X = np.array([[value, 1] for value in X])
# 目的変数を用意
Y = boston_df.Price
# 線形回帰(np.linalg.lstsq)を実行してa:傾き、b:切片を取得。【※2】
a, b = np.linalg.lstsq(X, Y)[0]
# 散布図を書いて、そこに、得られた結果から回帰式を追記してみる。
plt.plot(boston_df.RM, boston_df.Price, 'o')
x = boston_df.RM
# 回帰式は、y = a * x + bで表現できるので、x軸にxを、y軸に a * x + bを指定。
plt.plot(x, a * x + b, 'r')
# xとy軸のラベル付与
plt.xlabel('Number of Room')
plt.ylabel('Price($1,000)')
numpyでの線形回帰の結果の図。赤線が得られた回帰式。

やってみる(重回帰)
sckit-learnを利用
単回帰が説明変数1つを利用するのに対し、重回帰は複数の説明変数を利用する。
boston_dfには、RM:部屋の数を含め13個の変数が存在するので、これらを使って価格を予測するモデルを作ってみる。
予測モデルを作る際は、学習(training)用とテスト(test)用に分ける方法をとる。
分ける理由は、「学習データだけで精度を見ると、未知のデータの予測に使えるかの判断ができない」から。
import sklearn
from sklearn.linear_model import LinearRegression # 線形回帰用
# 利用データの確認(CRIM〜Priceまでの14個のデータがある。Priceは目的変数なので、それ以外の13個を説明変数として利用してみる)
boston_df.info()
> <class 'pandas.core.frame.DataFrame'>
> Int64Index: 506 entries, 0 to 505
> Data columns (total 14 columns):
> CRIM 506 non-null float64
> ZN 506 non-null float64
> INDUS 506 non-null float64
> CHAS 506 non-null float64
> NOX 506 non-null float64
> RM 506 non-null float64
> AGE 506 non-null float64
> DIS 506 non-null float64
> RAD 506 non-null float64
> TAX 506 non-null float64
> PTRATIO 506 non-null float64
> B 506 non-null float64
> LSTAT 506 non-null float64
> Price 506 non-null float64
> dtypes: float64(14)
# Price以外の説明変数用DataFrame作成
X_multi = boston_df.drop('Price', 1)
X_multi.shape
> (506, 13)
# データをtrain用とtest用に分ける。
# sklearn.cross_validation.train_test_split(X, Y) でXを説明変数、Yを目的変数で指定するとサクッとわけてくれる。
X_train, X_test, Y_train, Y_test = sklearn.cross_validation.train_test_split(X_multi, boston_df.Price)
# 分割されたデータの数を確認
print(X_train.shape, X_test.shape, Y_train.shape, Y_test.shape)
> (379, 13) (127, 13) (379,) (127,)
# train用に379個、test用に127個に分割したことがわかる
# インスタンス生成
lreg = LinearRegression()
# 重回帰のモデル作成実施
lreg.fit(X_train, Y_train)
# 学習データとテストデータに対する予測実施
pred_train = lreg.predict(X_train)
pred_test = lreg.predict(X_test)
# 学習データとテストデータの平均二乗誤差を確認[average(実際の価格 - 予測値]^2)]
np.mean((Y_train - pred_train) ** 2)
> 20.5592370941859
np.mean((Y_test - pred_test) ** 2)
> 28.169312238554202
# 実際の正解と予測の残差をグラフで確認する。
# 横軸にtrainの結果、縦軸に誤差を表示
train = plt.scatter(pred_train, (pred_train - Y_train), c= 'b', alpha=0.5)
# 横軸にtestの結果、縦軸に誤差を表示
test = plt.scatter(pred_test, (pred_test - Y_test), c ='r', alpha=0.5)
# グラフの整え
# 誤差0の線を引く。
plt.hlines(y = 0, xmin = -1.0, xmax = 50)
# 凡例
plt.legend((train, test), ('Training', 'Test'), loc = 'lower left') # 凡例
# タイトル
plt.title('Residual Plots')
誤差プロット結果

黒の横線が誤差=0を表していて、それより上に点があれば誤差プラス、下にあれば誤差マイナス。この誤差が上下に均一に分布していれば、線形回帰でこの予測を解くのに適していると言える。
しかし、この誤差が偏った結果となっていると、線形回帰を適応すること自体を見直す方が良い。
補足
【※1】 npmpyで使う用のデータ整形について
単回帰の直線の式は、y = ax + bと表現できるが、これはベクトル表記に直すと、
y = Apと書き換えることができる。
Aとpはそれぞれ、以下となり、この内積がyになる。(y = a * x + b * 1)
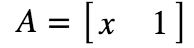

この形に整形をしている。
# boston_df.RMだと、1次元配列。
X = boston_df.RM
# Xの行列の形を確認(506行だけの1次元配列)
X.shape
> (506,)
X
>0 6.575
>1 6.421
>2 7.185
>...
>504 6.794
>505 6.030
>Name: RM, Length: 506, dtype: float64
numpyでこれを利用するためには、二次元配列に変えてあげないといけない。
# そこで二次元配列に変換するためにnp.vstackを使う。
X = np.vstack(boston_df.RM)
# Xの行列の形を確認(506行,1列の2次元配列)
X.shape
>(506, 1)
X
>array([[ 6.575],
> [ 6.421],
> [ 7.185],
> ・・・
> [ 6.794],
> [ 6.03 ]])
# さらにこれをA = [x, 1]に変換。Xの値を1次元目に、2次元目に固定値で1をセット
X = np.array([[value, 1] for value in X])
# Xの行列の形を確認(506行,2列の2次元配列)
X.shape
> (506, 2)
X
>array([[array([ 6.575]), 1],
> [array([ 6.421]), 1],
> [array([ 7.185]), 1],
> ...,
> [array([ 6.976]), 1],
> [array([ 6.794]), 1],
> [array([ 6.03]), 1]], dtype=object)
これで説明変数Xが[x 1]の形となり、めでたくnumpyで扱える形になる。
【※2】 np.linalg.lstsqについて
linalgがlinear Algebra(線形代数)の略称で、lstsqがLeast Square(最小二乗法)の略称。
返り値は、0行目:傾きと切片、1行:残差、2行目:説明変数のRank、3行目:説明変数の特異値(Singlar value)が入る。今回は傾きと切片を求めたいので[0]を指定。