SVMとは
Support Vector Machineの略。
学習データを用いて複数のクラスを分類する線を得て(学習モデル作成)、未知のデータ属する分類を推定する方法。
SVMでの分類の概要
元の次元から1つ低い平面を超平面と呼び、最適な超平面(分離面)を探す。
例えば下図だと、黒丸と白丸を分離する線(H1やH2)を引くことを実施する。
(この図は、X1とX2の二次元のデータを表しているが、H1やH2は直線で1次元。
もし三次元のデータがインプットなら、2次元で分類できる平面を探すことになる。)
最適な分離面の探し方は、マージンが最大になる分離面を探索する。
マージンとは、図でいう灰色の線で、各クラスの点から分離面への垂線の距離。
例えば、H1もH2も黒丸と白丸を分類する分離面と言えるが、マージンが大きいH2の方が分類力が高い。（H3は分類すらできてないので全然ダメ。）
カーネルトリック（カーネル法）
上の例は綺麗に分類できそうだけど、そうでない場合がほとんど。
そういう時に分離面を探す方法をカーネルトリックという。
例えば、下図だと、直線で赤丸と青丸を分離するのは困難。
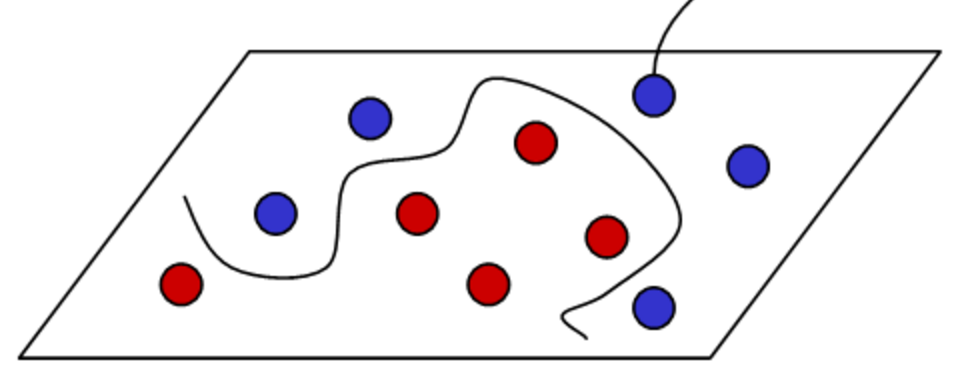
そこで綺麗に分離できるように、サンプルを別の空間[特徴空間]に写像(一定のルールで点を移動させる)して、その空間で分離面を探す。
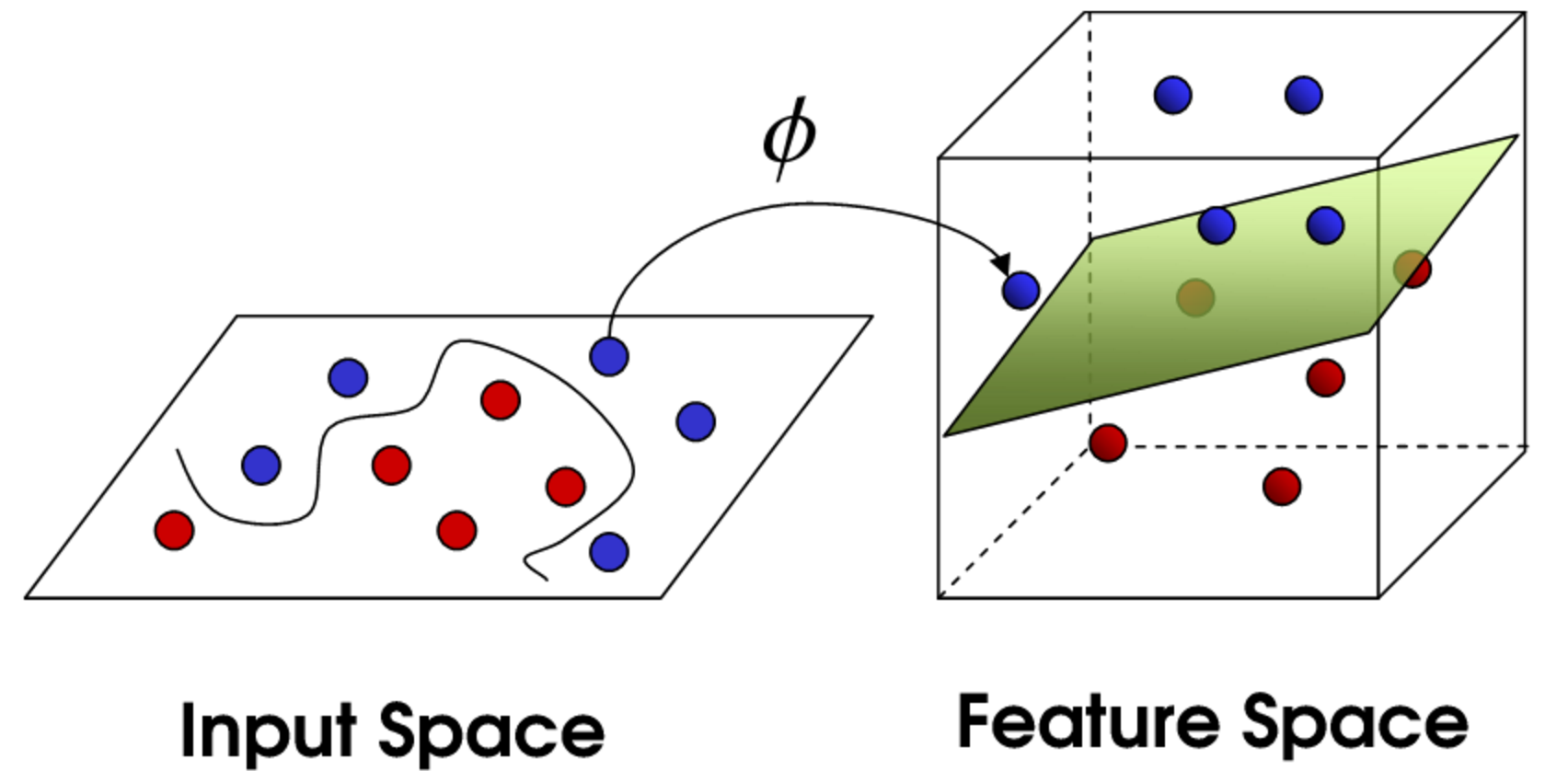
こうしてマージン最大となる分離面を得られたら、未知のデータが入力されたら、写像した時のルールに沿って特徴空間に写像し、特徴空間上で分離面のどこに属するかでクラス判別する。
これがとても分かりやすい。→カーネルトリック参考動画
データ用意
irisのデータを利用。ここと一緒。
データの概要
{describe_iris.py}
iris.head()
の長さと幅のデータ
やってみる
{svm.py}
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
from sklearn import datasets
from sklearn.cross_validation import train_test_split # クロスバリデーション用
# データ用意
iris = datasets.load_iris() # データロード
X = iris.data # 説明変数セット
Y = iris.target # 目的変数セット
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, random_state=0) # random_stateはseed値。
# SVM実行
from sklearn.svm import SVC # SVM用
model = SVC() # インスタンス生成
model.fit(X_train, Y_train) # SVM実行
# 予測実行
from sklearn import metrics # 精度検証用
predicted = model.predict(X_test) # テストデーテへの予測実行
metrics.accuracy_score(Y_test, predicted)
> 0.97368421052631582
精度97.4%。高い。