目次と前回の記事

実装の進捗状況と前回までのおさらい

〇×ゲームの仕様と進捗状況

正方形で区切られた 3 x 3 の 2 次元のゲーム盤上でゲームを行う
ゲーム開始時には、ゲーム盤のすべてのマスは空になっている
2 人のプレイヤーが遊ぶゲームであり、一人は〇を、もう一人は × のマークを受け持つ
2 人のプレイヤーは、交互に空いている好きなマスに自分のマークを 1 つ置く
先手は〇のプレイヤーである
プレイヤーがマークを置いた結果、縦、横、斜めのいずれかの一直線の 3 マスに同じマークが並んだ場合、そのマークのプレイヤーの勝利とし、ゲームが終了する
すべてのマスが埋まった時にゲームの決着がついていない場合は引き分けとする

仕様の進捗状況は、以下のように表記します。

実装が完了した部分を 背景が灰色の長方形 で記述する
実装の一部が完了した部分を、太字で記述する

これまでに作成したモジュール

以下のリンクから、これまでに作成したモジュールを見ることができます。

前回までのおさらい

前回の記事では、judge メソッドのテストの作業を完了し、judge メソッドにあった 3 つのバグをすべて修正しました。これにより、〇×ゲームの 7 つの仕様 の実装がすべて完了しました。

`judge` メソッドの改良

下記のプログラムは、前回の記事までで実装した judge メソッドです。このプログラムは、かなり長い プログラムになっていますが、判定したいこと を、そのまま記述 しているという点で、or、and、not 演算子 の使い方を 学べば、初心者 でも 自力で記述できる のではないかと思います。

    def judge(self):      
        # 〇 の勝利の判定
        if self.board[0][0] == self.board[1][0] == self.board[2][0] == Marubatsu.CIRCLE or \
            self.board[0][1] == self.board[1][1] == self.board[2][1] == Marubatsu.CIRCLE or \
            self.board[0][2] == self.board[1][2] == self.board[2][2] == Marubatsu.CIRCLE or \
            self.board[0][0] == self.board[0][1] == self.board[0][2] == Marubatsu.CIRCLE or \
            self.board[1][0] == self.board[1][1] == self.board[1][2] == Marubatsu.CIRCLE or \
            self.board[2][0] == self.board[2][1] == self.board[2][2] == Marubatsu.CIRCLE or \
            self.board[0][0] == self.board[1][1] == self.board[2][2] == Marubatsu.CIRCLE or \
            self.board[2][0] == self.board[1][1] == self.board[0][2] == Marubatsu.CIRCLE:
            return Marubatsu.CIRCLE
        # × の勝利の判定
        elif self.board[0][0] == self.board[1][0] == self.board[2][0] == Marubatsu.CROSS or \
            self.board[0][1] == self.board[1][1] == self.board[2][1] == Marubatsu.CROSS or \
            self.board[0][2] == self.board[1][2] == self.board[2][2] == Marubatsu.CROSS or \
            self.board[0][0] == self.board[0][1] == self.board[0][2] == Marubatsu.CROSS or \
            self.board[1][0] == self.board[1][1] == self.board[1][2] == Marubatsu.CROSS or \
            self.board[2][0] == self.board[2][1] == self.board[2][2] == Marubatsu.CROSS or \
            self.board[0][0] == self.board[1][1] == self.board[2][2] == Marubatsu.CROSS or \
            self.board[2][0] == self.board[1][1] == self.board[0][2] == Marubatsu.CROSS:
            return Marubatsu.CROSS     
        # 引き分けの判定
        elif not(self.board[0][0] == Marubatsu.EMPTY or \
            self.board[1][0] == Marubatsu.EMPTY or \
            self.board[2][0] == Marubatsu.EMPTY or \
            self.board[0][1] == Marubatsu.EMPTY or \
            self.board[1][1] == Marubatsu.EMPTY or \
            self.board[2][1] == Marubatsu.EMPTY or \
            self.board[0][2] == Marubatsu.EMPTY or \
            self.board[1][2] == Marubatsu.EMPTY or \
            self.board[2][2] == Marubatsu.EMPTY):
            return Marubatsu.DRAW
        # 上記のどれでもなければ決着がついていない
        else:
            return Marubatsu.PLAYING

正しく動作 するプログラムを記述することが できなければ、そもそも 先に進む ことは 不可能 なので、例え 効率が悪くとも、最初は上記のようなプログラムでも 構わない と思います。

ただし、上記のようなプログラムには、入力ミス がつきもので、たった一つ のデータの 入力を間違っただけ で バグが発生 してしまうという問題があります。また、〇の勝利と × の勝利の判定で 同じような処理 を 2 度記述 しているため、効率が悪い などの問題があります。

そこで、今回と次回の記事では、judge メソッドを様々なアルゴリズムで記述する方法について紹介します。

勝利判定を行うメソッドの定義

まず、judge メソッドの中で、〇の勝利の判定 と、× の勝利の判定 を行う if 文の 条件式 を 見比べて、どの部分 が 異なっている かを確認してください。

よく見ると、Marubatsu.CIRCLE と Marubatsu.CROSS の部分が 異なる だけで、それ以外 の部分は 全く同じ であることがわかるはずです。このような場合は、〇の勝利の判定と、× の勝利の判定を 一つのメソッド で まとめる ことができます。

具体的には、以下のようなメソッドを定義します。

処理：実引数で指定 した プレイヤーが勝利 しているかどうかを判定する
名前：指定したプレイヤーが 勝利者である(is winner) ことを判定するので、is_winner とする
入力：player という仮引数で、判定するプレイヤー の情報を 受け取る
出力：player のプレイヤーが勝利していた場合は True を、そうでなければ False を返す

このメソッドは、以下のプログラムのように定義することができます。なお、具体的な条件式の記述はこの後で行います。

def is_winner(self, player):
    if player が勝利していることを判定する条件式:
        return True
    else:
        return False

この関数を使って、judge メソッド を以下のプログラムのように修正することができます。

from marubatsu import Marubatsu

def judge(self):      
    # 〇 の勝利の判定
    if self.is_winner(Marubatsu.CIRCLE):
        return Marubatsu.CIRCLE
    # × の勝利の判定
    elif self.is_winner(Marubatsu.CROSS):
        return Marubatsu.CROSS
    # 引き分けの判定
    elif not(self.board[0][0] == Marubatsu.EMPTY or \
        self.board[1][0] == Marubatsu.EMPTY or \
        self.board[2][0] == Marubatsu.EMPTY or \
        self.board[0][1] == Marubatsu.EMPTY or \
        self.board[1][1] == Marubatsu.EMPTY or \
        self.board[2][1] == Marubatsu.EMPTY or \
        self.board[0][2] == Marubatsu.EMPTY or \
        self.board[1][2] == Marubatsu.EMPTY or \
        self.board[2][2] == Marubatsu.EMPTY):
        return Marubatsu.DRAW
    # 上記のどれでもなければ決着がついていない
    else:
        return Marubatsu.PLAYING 
    
Marubatsu.judge = judge

修正箇所

from marubatsu import Marubatsu

def judge(self):      
    # 〇 の勝利の判定
-   if self.board[0][0] == self.board[1][0] == self.board[2][0] == Marubatsu.CIRCLE or \
-      self.board[0][1] == self.board[1][1] == self.board[2][1] == Marubatsu.CIRCLE or \
-      self.board[0][2] == self.board[1][2] == self.board[2][2] == Marubatsu.CIRCLE or \
-      self.board[0][0] == self.board[0][1] == self.board[0][2] == Marubatsu.CIRCLE or \
-      self.board[1][0] == self.board[1][1] == self.board[1][2] == Marubatsu.CIRCLE or \
-      self.board[2][0] == self.board[2][1] == self.board[2][2] == Marubatsu.CIRCLE or \
-      self.board[0][0] == self.board[1][1] == self.board[2][2] == Marubatsu.CIRCLE or \
-      self.board[2][0] == self.board[1][1] == self.board[0][2] == Marubatsu.CIRCLE:
+   if self.is_winner(Marubatsu.CIRCLE):
        return Marubatsu.CIRCLE
    # × の勝利の判定
-   elif self.board[0][0] == self.board[1][0] == self.board[2][0] == Marubatsu.CROSS or \
-        self.board[0][1] == self.board[1][1] == self.board[2][1] == Marubatsu.CROSS or \
-        self.board[0][2] == self.board[1][2] == self.board[2][2] == Marubatsu.CROSS or \
-        self.board[0][0] == self.board[0][1] == self.board[0][2] == Marubatsu.CROSS or \
-        self.board[1][0] == self.board[1][1] == self.board[1][2] == Marubatsu.CROSS or \
-        self.board[2][0] == self.board[2][1] == self.board[2][2] == Marubatsu.CROSS or \
-        self.board[0][0] == self.board[1][1] == self.board[2][2] == Marubatsu.CROSS or \
-        self.board[2][0] == self.board[1][1] == self.board[0][2] == Marubatsu.CROSS:
+   elif self.is_winner(Marubatsu.CROSS):
        return Marubatsu.CROSS
    # 引き分けの判定
    elif not(self.board[0][0] == Marubatsu.EMPTY or \
        self.board[1][0] == Marubatsu.EMPTY or \
        self.board[2][0] == Marubatsu.EMPTY or \
        self.board[0][1] == Marubatsu.EMPTY or \
        self.board[1][1] == Marubatsu.EMPTY or \
        self.board[2][1] == Marubatsu.EMPTY or \
        self.board[0][2] == Marubatsu.EMPTY or \
        self.board[1][2] == Marubatsu.EMPTY or \
        self.board[2][2] == Marubatsu.EMPTY):
        return Marubatsu.DRAW
    # 上記のどれでもなければ決着がついていない
    else:
        return Marubatsu.PLAYING 
    
Marubatsu.judge = judge

この修正によって、下記のような利点が得られます。

元の judge メソッド の〇の勝利の判定と × の勝利の判定を行う、一見すると何を行っているかが わかりづらい複雑な条件式 が、is_winner という、その 名前から 何を行っているかが わかりやすい メソッドの呼び出しに 置き換えられている ので、judge メソッドで行われる処理の 見た目 が わかりやすくなる。このような、具体的な処理の記述 を、メソッドの名前などの、短く わかりやすい 記述 置き換える ことを、抽象化 と呼ぶ
同じような処理 を行う〇の勝利の判定と、× の勝利の判定を行う条件式が、is_winner の中の 1 箇所 に まとめられる ので、プログラムの 記述が短く なる
1 箇所 に まとめる ことで、間違っていた場合 の修正や、条件式の改良 を行う際に、その 1 箇所だけ を修正すれば済むようになる

`is_winner` の実装

次に、is_winner の 条件式を記述 します。player が勝利 しているかどうかを判定する 条件式 は、下記のプログラムのように、judge メソッドに記述されていた、〇の勝利の判定 を行う 条件式 の Marubatsu.CIRCLE を player に 置き換える ことで記述することができます。

元の judge メソッド では、〇が勝利した場合 に行う処理は、return Marubatsu.CIRCLE でしたが、is_winner では、player が勝利した場合 は True を返す ので return True を記述 する必要がある点に注意して下さい。また、player が勝利 していない 場合は、False を返します。

def is_winner(self, player):
    # player が勝利しているかどうかを判定する
    if self.board[0][0] == self.board[1][0] == self.board[2][0] == player or \
       self.board[0][1] == self.board[1][1] == self.board[2][1] == player or \
       self.board[0][2] == self.board[1][2] == self.board[2][2] == player or \
       self.board[0][0] == self.board[0][1] == self.board[0][2] == player or \
       self.board[1][0] == self.board[1][1] == self.board[1][2] == player or \
       self.board[2][0] == self.board[2][1] == self.board[2][2] == player or \
       self.board[0][0] == self.board[1][1] == self.board[2][2] == player or \
       self.board[2][0] == self.board[1][1] == self.board[0][2] == player:
        return True
    else:
        return False

Marubatsu.is_winner = is_winner

修正箇所（judge メソッドの〇の勝利を判定する if 文との比較です)

-   if self.board[0][0] == self.board[1][0] == self.board[2][0] == Marubatsu.CIRCLE or \
+   if self.board[0][0] == self.board[1][0] == self.board[2][0] == player or \
-      self.board[0][1] == self.board[1][1] == self.board[2][1] == Marubatsu.CIRCLE or \
+      self.board[0][1] == self.board[1][1] == self.board[2][1] == player or \
-      self.board[0][2] == self.board[1][2] == self.board[2][2] == Marubatsu.CIRCLE or \
+      self.board[0][2] == self.board[1][2] == self.board[2][2] == player or \
-      self.board[0][0] == self.board[0][1] == self.board[0][2] == Marubatsu.CIRCLE or \
+      self.board[0][0] == self.board[0][1] == self.board[0][2] == player or \
-      self.board[1][0] == self.board[1][1] == self.board[1][2] == Marubatsu.CIRCLE or \
+      self.board[1][0] == self.board[1][1] == self.board[1][2] == player or \
-      self.board[2][0] == self.board[2][1] == self.board[2][2] == Marubatsu.CIRCLE or \
+      self.board[2][0] == self.board[2][1] == self.board[2][2] == player or \
-      self.board[0][0] == self.board[1][1] == self.board[2][2] == Marubatsu.CIRCLE or \
+      self.board[0][0] == self.board[1][1] == self.board[2][2] == player or \
-      self.board[2][0] == self.board[1][1] == self.board[0][2] == Marubatsu.CIRCLE:
+      self.board[2][0] == self.board[1][1] == self.board[0][2] == player:
-       return Marubatsu.CIRCLE
+       return True
+   else:
+       return False

修正した `judge` メソッドのテスト

judge メソッドを修正したので、テスト を行う必要があります。今回の修正では、is_winner という 新しい関数を定義 したので、厳密なテスト を行うのであれば、is_winner に対する テスト を行う必要があるので大変だと思う人がいるかもしれません。

関数やメソッドを修正 した結果、関数の中の 処理の流れ が大きく 変わったり、新しい関数を定義 する事はよくあることですが、そのたびに、新しい 処理の流れに対応した テストケースを作成 したり、新しい関数 に対する テストを行う のは大変で、現実的に無理 なことが多いでしょう。

今回のように、judge メソッドに 新しい機能 を付け 加える の ではなく、judge メソッドの機能そのものは 全く変化しない ような修正を行った場合は、それまでに行ったテスト を そのまま流用 するのが 一般的 です。しっかりとしたテスト が行えていれば、処理の流れが変わったり、新しい関数を定義していても、十分な精度 で テストを行う ことが できる からです。

そこで、本記事でも、今後は修正した judge メソッド の テスト は、前回までの記事 で作成した test_judge を そのまま使って行う ことにします。ただし、前回の記事で作成した test_judge は、実引数 に テストケースを記述 する必要がある点が不便です。そこで、test_judge を 実引数を記述せず に呼び出した場合は、前回の記事で作成した、MC/DC と 簡易的な組み合わせ網羅 を 組み合わせたテストケース で テストを行う ように修正します。

下記は、そのように test_judge を修正したプログラムです。修正点は以下の通りです。

testcases を デフォルト引数値 が None に設定された デフォルト引数 にする
関数のブロックの最初に、testcases が None の場合 に、testcases に MC/DC と簡易的な組み合わせ網羅を組み合わせた テストケースのデータを代入 する

testcases に対応 する 実引数を記述せず に test_judge を 呼び出す と、仮引数 testcases にデフォルト値である None が代入 された状態で、test_judge のブロックが実行されます。その結果、最初の if 文 によって、testcases に MC/DC と簡易的な組み合わせ網羅を組み合わせた テストケースのデータ が代入されます。以前の記事で説明したように、None であるか どうかの判定は、== ではなく、is 演算子 で行う必要がある点に注意して下さい。

def test_judge(testcases=None, debug=False):
    if testcases is None:
        testcases = {
            # 決着がついていない場合のテストケース
            Marubatsu.PLAYING: [
                # ゲーム盤に一つもマークが配置されていない場合のテストケース
                "",
                # 一つだけマークが配置されていない場合のテストケース
                "C3,A2,B1,B2,C2,C1,A3,B3",
                "A1,A2,C3,B2,C2,C1,A3,B3",
                "A1,A2,B1,B2,C2,C3,A3,B3",
                "A1,C3,B1,B2,C2,C1,A3,B3",
                "A1,A2,B1,C3,C2,C1,A3,B3",
                "A1,A2,B1,B2,C3,C1,A3,B3",
                "A1,A2,B1,B2,C2,C1,C3,B3",
                "A1,A2,B1,B2,A3,C1,C2,C3",
                "A1,A2,B1,B2,C2,C1,A3,B3",
            ],   
            # 〇の勝利のテストケース
            Marubatsu.CIRCLE: [
                "A1,A2,B1,B2,C1",
                "A2,A1,B2,B1,C2",
                "A3,A1,B3,B1,C3",
                "A1,B1,A2,B2,A3",
                "B1,A1,B2,A2,B3",
                "C1,A1,C2,A2,C3",
                "A1,A2,B2,A3,C3",
                "A3,A1,B2,A2,C1",
                # 簡易的な組み合わせ網羅の 6 のテストケース
                "A1,B1,A2,B2,B3,C1,C3,C2,A3", 
            ],
            # × の勝利のテストケース
            Marubatsu.CROSS: [
                "A2,A1,B2,B1,A3,C1",
                "A1,A2,B1,B2,A3,C2",
                "A1,A3,B1,B3,A2,C3",
                "B1,A1,B2,A2,C1,A3",
                "A1,B1,A2,B2,C1,B3",
                "A1,C1,A2,C2,B1,C3",
                "A2,A1,A3,B2,B1,C3",
                "A1,C1,B1,B2,A2,A3",
            ],
            # 引き分けの場合のテストケース
            Marubatsu.DRAW: [
                "A1,A2,B1,B2,C2,C1,A3,B3,C3",
            ], 
        }

    print("Start")
    以下同じなので略

下記のプログラムを実行することで、修正した judge のテストを行うことができます。実行結果から、すべてのテストケースで期待された処理が行われることが確認できます。

test_judge()

実行結果

Start
test winner = playing
oooooooooo
test winner = o
ooooooooo
test winner = x
oooooooo
test winner = draw
o
Finished

`is_winner` の微修正

先程実装した、is_winner のように、条件式 が True の場合は、True を、そうでない場合 は False を返す 関数は、条件式の 計算結果そのもの が、返り値に等しい ので、下記のプログラムのように、if 文を使わず に、条件式 の計算結果を 直接返す ように修正することができます。

def is_winner(self, player):
    # player が勝利していることを表す条件式の計算結果を返す
    return self.board[0][0] == self.board[1][0] == self.board[2][0] == player or \
           self.board[0][1] == self.board[1][1] == self.board[2][1] == player or \
           self.board[0][2] == self.board[1][2] == self.board[2][2] == player or \
           self.board[0][0] == self.board[0][1] == self.board[0][2] == player or \
           self.board[1][0] == self.board[1][1] == self.board[1][2] == player or \
           self.board[2][0] == self.board[2][1] == self.board[2][2] == player or \
           self.board[0][0] == self.board[1][1] == self.board[2][2] == player or \
           self.board[2][0] == self.board[1][1] == self.board[0][2] == player

Marubatsu.is_winner = is_winner

下記のプログラムを実行することで、修正した judge メソッドで、すべてのテストケースで期待された処理が行われることが確認できます。実行結果は先程と同じなので省略します。

test_judge()

`is_winner` のアルゴリズムその 1 （`+` 演算子を使う）

勝利判定 を行う is_winner を実装したので、今回の記事で紹介する、さまざまな 勝利判定の アルゴリズム は、is_winner を修正 することで実装することにします。

is_winner の 条件式 の中では、一直線上に 3 つ並んだマス に配置された マーク が winner と等しい かどうかを、下記のプログラムのように、== 演算子 を連結して記述しました。

self.board[0][0] == self.board[1][0] == self.board[2][0] == player

以前の記事で説明したように、このような記述は、Python 以外 の 多くのプログラム言語 では 行うことができず¹、下記のように、and 演算子 を使って 記述する必要 があり（長いので途中で改行しました）、その場合は 記述が長く なってしまいます。

self.board[0][0] == self.board[1][0] and self.board[1][0] == self.board[2][0] and \
self.board[2][0] == player

+ 演算子 を使って、文字列を結合 することができるプログラム言語²であれば、上記の判定を行う 条件式 を、別のアルゴリズム で記述することができるので、その方法を紹介します。

例えば、〇が (0, 0)、(1, 0)、(2, 0) の 3 つのマスに 並んでいる 場合、self.board[0][0] と self.board[1][0] と self.board[2][0] には、Marubatsu.CIRCLE に代入された "o" という文字列が代入されています。従って、この 3 つ を + 演算子で結合 すると、Marubatsu.CIRCLE + Marubatsu.CIRCLE + Marubatsu.CIRCLE、すなわち "ooo" という 文字列が代入 されているはずです。また、Marubatsu.CIRCLE を 3 つ結合 した文字列は、Marubatsu.CIRCLE * 3 と記述できます。

上記の事から、player のマーク が (0, 0)、(1, 0)、(2, 0) の 3 つのマスに 並んでいる ことを判定する 条件式 は、下記のプログラムのように記述することができます。

self.board[0][0] + self.board[1][0] + self.board[2][0] == player * 3

下記は、この方法で is_winner を修正したプログラムです。

def is_winner(self, player):
    # player が勝利していることを表す条件式の計算結果を返す
    return self.board[0][0] + self.board[1][0] + self.board[2][0] == player * 3 or \
           self.board[0][1] + self.board[1][1] + self.board[2][1] == player * 3 or \
           self.board[0][2] + self.board[1][2] + self.board[2][2] == player * 3 or \
           self.board[0][0] + self.board[0][1] + self.board[0][2] == player * 3 or \
           self.board[1][0] + self.board[1][1] + self.board[1][2] == player * 3 or \
           self.board[2][0] + self.board[2][1] + self.board[2][2] == player * 3 or \
           self.board[0][0] + self.board[1][1] + self.board[2][2] == player * 3 or \
           self.board[2][0] + self.board[1][1] + self.board[0][2] == player * 3

Marubatsu.is_winner = is_winner

修正箇所

def is_winner(self, player):
    # player が勝利していることを表す条件式の計算結果を返す
-   return self.board[0][0] == self.board[1][0] == self.board[2][0] == player or \
+   return self.board[0][0] + self.board[1][0] + self.board[2][0] == player * 3 or \
-          self.board[0][1] == self.board[1][1] == self.board[2][1] == player or \
+          self.board[0][1] + self.board[1][1] + self.board[2][1] == player * 3 or \
-          self.board[0][2] == self.board[1][2] == self.board[2][2] == player or \
+          self.board[0][2] + self.board[1][2] + self.board[2][2] == player * 3 or \
-          self.board[0][0] == self.board[0][1] == self.board[0][2] == player or \
+          self.board[0][0] + self.board[0][1] + self.board[0][2] == player * 3 or \
-          self.board[1][0] == self.board[1][1] == self.board[1][2] == player or \
+          self.board[1][0] + self.board[1][1] + self.board[1][2] == player * 3 or \
-          self.board[2][0] == self.board[2][1] == self.board[2][2] == player or \
+          self.board[2][0] + self.board[2][1] + self.board[2][2] == player * 3 or \
-          self.board[0][0] == self.board[1][1] == self.board[2][2] == player or \
+          self.board[0][0] + self.board[1][1] + self.board[2][2] == player * 3 or \
-          self.board[2][0] == self.board[1][1] == self.board[0][2] == player
+          self.board[2][0] + self.board[1][1] + self.board[0][2] == player * 3

test_judge()

条件式の中に player * 3 を何度も記述するのは効率が悪いので、下記のプログラムのように、先に player * 3 の計算結果を変数に代入するという方法もあります。

def is_winner(self, player):
    wintext = player * 3
    # player が勝利していることを表す条件式の計算結果を返す
    return self.board[0][0] + self.board[1][0] + self.board[2][0] == wintext or \
           self.board[0][1] + self.board[1][1] + self.board[2][1] == wintext or \
           self.board[0][2] + self.board[1][2] + self.board[2][2] == wintext or \
           self.board[0][0] + self.board[0][1] + self.board[0][2] == wintext or \
           self.board[1][0] + self.board[1][1] + self.board[1][2] == wintext or \
           self.board[2][0] + self.board[2][1] + self.board[2][2] == wintext or \
           self.board[0][0] + self.board[1][1] + self.board[2][2] == wintext or \
           self.board[2][0] + self.board[1][1] + self.board[0][2] == wintext

Marubatsu.is_winner = is_winner

修正箇所

def is_winner(self, player):
+   wintext = player * 3
    # player が勝利していることを表す条件式の計算結果を返す
-   return self.board[0][0] + self.board[1][0] + self.board[2][0] == player * 3 or \
+   return self.board[0][0] + self.board[1][0] + self.board[2][0] == wintext or \
-          self.board[0][1] + self.board[1][1] + self.board[2][1] == player * 3 or \
+          self.board[0][1] + self.board[1][1] + self.board[2][1] == wintext or \
-          self.board[0][2] + self.board[1][2] + self.board[2][2] == player * 3 or \
+          self.board[0][2] + self.board[1][2] + self.board[2][2] == wintext or \
-          self.board[0][0] + self.board[0][1] + self.board[0][2] == player * 3 or \
+          self.board[0][0] + self.board[0][1] + self.board[0][2] == wintext or \
-          self.board[1][0] + self.board[1][1] + self.board[1][2] == player * 3 or \
+          self.board[1][0] + self.board[1][1] + self.board[1][2] == wintext or \
-          self.board[2][0] + self.board[2][1] + self.board[2][2] == player * 3 or \
+          self.board[2][0] + self.board[2][1] + self.board[2][2] == wintext or \
-          self.board[0][0] + self.board[1][1] + self.board[2][2] == player * 3 or \
+          self.board[0][0] + self.board[1][1] + self.board[2][2] == wintext or \
-          self.board[2][0] + self.board[1][1] + self.board[0][2] == player * 3
+          self.board[2][0] + self.board[1][1] + self.board[0][2] == wintext
           
Marubatsu.is_winner = is_winner

`is_winner` のアルゴリズムその 2 （データの分離と繰り返し処理）

is_winner では、条件式の中 に、マスの座標 を表すデータを 直接記述 していますが、test_judge の中で着手を行うための 座標データ を、test_judge の中の着手を行うプログラムから分離したように、is_winner においても、マスの座標を表す データ を分離する方法が考えられます。

条件式からのデータの分離

条件式 の中から データ を分離するためには、どのような データ が条件式に記述されているかを 考える 必要があります。下記は、is_winner の中の条件式の最初の行を抜粋したものですが、この中の データ は、self.board の インデックス である 0、0、1、0、2、0 の 6 つ です。

self.board[0][0] == self.board[1][0] == self.board[2][0] == player

この 6 つのデータを list で表現 すると、下記のようになります

[ 0, 0, 1, 0, 2, 0 ]

下記のプログラムは、このデータ を 使って 上記の 条件式を記述 したものです。1 行目は、以前の記事で説明した、反復可能オブジェクトの展開を使って、6 つ の list の要素を、6 つの変数 に代入しています。2 行目では、その 変数を使って 条件式を修正しています。

x1, y1, x2, y2, x3, y3 = [ 0, 0, 1, 0, 2, 0 ]
self.board[x1][y1] == self.board[x2][y2] == self.board[x3][y3] == player

6 つのデータは、3 組 の座標を表すデータなので、下記のように、座標を表す 2 つのデータを list で表現 することで、全体を 2 次元配列 を表す list で表現 することもできます。

[ [0, 0], [1, 0], [2, 0] ]

2 次元以上 配列を表すの list の要素 を展開によって 個別の変数 に代入する場合は、下記のプログラムのように、代入文の 右辺の list と 同じ構造 で代入文の 左辺を記述 します。代入文の 左辺の中 に記述された変数に、対応する 右辺の要素の値 が代入されます。

[[x1, y1], [x2, y2], [x3, y3]] = [[0, 0], [1, 0], [2, 0]]

元の条件式 には、このようなデータが 8 つ あるので、それを list で表現 すると、下記のプログラムのような 2 次元配列 を表す list になります。このデータは、勝利の判定（judge）を行うための座標（coordinates）の リスト（list）なので、judge_coords_list という 変数に代入 します。

judge_coords_list = [
    [ 0, 0, 1, 0, 2, 0 ],
    [ 0, 1, 1, 1, 2, 1 ],
    [ 0, 2, 1, 2, 2, 2 ],
    [ 0, 0, 0, 1, 0, 2 ],
    [ 1, 0, 1, 1, 1, 2 ],
    [ 2, 0, 2, 1, 2, 2 ],
    [ 0, 0, 1, 1, 2, 2 ],
    [ 2, 0, 1, 1, 0, 2 ],
]

for 文を使った `is_winner` の記述

このデータを使って、is_winner を下記プログラムのように for 文 を使って記述できます。

1 行目の for 文は、上記のデータを 順番に取り出し て x1 ~ y3 の 6 つの変数に代入 し、2、3 行目の for 文のブロックの処理を実行するという 繰り返し処理 を行います。

2 行目は、取り出したすべてのマス に、player の マークが並んでいるか どうかを判定します。

for x1, y1, x2, y2, x3, y3 in judge_coords_list:
    if self.board[x1][y1] == self.board[x2][y2] == self.board[x3][y3] == player:
        return True

return False

〇×ゲームでは、8 種類ある いずれか の 1 直線上に 同じマークが並べば、その時点で そのマークのプレイヤーの 勝利が決まります。従って、8 種類を調べる途中で player の 勝利が決まった場合 は、残りを調べる 必要は ありません。return 文 を実行すると、関数の ブロックの処理 が その時点で終了 するので、3 行目に return True を記述 することで、1 行目の for 文の 繰り返し処理 の途中であっても、player の勝利と判定 した時点で残りの 繰り返し処理 は 行われません。

player のマークが一直線上に 配置されている 場合は、3 行目の return 文 によって 関数の処理が終了 するので、for 文の 繰り返し処理 が 終了する ことは ありません。

逆に、player のマークが 一直線上 に 配置されていない 場合は、1 ~ 3 行目の for 文の 繰り返しの処理 で、2 行目の条件式 が True になる ことは ありません。そのような場合は、3 行目の return 文 が実行されることは無いので、for 文の 繰り返し が 必ず終了 します。

このことから、for 文の繰り返し処理の後 に記述された処理は、player が 勝利していない 場合 のみ実行 されます。従って、player が 勝利していない ことを表す return False を for 文の繰り返し処理の後 の 5 行目に記述しています。

下図は、このプログラムのフローチャートです。

is_winner の微修正 の場合と同様に、2、3 行目 を下記のプログラムのように記述すれば良いと思う人がいるかもしれませんが、そのように記述すると バグが発生 します。

for x1, y1, x2, y2, x3, y3 in judge_coords_list:
    return self.board[x1][y1] == self.board[x2][y2] == self.board[x3][y3] == player

修正箇所

for x1, y1, x2, y2, x3, y3 in judge_coords_list:
-   if self.board[x1][y1] == self.board[x2][y2] == self.board[x3][y3] == player:
-       return True
+   return self.board[x1][y1] == self.board[x2][y2] == self.board[x3][y3] == player

バグの原因は、上記のように記述すると、1 行目の for 文 の最初の 繰り返し処理 で、必ず return 文が実行 されるため、2 つ目以降 の 繰り返し処理 が決して 行われない からです。

例えば、ゲーム盤の 一番上の行以外 で player のマークが 一直線上に配置 されていた場合、最初の for 文の 繰り返し で (0, 0)、(1, 0)、(2, 0) のマスに player のマークが 配置されていない ため、その時点 で False が返され てしまいます。

下記のプログラムが、修正後の is_winner です。

def is_winner(self, player):
    # 一直線上のマスの座標を表すデータを集めた list
    judge_coords_list = [
        [ 0, 0, 1, 0, 2, 0 ],
        [ 0, 1, 1, 1, 2, 1 ],
        [ 0, 2, 1, 2, 2, 2 ],
        [ 0, 0, 0, 1, 0, 2 ],
        [ 1, 0, 1, 1, 1, 2 ],
        [ 2, 0, 2, 1, 2, 2 ],
        [ 0, 0, 1, 1, 2, 2 ],
        [ 2, 0, 1, 1, 0, 2 ],
    ]

    # 一直線上のマスの座標を順番に取り出す繰り返し処理
    for x1, y1, x2, y2, x3, y3 in judge_coords_list:
        # 取り出した一直線上のマスに player が配置されているかどうかを判定する
        if self.board[x1][y1] == self.board[x2][y2] == self.board[x3][y3] == player:
            # 並んでいれば player の勝利なので True を返す
            return True

    # どの一直線上にも配置されていない場合は、player は勝利していないので False を返す
    return False

Marubatsu.is_winner = is_winner

test_judge()

修正前 のプログラムでは、self.board[0][0] のように、self.board のような座標データ以外の記述と、座標データ の記述が混在していますが、修正後 のプログラムでは、座標データ が 一か所 に まとめられている ので、座標データ を記述、修正する際に、座標データ の事だけに集中して 効率よく プログラムを記述することができます。

`is_winner` のアルゴリズムその 3 （繰り返しを使った一直線上の並びの判定）

これまでの is_winner の 条件式 には、その中 に 3 つの 一直線上のマス を表す self.board の要素 を 直接記述 していました。〇×ゲームのように、一直線上のマスの数が 3 つしかない 場合は、そのような条件式を記述するのはそれほど 大変ではありません が、例えばもっと 大きなゲーム盤 のゲームで、一直線上のマスの数が 9 つの場合に、その一直線上に同じマークが並ぶことを判定する 条件式 は、下記のように self.board の要素を 9 つも記述 する必要があるため、記述が大変 です。

self.board[x1][y1] == self.board[x2][y2] == self.board[x3][y3] == \
self.board[x4][y4] == self.board[x5][y5] == self.board[x6][y6] == \
self.board[x7][y7] == self.board[x8][y8] == self.board[x9][y9] == player

他にも、元の条件式では、4 * 4 の〇×ゲームのような、3 つ以外 の一直線上のマスに同じマークが並んだ場合を判定することが できない という欠点があります。

このような欠点を解消する方法として、特定の数 の一直線上のマスに 同じマークが配置 されていることを、for 文による 繰り返し処理 で判定するというアルゴリズムがあります。

アルゴリズムの説明

具体的には以下のようなアルゴリズムで判定を行います。

一直線上のマスの座標を 順番に取り出す
取り出した座標のマス に、player のマークが 配置されているかどうか を 調べる
配置されていなければ 一直線上に 並んでいない ことが確定し、処理を終了 する
まだ マスが残っていれば 手順 1 へ戻る
一直線上 のマスに player のマークが配置されていることが確定する

この処理 を、is_winner の中に記述しても構いませんが、関数で定義 したほうがプログラムが わかりやすく なったり、この処理 をプログラムの 様々な場所から利用 できるようになるので、関数で定義する事にします。

具体的には、以下のようなメソッドを定義します。

処理：実引数 で指定した すべてのマスに、実引数 で指定した マークが配置 されているかどうかを 調べる
名前：指定したマスに同じ（same）マークが配置されているかを判定するので、is_same とする
入力：仮引数 coords で マスの座標の list を、仮引数 mark で マークの情報 を受け取る
出力：corrds で指定された すべてのマス に mark のマークが 配置されている場合 は True を、そうでなければ False を返す

coords には、一直線上 に並んだ マスの座標 を代入する必要があるので、例えば (0, 0)、(1, 0)、(2, 0) の場合は [[0, 0], [1, 0], [2, 0]] という 2 次元配列の list を代入することにします。

`is_same` の実装

is_same は、先程のアルゴリズムを使って下記のプログラムのように定義することができます。

1  def is_same(self, coords, mark):
2      for x, y in coords:
3          if self.board[x][y] != mark:
4              return False
5
6      return True
7
8  Marubatsu.is_same = is_same

行番号のないプログラム

def is_same(self, coords, mark):
    for x, y in coords:
        if self.board[x][y] != mark:
            return False
    return True

Marubatsu.is_same = is_same

2 行目の for 文で、coords の先頭の要素から 順番に座標を取り出し、x と y に代入するという 繰り返し処理 を行います。

3 行目では、(x, y) のマスに mark のマークが 配置されているか どうかを判定し、配置されていなければ、coords が指定する 一直線上 に 配置されていない ことが確定するので 4 行目の return 文 によって False を返し、関数の処理を終了 します。

mark のマークが一直線上に 配置されていない 場合は、必ず 4 行目の return 文が実行 されるので、for 文 の繰り返し処理の 後で記述 された処理が 実行される ことは決して ありません。

逆に、mark のマークが 一直線上 に 配置されている 場合は、2 ~ 4 行目の for 文の 繰り返しの処理 で、3 行目の条件式 が True になる ことは ありません。そのような場合は、4 行目の return 文 が実行されることは無いので、for 文の 繰り返し が 必ず終了 します。

このことから、for 文の繰り返し処理の後 に記述された処理は、mark のマークが一直線上に 配置されている 場合 のみ実行 されます。従って、mark のマークが一直線上に 配置されている ことを表す、return True を for 文の繰り返し処理の後 の 6 行目に記述しています。

下図は、このプログラムのフローチャートです。

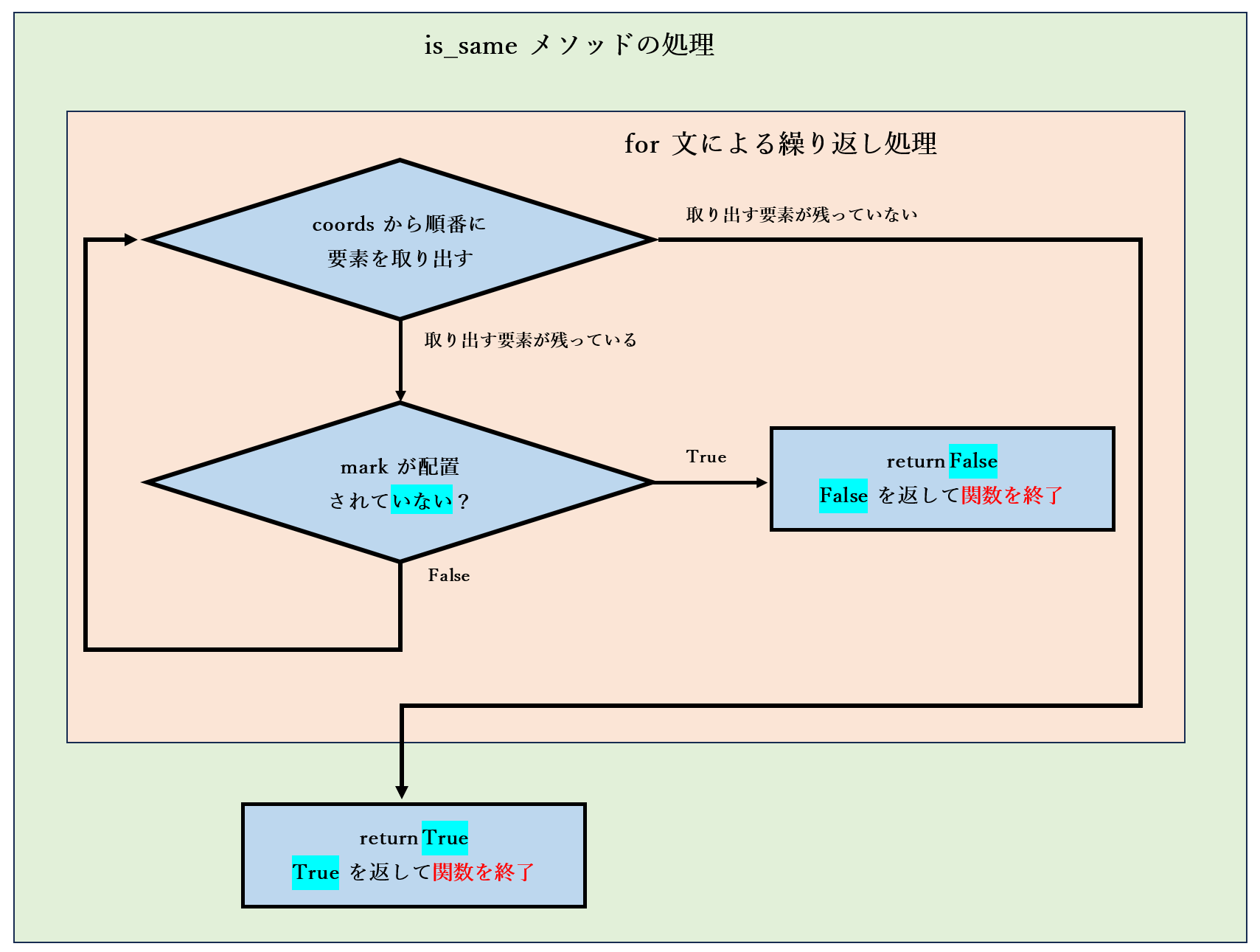
上記の説明と、フローチャートを見て、先程の is_winner のアルゴリズムその 2 で紹介したプログラムに 似ている と思った方が多いのではないかと思いますが、実際に似ています。

その 2 のアルゴリズムは、いずれか一つ の条件が 満たされている ことを、繰り返し処理 で判定するアルゴリズムです。

一方、その 3 のアルゴリズムは その逆 で、すべての条件 が 満たされている ことを 繰り返し処理 で判定するアルゴリズムです。

従って、その 2 とその 3 のプログラムは、if 文の 条件式 の == と !=、return 文 で返す True と False が逆になっている以外は、同じ構造の処理 を行っています。

下記は、その 2 とその 3 のフローチャートを並べたものです。分かりやすいように、その 3 では、その 2 と逆になっている部分の 背景を水色で表記 しましたので、見比べて確認 して下さい。

`is_same` を使った `is_winner` の記述

is_same を使って、is_winner を以下のように記述することができます。その 2 の is_winner から修正した部分は以下の通りです。

judge_coords_list の データ構造 を、is_same の導入に 合わせて修正 した
for 文の中で、judge_coords_list から 取り出したデータ を coords という 一つの変数に代入 するようにした
for 文の中で記述していた if 文の条件式 を、is_same メソッドを使うように修正した

def is_winner(self, player):
    # 一直線上のマスの座標を表すデータを集めた list
    judge_coords_list = [
        [ [0, 0], [1, 0], [2, 0] ],
        [ [0, 1], [1, 1], [2, 1] ],
        [ [0, 2], [1, 2], [2, 2] ],
        [ [0, 0], [0, 1], [0, 2] ],
        [ [1, 0], [1, 1], [1, 2] ],
        [ [2, 0], [2, 1], [2, 2] ],
        [ [0, 0], [1, 1], [2, 2] ],
        [ [2, 0], [1, 1], [0, 2] ],
    ]

    # 一直線上のマスの座標を順番に取り出す繰り返し処理
    for coords in judge_coords_list:
        # 取り出した一直線上のマスに player が配置されているかどうかを判定する
        if self.is_same(coords, player):
            # 並んでいれば player の勝利なので True を返す
            return True

    # どの一直線上にも配置されていない場合は、player は勝利していないので False を返す
    return False

Marubatsu.is_winner = is_winner

修正箇所

def is_winner(self, player):
    # 一直線上のマスの座標を表すデータを集めた list
    judge_coords_list = [
-       [ 0, 0, 1, 0, 2, 0 ],
-       [ 0, 1, 1, 1, 2, 1 ],
-       [ 0, 2, 1, 2, 2, 2 ],
-       [ 0, 0, 0, 1, 0, 2 ],
-       [ 1, 0, 1, 1, 1, 2 ],
-       [ 2, 0, 2, 1, 2, 2 ],
-       [ 0, 0, 1, 1, 2, 2 ],
-       [ 2, 0, 1, 1, 0, 2 ],
+       [ [0, 0], [1, 0], [2, 0] ],
+       [ [0, 1], [1, 1], [2, 1] ],
+       [ [0, 2], [1, 2], [2, 2] ],
+       [ [0, 0], [0, 1], [0, 2] ],
+       [ [1, 0], [1, 1], [1, 2] ],
+       [ [2, 0], [2, 1], [2, 2] ],
+       [ [0, 0], [1, 1], [2, 2] ],
+       [ [2, 0], [1, 1], [0, 2] ],
    ]

    # 一直線上のマスの座標を順番に取り出す繰り返し処理
-   for x1, y1, x2, y2, x3, y3 in judge_coords_list:
+   for coords in judge_coords_list:
        # 取り出した一直線上のマスに player が配置されているかどうかを判定する
-       if self.board[x1][y1] == self.board[x2][y2] == self.board[x3][y3] == player:
+       if self.is_same(coords, player):
            # 並んでいれば player の勝利なので True を返す
            return True

    # どの一直線上にも配置されていない場合は、player は勝利していないので False を返す
    return False

Marubatsu.is_winner = is_winner

test_judge()

実例は示しませんが、この変更により、ゲーム盤のサイズ を 4 * 4 に変更 し、[[0, 0], [1, 0], [2, 0], [3, 0]] のような判定を行うためのデータを用意すれば、3 マス以外 の一直線上に同じマークが並んだ場合に対しても 正しく判定 を行うことが できる ようになります。

judge_coords_list のデータを、__テストケース__で 座標を記述 した場合と同様に、下記のような Excel 座標 で記述することもできます。

    judge_coords_list = [
        "A1,B1,C1",
        "A2,B2,C2",
        "A3,B3,C3",
        "A1,A2,A3",
        "B1,B2,B3",
        "C1,C2,C3",
        "A1,B2,C3",
        "C1,B2,A3",
    ]

このように記述した場合は、is_same を下記のプログラムのように修正します。

2 行目：split メソッド を使って、coords を Excel 座標 を要素とする list に変換 する
3 行目：excel_to_xy を使って、Excel 座標 から、x 座標 と y 座標 を計算する

1  def is_same(self, coords, mark):
2      for coord in coords.split(","):
3          x, y = excel_to_xy(coord)
4          if self.board[x][y] != mark:
5              return False
6      return True
7
8  Marubatsu.is_same = is_same

行番号のないプログラム

def is_same(self, coords, mark):
    for coord in coords.split(","):
        x, y = excel_to_xy(coord)
        if self.board[x][y] != mark:
            return False
    return True

Marubatsu.is_same = is_same

修正箇所

def is_same(self, coords, mark):
-   for coord in coords:
+   for coord in coords.split(","):
+       x, y = excel_to_xy(coord)
        if self.board[x][y] != mark:
            return False
    return True

Marubatsu.is_same = is_same

下記のプログラムを実行することで、修正した judge メソッドで、すべてのテストケースで期待された処理が行われることが確認できます。実行結果は省略します。

test_judge()

`is_winner` のアルゴリズムその 4 （データを計算で作り出す）

その 3 の方法では、プログラムの中 に直接 judge_coords_list のような、判定を行うために 利用するデータ を記述する必要があります。このような方法では、判定を行うために利用する データの数 が 増えた場合 は、データを記述 するのが大変です。そこで、次は、判定を行うために利用する データ を プログラムで作成 するアルゴリズムを紹介します。

判定を行うために利用する データ を プログラムで作成 するためには、それらの データの性質 を理解する必要があります。どのような性質があるかについて 考えてみて下さい。

判定を行うために利用するデータの性質

〇×ゲームでは、一直線上に並んだ座標は、下記の 3 種類に分類 することができます。

横方向 に並ぶ場合
縦方向 に並ぶ場合
斜め方向 に並ぶ場合

まず、横方向 に並ぶ場合の性質から考えます。どのような性質があるかについて考えてみて下さい。

横方向に並ぶ座標の性質と作成

横方向に並ぶ座標には以下のような性質があります。

どの座標も y 座標 は すべて同じ である
横方向に並ぶ座標の中の 座標の数 は、ゲーム盤の 列の数 だけ存在し、それぞれの x 座標 は 0、1、・・・、ゲーム盤の列の数 - 1 である。例えば、〇×ゲームの場合で、y 座標が 0 の場合は、(0, 0)、(1, 0)、(2, 0) となる
横方向に並ぶ座標の種類は、ゲーム盤の 行の数 だけ存在し、それぞれの y 座標 は 0、1、・・・、ゲーム盤の行の数 - 1 である。例えば〇×ゲームの場合は、「(0, 0)、(1, 0)、(2, 0)」、「(0, 1)、(1, 1)、(2, 1)」、「(0, 2)、(1, 2)、(2, 2)」の 3 種類 である

2 番目の性質 から、y 座標が 0 の場合 の横方向に並ぶ座標は、for 文 による 繰り返し処理 を使った下記のプログラムで作成することができます。

coords = []
for x in range(3):
    coords.append([x, 0])
print(coords)

実行結果

[[0, 0], [1, 0], [2, 0]]

また、上記のプログラムは、list 内包表記 を使って下記のように 簡潔に記述 できます。

coords = [[x, 0] for x in range(3)]
print(coords)

実行結果

[[0, 0], [1, 0], [2, 0]]

3 番目の性質 から、横方向に並ぶ座標 は、for 文 による 繰り返し処理 を使った下記のプログラムで作成することができます。

judge_coords_list = []
for y in range(3):
    judge_coords_list.append([[x, y] for x in range(3)])
print(judge_coords_list)

実行結果

[[[0, 0], [1, 0], [2, 0]], [[0, 1], [1, 1], [2, 1]], [[0, 2], [1, 2], [2, 2]]]

上記のプログラムは、list 内包表記を使って下記のように記述できます。ただし、下記のプログラムは わかりづらい 点と、この後 で縦方向や斜め方向に並ぶ座標を 追加する際 に list 内包表記を 使うことはできない ので、採用しないことにします。

judge_coords_list = [[[x, y] for x in range(3)] for y in range(3)]
print(judge_coords_list)

実行結果

[[[0, 0], [1, 0], [2, 0]], [[0, 1], [1, 1], [2, 1]], [[0, 2], [1, 2], [2, 2]]]

縦方向に並ぶ座標の作成

縦方向 に並ぶ座標の性質は、横方向 に並ぶ座標の性質の x 座標 と y 座標 を 入れ替えた ものです。従って、縦方向 に並ぶ座標の作成は、先程のプログラムの x と y を 入れ替える ことで、下記のプログラムのように記述できます。なお、入れ替える のは、for の直後の x と y だけで、[x, y] の x と y を 入れ替えてはいけない 点に注意して下さい。分かりづらい と思った方は、横方向 に並ぶ座標の作成の説明と 同様の手順 で、順を追って プログラムを作成してみて下さい。

judge_coords_list = []
for x in range(3):
    judge_coords_list.append([[x, y] for y in range(3)])
print(judge_coords_list)

修正箇所

-for y in range(3):
+for x in range(3):
-   judge_coords_list.append([[x, y] for x in range(3)])
+   judge_coords_list.append([[x, y] for y in range(3)])

実行結果

[[[0, 0], [0, 1], [0, 2]], [[1, 0], [1, 1], [1, 2]], [[2, 0], [2, 1], [2, 2]]]

すべて の x と y を 入れ替え ては いけない理由 は、入れ替える前 と 全く同じ処理 が行われてしまうからです。例えば、下記のプログラムの 1 ~ 3 行目と、4 ~ 6 行目は、a と b を入れ替えた プログラムですが、3 行目と 6 行目は、どちらも 同じ計算結果 が表示されます。

1  a = 1
2  b = 2
3  print(a * 3 + b)
4  b = 1
5  a = 2
6  print(b * 3 + a)

行番号のないプログラム

a = 1
b = 2
print(a * 3 + b)
b = 1
a = 2
print(b * 3 + a)

実行結果

5
5

一方、下記のプログラムのように、式のほう ではなく、データだけ を 入れ替えた 場合は、異なる計算 が行われます。

a = 1
b = 2
print(a * 3 + b)
b = 1
a = 2
print(a * 3 + b)

修正箇所

a = 1
b = 2
print(a * 3 + b)
b = 1
a = 2
-print(b * 3 + a)
+print(a * 3 + b)

実行結果

5
7

上記のプログラムは、縦方向 の座標のみを作成するので、横方向 の座標と 合わせる 場合は、下記のプログラムのように 最初の行 で、judge_coords_list に 空の list を代入し、その後で 横方向 の座標と 縦方向 の座標を作成して judge_coords_list に追加します。

judge_coords_list = []
# 横方向の座標を追加する
for y in range(3):
    judge_coords_list.append([[x, y] for x in range(3)])
# 縦方向の座標を追加する
for x in range(3):
    judge_coords_list.append([[x, y] for y in range(3)])
print(judge_coords_list)

実行結果

[[[0, 0], [1, 0], [2, 0]], [[0, 1], [1, 1], [2, 1]], [[0, 2], [1, 2], [2, 2]], [[0, 0], [0, 1], [0, 2]], [[1, 0], [1, 1], [1, 2]], [[2, 0], [2, 1], [2, 2]]]

斜め方向に並ぶ座標の作成

斜め方向 に並ぶ座標は、横や縦方向と 性質が異なり ます。その性質について考えてみて下さい。

斜め方向に並ぶ座標は、左上から右下 方向と、右上から左下 方向の 2 種類があります。

まず、左上から右下 方向の性質について考えてみます。性質が わかりづらい と思った方は 座標を実際に記述 してみることをお勧めします。〇×ゲームの左上から右下方向の場合の座標は (0, 0)、(1, 1)、(2, 2) です。一見すればすぐに下記の性質がある事がわかると思います。

どの座標 も x 座標と y 座標 は同じである
座標の数 は、ゲーム盤の 列の数 だけ存在し、それぞれの x 座標は 0、1、・・・、ゲーム盤の列の数 - 1 である

従って、左上から右下方向の座標は、下記のプログラムで作成することができます。

coords = [[x, x] for x in range(3)]
print(coords)

実行結果

[[0, 0], [1, 1], [2, 2]]

上記の性質 2 は、下記のように考えることもできます。

座標の数 は、ゲーム盤の 行の数 だけ存在し、それぞれの y 座標は 0、1、・・・、ゲーム盤の行の数 - 1 である

上記のように考えた場合は、左上から右下方向の座標は、下記のプログラムのように記述します。どちらでも計算結果は同じなので、分かりやすいと思ったほうを採用して下さい。

coords = [[y, y] for y in range(3)]
print(coords)

実行結果

[[0, 0], [1, 1], [2, 2]]

次に、右上から左下 方向の性質について考えてみます。先程と同様に〇×ゲームの場合の 座標を記述 すると (2, 0)、(1, 1)、(0, 2) のようになります。この場合の性質は少し わかりづらい かもしれませんが、ゲーム盤の サイズを増やすこと でその性質が わかりやすくなる ので記述してみます。ゲーム盤の サイズが 5 * 5 の場合は、(4, 0)、(3, 1)、(2, 2)、(1, 3)、(0, 4) となります。よく見ると、どの座標 も、x 座標と y 座標の合計 が 4 になることがわかります。この 4 が ゲーム盤の行の数 - 1 であることに 気が付く ことができれば、以下の性質があることがわかるようになります。

どの座標 も x 座標と y 座標の合計 は、ゲーム盤の行の数 - 1 である
座標の数 、ゲーム盤の 行の数 だけ存在し、それぞれの y 座標は 0、1、・・・、ゲーム盤の行の数 - 1 である。

〇×ゲームの場合、ゲーム盤の行の数 - 1 は 2 なので、x + y = 2 になるため、x 座標 は x = 2 - y という 式で計算 することができます。

従って、右上から左下方向の座標は、下記のプログラムで作成することができます。

coords = [[2 - y, y] for y in range(3)]
print(coords)

実行結果

[[2, 0], [1, 1], [0, 2]]

x 座標 を基準に考えた場合は、下記のようになります。この場合は、先程と異なり、左下から右上 方向の、(0, 2)、(1, 1)、(2, 0) の順で座標が作成されます。

coords = [[x, 2 - x] for x in range(3)]
print(coords)

実行結果

[[0, 2], [1, 1], [2, 0]]

x 座標 を基準に、先程と同じ 右上から左下 方向で座標を作成したい場合は、下記のプログラムのように、range から 取り出される値 を 2 から 0 まで 1 ずつ減らす ように記述します。この range の記述方法 については、以前の記事を参照して下さい。なお、プログラムが わかりづらい ので、わざわざ下記のように記述する 必要はない と思います。

coords = [[x, 2 - x] for x in range(2, -1, -1)]
print(coords)

実行結果

[[2, 0], [1, 1], [0, 2]]

すべての一直線に並ぶ座標の作成

すべて の 一直線に並ぶ座標 は、上記を あわせた、下記のプログラムで作成することができます。

judge_coords_list = []
# 横方向の座標を追加する
for y in range(3):
    judge_coords_list.append([[x, y] for x in range(3)])
# 縦方向の座標を追加する
for x in range(3):
    judge_coords_list.append([[x, y] for y in range(3)])
# 左上から右下方向の座標を追加する
judge_coords_list.append([[x, x] for x in range(3)])
# 右上から左下方向の座標を追加する
judge_coords_list.append([[2 - y, y] for y in range(3)])
print(judge_coords_list)

実行結果

[[[0, 0], [1, 0], [2, 0]], [[0, 1], [1, 1], [2, 1]], [[0, 2], [1, 2], [2, 2]], [[0, 0], [0, 1], [0, 2]], [[1, 0], [1, 1], [1, 2]], [[2, 0], [2, 1], [2, 2]], [[0, 0], [1, 1], [2, 2]], [[2, 0], [1, 1], [0, 2]]]

x と y の 意味がおかしくなる ことを 気にしない のであれば、縦方向 と、横方向 の座標を下記のプログラムのように、1 つ の for 文で まとめる ことができます。

まとめてもあまりプログラムが短くならず、分かりにくいので本記事では採用しません。

judge_coords_list = []
for y in range(3):
    # 横方向の座標を追加する
    judge_coords_list.append([[x, y] for x in range(3)])
    # 縦方向の座標を追加する
    judge_coords_list.append([[y, x] for y in range(3)])
# 左上から右下方向の座標を追加する
judge_coords_list.append([[x, x] for x in range(3)])
# 右上から左下方向の座標を追加する
judge_coords_list.append([[2 - y, y] for y in range(3)])
print(judge_coords_list)

実行結果

[[[0, 0], [1, 0], [2, 0]], [[0, 1], [1, 1], [2, 1]], [[0, 2], [1, 2], [2, 2]], [[0, 0], [0, 1], [0, 2]], [[1, 0], [1, 1], [1, 2]], [[2, 0], [2, 1], [2, 2]], [[0, 0], [1, 1], [2, 2]], [[2, 0], [1, 1], [0, 2]]]

`is_winner` の修正

上記のプログラムを is_winner に 組み込む ことにします。その際に、上記のプログラムの中で記述した 3 は、ゲーム盤のサイズ を表すデータで、そのデータは、Marubatsu クラスのインスタンスの BOARD_SIZE 属性 に代入されているので、3 を self.BOARD_SIZE に 置き換える ことにします。

また、右上から左下 方向の座標の追加の際に記述した 2 は、ゲーム盤のサイズ - 1 なので、self.BOARD_SIZE - 1 に 置き換えます。下記のプログラムはそのように修正したプログラムです。

def is_winner(self, player):
    # 一直線上のマスの座標を表すデータを集めた list を代入する変数を空の list で初期化する
    judge_coords_list = []
    # 横方向の座標を追加する
    for y in range(self.BOARD_SIZE):
        judge_coords_list.append([[x, y] for x in range(self.BOARD_SIZE)])
    # 縦方向の座標を追加する
    for x in range(self.BOARD_SIZE):
        judge_coords_list.append([[x, y] for y in range(self.BOARD_SIZE)])
    # 左上から右下方向の座標を追加する
    judge_coords_list.append([[x, x] for x in range(self.BOARD_SIZE)])
    # 右上から左下方向の座標を追加する
    judge_coords_list.append([[self.BOARD_SIZE - 1 - y, y] for y in range(self.BOARD_SIZE)])

    # 一直線上のマスの座標を順番に取り出す繰り返し処理
    for coords in judge_coords_list:
        # 取り出した一直線上のマスに player が配置されているかどうかを判定する
        if self.is_same(coords, player):
            # 並んでいれば player の勝利なので True を返す
            return True

    # どの一直線上にも配置されていない場合は、player は勝利していないので False を返す
    return False

Marubatsu.is_winner = is_winner

修正箇所

def is_winner(self, player):
-   # 一直線上のマスの座標を表すデータを集めた list
-   judge_coords_list = [
-       [ [0, 0], [1, 0], [2, 0] ],
-       [ [0, 1], [1, 1], [2, 1] ],
-       [ [0, 2], [1, 2], [2, 2] ],
-       [ [0, 0], [0, 1], [0, 2] ],
-       [ [1, 0], [1, 1], [1, 2] ],
-       [ [2, 0], [2, 1], [2, 2] ],
-       [ [0, 0], [1, 1], [2, 2] ],
-       [ [2, 0], [1, 1], [0, 2] ],
-   ]
+    # 一直線上のマスの座標を表すデータを集めた list を代入する変数を空の list で初期化する
+   judge_coords_list = []
+   # 横方向の座標を追加する
+   for y in range(self.BOARD_SIZE):
+       judge_coords_list.append([[x, y] for x in range(self.BOARD_SIZE)])
+   # 縦方向の座標を追加する
+   for x in range(self.BOARD_SIZE):
+       judge_coords_list.append([[x, y] for y in range(self.BOARD_SIZE)])
+   # 左上から右下方向の座標を追加する
+   judge_coords_list.append([[x, x] for x in range(self.BOARD_SIZE)])
+   # 右上から左下方向の座標を追加する
+   judge_coords_list.append([[self.BOARD_SIZE - 1 - y, y] for y in range(self.BOARD_SIZE)])    

    # 一直線上のマスの座標を順番に取り出す繰り返し処理
    for coords in judge_coords_list:
        # 取り出した一直線上のマスに player が配置されているかどうかを判定する
        if self.is_same(coords, player):
            # 並んでいれば player の勝利なので True を返す
            return True

    # どの一直線上にも配置されていない場合は、player は勝利していないので False を返す
    return False

Marubatsu.is_winner = is_winner

test_judge()

`is_winner` のアルゴリズムその 5 （差分で座標を計算する）

その 4 までの方法では、一直線上の座標 を あらかじめ 記述もしくは計算し、それを is_same メソッドの 実引数に記述 して判定を行いました。それに対し、一直線上の座標 を 計算するためのデータ を is_same メソッドの 実引数に記述 し、is_same メソッドの中で そのデータを使って座標を計算する というアルゴリズムがあります。

アルゴリズムの考え方

例えば、横方向 の座標の一つに (0, 0)、(1, 0)、(2, 0) というデータがありますが、このデータは、(0, 0) から始まり、x 座標 を 1 つずつ増やす ことで 残りのデータを計算して作成 することができます。

この性質は、他の横方向 の座標にも 当てはまります。例えば、(0, 1)、(1, 1)、(2, 1) というデータは、(0, 1) から始まり、x 座標 を 1 つずつ増やす ことで 残りのデータを計算して作成 できます。

つまり、横方向 のデータは、最初の座標 と、x 座標 を どれだけ増やす かという情報があれば、残りの座標 のデータを 計算で作り出す ことが できる ということです。

これは、縦方向 と、斜め方向 の座標にも あてはまり、必要なデータ を表にすると以下のようになります。なお、次のデータ で x 座標や y 座標 が どれだけ変化するか を表す データ の事を、差分と呼ぶので、表には x 座標の差分 のように表記しています。

データの種類	最初の座標	ｘ座標の差分	y 座標の差分
横方向のデータ	(0, 0) (0, 1) (0, 2)	1	0
縦方向のデータ	(0, 0) (1, 0) (2, 0)	0	1
左上から右下方向のデータ	(0, 0)	1	1
右上から左下方向のデータ	(2, 0)	-1	1

`is_same` の修正

まず、最初の座標 と、x、y 座標の差分 を使って判定を行うように is_same を下記のプログラムのように修正します。修正内容は以下の通りです。

1 行目：仮引数 coords を 最初の座標 を代入する coord と、x 座標と y 座標の差分 を代入する dx と dy に修正する。仮引数の名前 の d は、差分を表す 英単語 の difference の 頭文字 である。仮引数 mark は 変更しない が、先頭に移動 する（先頭に移動する理由は後述する）
2 行目：最初の座標 から、x 座標 と y 座標 を取り出して x と y に代入 する
3 行目：for 文による 繰り返しの処理 を行う。チェックする座標の数 は、ゲーム盤のサイズ と 等しい ので、繰り返しの数 を表す 反復可能オブジェクト には、range(self.BOARD_SIZE) を記述する。なお、繰り返しの数 を代入する変数は、この繰り返しの ブロックの中 で 利用しない ので、そのような値を代入 する 変数名 として、慣習的に使われる _ を使用している³
4、5 行目：(x, y) に mark が配置 されているかどうかを判定し、配置されていなければ False を返す。なお、この部分は元と同じで、修正していない
6、7 行目：x に dx、y に dy を加算することで、次の座標を計算 する。計算後の値 が、次の繰り返し の 4 行目で使用 される

 1  def is_same(self, mark, coord, dx, dy):
 2      x, y = coord   
 3      for _ in range(self.BOARD_SIZE):
 4          if self.board[x][y] != mark:
 5              return False
 6          x += dx
 7          y += dy
 8
 9      return True
10
11  Marubatsu.is_same = is_same

行番号のないプログラム

def is_same(self, mark, coord, dx, dy):
    x, y = coord   
    for _ in range(self.BOARD_SIZE):
        if self.board[x][y] != mark:
            return False
        x += dx
        y += dy

    return True

Marubatsu.is_same = is_same

修正箇所

-def is_same(self, coords, mark):
+def is_same(self, mark, coord, dx, dy):
+   x, y = coord   
-   for x, y in coords:
+   for _ in range(self.BOARD_SIZE):
        if self.board[x][y] != mark:
            return False
+       x += dx
+       y += dy

    return True

Marubatsu.is_same = is_same

座標を作成するためのデータの作成

次に、is_winner の中の judge_coords_list の データ構造 を、座標を作成 するために必要となる、最初の座標 と、x と y 座標の差分 のデータに修正する必要があります。そのようなデータを list や tuple で表現することも可能ですが、分かりやすさを重視 して、本記事では、それぞれのデータを、下記のような dict で表現 することにします。

{ "coord": [0, 0], "dx": 1, "dy": 0 }

横方向 の座標の 最初の座標 の x 座標は 0 で、x 座標の差分 は 1、y 座標の差分 は 0 なので、横方向 の座標データを 作成するために必要なデータ は、下記のプログラムで作成することができます。

なお、このデータを代入する 変数の名前 を、データの意味 に 合わせてjudge_data_list に変更しました。また、実行結果が わかりやすく なるようにするために、以前の記事で紹介した pprint で表示を行っています。

from pprint import pprint

judge_data_list = []
# 横方向の座標を作成するために必要なデータを追加する
for y in range(3):
    judge_data_list.append({ "coord": [0, y], "dx": 1, "dy": 0 })
pprint(judge_data_list)

実行結果

[{'coord': [0, 0], 'dx': 1, 'dy': 0},
 {'coord': [0, 1], 'dx': 1, 'dy': 0},
 {'coord': [0, 2], 'dx': 1, 'dy': 0}]

同様の方法 で、縦方向 と 斜め方向 の座標を作成するために必要なデータを合わせたもの、下記のプログラムで作成することができます。

# 縦方向の座標を作成するために必要なデータを追加する
for x in range(3):
    judge_data_list.append({ "coord": [x, 0], "dx": 0, "dy": 1 })
# 左上から右下方向の座標を追加する
judge_data_list.append({ "coord": [0, 0], "dx": 1, "dy": 1 })
# 右上から左下方向の座標を追加する
judge_data_list.append({ "coord": [2, 0], "dx": -1, "dy": 1 })    
pprint(judge_data_list)

実行結果

[{'coord': [0, 0], 'dx': 1, 'dy': 0},
 {'coord': [0, 1], 'dx': 1, 'dy': 0},
 {'coord': [0, 2], 'dx': 1, 'dy': 0},
 {'coord': [0, 0], 'dx': 0, 'dy': 1},
 {'coord': [1, 0], 'dx': 0, 'dy': 1},
 {'coord': [2, 0], 'dx': 0, 'dy': 1},
 {'coord': [0, 0], 'dx': 1, 'dy': 1},
 {'coord': [2, 0], 'dx': -1, 'dy': 1}]

`is_winner` の修正

is_winner は以下のプログラムのように修正します。

3 ~ 13 行目：上記の judge_data_list のデータを 作成する処理 を記述するように修正する。13 行目の 右上から左下方向 の 先頭の座標 は、ゲーム盤の 右上の座標 なので、[self.BOARD_SIZE - 1, 0] と記述することができる
16 行目：judge_data_list から順番に 取り出したデータ を judge_data に代入 するという 繰り返し処理 を行うように修正する
18 行目：is_same の 実引数 を、judge_data の属性 を使って記述するように修正する

 1  def is_winner(self, player):
 2      # 一直線上のマスの座標を作成するためのデータを集めた list を代入する変数を空の list で初期化する
 3      judge_data_list = []
 4      # 横方向の座標を作成するために必要なデータを追加する
 5      for y in range(self.BOARD_SIZE):
 6          judge_data_list.append({ "coord": [0, y], "dx": 1, "dy": 0 })
 7      # 縦方向の座標を作成するために必要なデータを追加する
 8      for x in range(self.BOARD_SIZE):
 9          judge_data_list.append({ "coord": [x, 0], "dx": 0, "dy": 1 })
10      # 左上から右下方向の座標を追加する
11      judge_data_list.append({ "coord": [0, 0], "dx": 1, "dy": 1 })
12      # 右上から左下方向の座標を追加する
13      judge_data_list.append({ "coord": [self.BOARD_SIZE - 1, 0], "dx": -1, "dy": 1 })     
14
15      # 一直線上のマスの座標作成するためのデータを順番に取り出す繰り返し処理
16      for judge_coords in judge_data_list:
17          # 取り出した一直線上のマスに player が配置されているかどうかを判定する
18          if self.is_same(player, judge_coords["coord"], judge_coords["dx"], judge_coords["dy"]):
19              # 並んでいれば player の勝利なので True を返す
20              return True
21
22      # どの一直線上にも配置されていない場合は、player は勝利していないので False を返す
23      return False
24
25  Marubatsu.is_winner = is_winner

行番号のないプログラム

def is_winner(self, player):
    # 一直線上のマスの座標を作成するためのデータを集めた list を代入する変数を空の list で初期化する
    judge_data_list = []
    # 横方向の座標を作成するために必要なデータを追加する
    for y in range(self.BOARD_SIZE):
        judge_data_list.append({ "coord": [0, y], "dx": 1, "dy": 0 })
    # 縦方向の座標を作成するために必要なデータを追加する
    for x in range(self.BOARD_SIZE):
        judge_data_list.append({ "coord": [x, 0], "dx": 0, "dy": 1 })
    # 左上から右下方向の座標を追加する
    judge_data_list.append({ "coord": [0, 0], "dx": 1, "dy": 1 })
    # 右上から左下方向の座標を追加する
    judge_data_list.append({ "coord": [self.BOARD_SIZE - 1, 0], "dx": -1, "dy": 1 })     

    # 一直線上のマスの座標作成するためのデータを順番に取り出す繰り返し処理
    for judge_data in judge_data_list:
        # 取り出した一直線上のマスに player が配置されているかどうかを判定する
        if self.is_same(player, judge_data["coord"], judge_data["dx"], judge_data["dy"]):
            # 並んでいれば player の勝利なので True を返す
            return True

    # どの一直線上にも配置されていない場合は、player は勝利していないので False を返す
    return False

Marubatsu.is_winner = is_winner

修正箇所

def is_winner(self, player):
-   # 一直線上のマスの座標を表すデータを集めた list を代入する変数を空の list で初期化する
-   judge_coords_list = []
-   # 横方向の座標を追加する
-   for y in range(self.BOARD_SIZE):
-       judge_coords_list.append([[x, y] for x in range(self.BOARD_SIZE)])
-   # 縦方向の座標を追加する
-   for x in range(self.BOARD_SIZE):
-       judge_coords_list.append([[x, y] for y in range(self.BOARD_SIZE)])
-   # 左上から右下方向の座標を追加する
-   judge_coords_list.append([[x, x] for x in range(self.BOARD_SIZE)])
-   # 右上から左下方向の座標を追加する
-   judge_coords_list.append([[self.BOARD_SIZE - 1 - y, y] for y in range(self.BOARD_SIZE)])
+   # 一直線上のマスの座標を作成するためのデータを集めた list を代入する変数を空の list で初期化する
+   judge_data_list = []
+   # 横方向の座標を作成するために必要なデータを追加する
+   for y in range(self.BOARD_SIZE):
+       judge_data_list.append({ "coord": [0, y], "dx": 1, "dy": 0 })
+   # 縦方向の座標を作成するために必要なデータを追加する
+   for x in range(self.BOARD_SIZE):
+       judge_data_list.append({ "coord": [x, 0], "dx": 0, "dy": 1 })
+   # 左上から右下方向の座標を追加する
+   judge_data_list.append({ "coord": [0, 0], "dx": 1, "dy": 1 })
+   # 右上から左下方向の座標を追加する
+   judge_data_list.append({ "coord": [self.BOARD_SIZE - 1, 0], "dx": -1, "dy": 1 })     

-   # 一直線上のマスの座標を順番に取り出す繰り返し処理
-   for coords in judge_coords_list:
+   # 一直線上のマスの座標作成するためのデータを順番に取り出す繰り返し処理
+   for judge_data in judge_data_list:
        # 取り出した一直線上のマスに player が配置されているかどうかを判定する
-       if self.is_same(coords, player):
+       if self.is_same(player, judge_coords["coord"], judge_coords["dx"], judge_coords["dy"]):
            # 並んでいれば player の勝利なので True を返す
            return True

    # どの一直線上にも配置されていない場合は、player は勝利していないので False を返す
    return False

Marubatsu.is_winner = is_winner

test_judge()

実引数に記述した dict の仮引数への展開

下記は、先程のプログラムの、18 行目のプログラムですが、このプログラムの 実引数 で、judge_data を 3 箇所に記述 するのが面倒だと思った人はいないでしょうか。

if self.is_same(mark, judge_data["coord"], judge_data["dx"], judge_data["dy"]):

Python では、dict の展開 という記法を利用することで、上記のプログラムを下記のように 簡潔に記述 することができます。

if self.is_same(mark, **judge_data):

関数呼び出し の 実引数 に、dict を記述 する際に、上記の **judge_data のように、先頭に ** を記述 することで、dict の それぞれ の「属性名 を キーワード」、「属性の値 を キーワードの値」とする キーワード引数 を記述した場合の処理が行われます。このことを、dict の展開 と呼びます。

例えば、関数の実引数として { "coord": [0, 0], "dx": 1, "dy": 0 } の前に、** を記述 して呼び出すと、coord=[0, 0]、dx=1、dy=0 という 3 つのキーワード引数 が記述されたことになります。

具体例として、下記の 3 行目と 4 行目は 同じ処理 を行うプログラムです。

mb = Marubatsu()
judge_data = { "coord": [0, 0], "dx": 1, "dy": 0 }
print(mb.is_same(Marubatsu.CIRCLE, **judge_data))
print(mb.is_same(Marubatsu.CIRCLE, coord=[0, 0], dx=1, dy=0))

実行結果

False
False

なお、dict の展開 が行われると、キーワード引数 として 実引数が記述 されるので、以前の記事で説明したように、dict の展開 は、必ず位置引数より前に記述 する必要があります。例えば、下記のように 位置引数 の Marubatsu.CIRCLE より後 に、dict の展開を記述 すると エラーが発生 します。

is_same の仮引数 mark を 先頭に記述 するようにしたのは、そのため です。

print(mb.is_same(**judge_data, Marubatsu.CIRCLE))

実行結果

  Cell In[44], line 1
    print(mb.is_same(**judge_data, Marubatsu.CIRCLE))
                                                   ^
SyntaxError: positional argument follows keyword argument unpacking

上記のエラーメッセージは、以下のような意味を持ちます。

SyntaxError
構文（文法のこと）（syntax）に関するエラー
positional argument follows keyword argument
位置引数（positional argument）が、キーワード引数（keyword argument）の後（follows）に記述されている

dict の展開を利用するためには、以下の点に注意する必要があります。

dict の キーの名前 と、関数の 仮引数の名前 を 一致させる 必要がある
すべて の キーワード引数 を dict のキーの名前 より 前に記述 する必要がある

先程の is_winner のプログラムの、18 行目のプログラムを修正し、下記のプログラムを実行することで、修正した judge メソッドで、すべてのテストケースで期待された処理が行われることが確認できます。実行結果は先程と同じなので省略します。

test_judge()

その 5 の方法の利点と欠点

その 5 の方法の利点は、ゲーム盤の サイズ が 極端に大きくなった場合 でも 利用できる 点にあります。例えば、ゲーム盤の サイズ が 1 億 * 1 億⁴ の〇×ゲームの場合、一直線上に並ぶ座標 は、縦と横 方向で 1 億通りずつ、斜め方向で 2 通り の、計 2 億 2 通り あります。それぞれ に対して、1 億 の 座標データ が記録されるので、全部で約 2 億 * 1 億 = 約 2 京 もの 座標データ が必要となりますが、現在の 一般的なコンピュータ でも、それだけのデータを 記憶することは困難 でしょう。

一方、この方法であれば、一直線上に並ぶ データ 1 つ につき、座標データが 1 つ と 差分データが 2 つ ですむので、その 4 の方法で作成するデータと比較して、約 1 億分の 1 のデータ量で済みます。

なお、その 4 の方法の欠点は、ゲーム盤のサイズが 100 や 1000 程度 では 全く問題にならない ので、〇×ゲーム、将棋、囲碁程度のサイズのゲーム盤であれば 気にする必要は全くない でしょう。

この方法の欠点としては、アルゴリズムが、その 4 の方法と比べて 抽象的 になるので、分かりづらくなる 点が挙げられます。他にも、その 4 の方法の場合は、一度作成した座標データ を 何度も再利用する（本記事では再利用はしていません）ことが可能ですが、その 5 の方法の場合は、毎回すべての 座標データ を 計算する必要 があるので、計算速度 が 若干遅くなる⁵ という欠点があります。

なお、judge メソッドの処理は、最近の PC であれば、1 ミリ秒（1/1000 秒）以下で実行できるので、〇×ゲーム を 人間が遊ぶ 場合は その差 を 気にする必要 は全く ありません。一方、〇×ゲームの AI を作成 する際には、judge メソッドなどの 処理速度 が重要になる場合があるので、アルゴリズムの計算速度 については、その際に説明する予定です。

本記事のまとめ

本記事では、judge メソッドの中の、〇と × の勝利を判定する 様々なアルゴリズムを紹介 しました。下記の表は、それぞれのアルゴリズムの 特長を簡単にまとめた ものです。

アルゴリズム	利点	欠点
修正前	初心者でも記述できる	記述が長い入力ミスをしやすい
その 1 （`+`演算子）	Python 以外の多くの言語でも記述できる	記述が長い入力ミスをしやすい
その 2 (データの分離）	データを記述しやすいプログラムを短く記述できる	データの量が多いと記述が大変
その 3 （繰り返しの利用）	その 2 の利点に加え、データを用意すれば、3 * 3 以外のゲーム盤にも対応できる	データの量が多いと記述が大変
その 4 （データの作成）	常に 3 * 3 のゲーム盤以外にも対応できるデータを記述する必要がない	プログラムが複雑
その 5 （データを差分で作成）	その 4 の利点に加えて、非常に大きなゲーム盤でも利用できる	プログラムが複雑計算速度がその 4 より若干遅い

アルゴリズム は、データ構造 と 密接な関係 があるので、〇×ゲームの ゲーム盤 のデータを、別のデータ構造 で表現した場合は、上記とは 異なるアルゴリズム を使う必要があります。別のデータ構造で〇×ゲームのゲーム盤を表現する方法と、その場合のアルゴリズムについては、〇×ゲームの AI を作成する際に紹介する予定です。

次回の記事では、他の〇と×の勝利を判定するアルゴリズムと、ゲーム盤のマスが埋まっていることを判定する他のアルゴリズムについて紹介します。

本記事で入力したプログラム

以下のリンクから、本記事で入力して実行した JupyterLab のファイルを見ることができます。

以下のリンクは、今回の記事で更新した marubatsu.py です。プログラムは、その 5 のものを記述しています。

以下のリンクは、今回の記事で更新したした test.py です。

次回の記事

更新履歴

更新日時	更新内容
2023/12/11	`is_winner` の仮引数の名前を `winner` から `player` に修正しました
2024/01/28	`is_winner` の 13 行目の `[2, 0]` を `[self.BOARD_SIZE - 1, 0]` に修正しました

記述そのものは可能ですが、Python の場合とは 全く異なる計算 が行われます ↩
C 言語など、+ 演算子 を使って文字列の 結合を行う ことが できない 言語が存在します ↩
別の名前に変更してもかまいませんが、_ は良く使われるのでその意味は覚えておいて下さい ↩
1 億という極端な例が非現実的だと思う人がいるかもしれませんが、実際にそのような大量のデータを扱うプログラムは存在し、そのような場合はその 5 のアルゴリズムを使うことはできません ↩
具体的な方法については割愛しますが、筆者の PC で比較した所、その 4 よりその 5 の judge メソッドのほうが、若干ですが、処理に時間がかかりました ↩

Pythonで〇×ゲームのAIを一から作成する その34 さまざまな勝利判定のアルゴリズム

目次と前回の記事

実装の進捗状況と前回までのおさらい

〇×ゲームの仕様と進捗状況

これまでに作成したモジュール

前回までのおさらい

judge メソッドの改良

勝利判定を行うメソッドの定義

is_winner の実装

修正した judge メソッドのテスト

is_winner の微修正

is_winner のアルゴリズム その 1 （+ 演算子を使う）

is_winner のアルゴリズム その 2 （データの分離と繰り返し処理）

条件式からのデータの分離

for 文を使った is_winner の記述

is_winner のアルゴリズム その 3 （繰り返しを使った一直線上の並びの判定）

アルゴリズムの説明

is_same の実装

is_same を使った is_winner の記述

is_winner のアルゴリズム その 4 （データを計算で作り出す）

判定を行うために利用するデータの性質

横方向に並ぶ座標の性質と作成

縦方向に並ぶ座標の作成

斜め方向に並ぶ座標の作成

すべての一直線に並ぶ座標の作成

is_winner の修正

is_winner のアルゴリズム その 5 （差分で座標を計算する）

アルゴリズムの考え方

is_same の修正

座標を作成するためのデータの作成

is_winner の修正

実引数に記述した dict の仮引数への展開

その 5 の方法の利点と欠点

本記事のまとめ

本記事で入力したプログラム

次回の記事

更新履歴

Pythonで〇×ゲームのAIを一から作成する　その34　さまざまな勝利判定のアルゴリズム

`judge` メソッドの改良

`is_winner` の実装

修正した `judge` メソッドのテスト

`is_winner` の微修正

`is_winner` のアルゴリズムその 1 （`+` 演算子を使う）

`is_winner` のアルゴリズムその 2 （データの分離と繰り返し処理）

for 文を使った `is_winner` の記述

`is_winner` のアルゴリズムその 3 （繰り返しを使った一直線上の並びの判定）

`is_same` の実装

`is_same` を使った `is_winner` の記述

`is_winner` のアルゴリズムその 4 （データを計算で作り出す）

`is_winner` の修正

`is_winner` のアルゴリズムその 5 （差分で座標を計算する）

`is_same` の修正

`is_winner` の修正