Pythonで〇×ゲームのAIを一から作成する その24 勝敗判定のテストの手法

目次と前回の記事

実装の進捗状況と前回までのおさらい

〇×ゲームの仕様と進捗状況

1. 正方形で区切られた 3 x 3 の 2 次元のゲーム盤上でゲームを行う
2. ゲーム開始時には、ゲーム盤のすべてのマスは空になっている
3. 2 人のプレイヤーが遊ぶゲームであり、一人は 〇 を、もう一人は × のマークを受け持つ
4. 2 人のプレイヤーは、交互に空いている好きなマスに自分のマークを 1 つ置く
5. 先手は 〇 のプレイヤーである
6. プレイヤーがマークを置いた結果、縦、横、斜めのいずれかの一直線の 3 マスに同じマークが並んだ場合、そのマークのプレイヤーの勝利とし、ゲームが終了する
7. すべてのマスが埋まった時にゲームの決着がついていない場合は引き分けとする

仕様の進捗状況は、以下のように表記します。

• 実装が完了した部分を 背景が灰色の長方形 で記述する
• 実装の一部が完了した部分を、太字 で記述する

これまでに作成したモジュール

以下のリンクから、これまでに作成したモジュールを見ることができます。

前回までのおさらい

前回の記事で、仕様 6、7 のゲームの勝敗判定を行う judge メソッドを実装しました。前回の記事の最後 で説明したように、judge メソッドにはいくつかバグがあります。今回の記事ではそれらのバグの見つけるためのテストの手法について説明します。

テストとは何か？

これまでの記事でも、関数やメソッドを実装したり、修正したりするたびに、その関数が 正しく実装できているかどうかを確認 してきました。このような、実装したプログラムが正しく動作するかどうかを確認する作業のことを、テスト（日本語では 検査） と呼びます。

テストを行う理由とテストの規模

プログラムに限った話ではありませんが、人間は ミスをする生物 なので、どんな作業を行う場合でも、ミスが起きる可能性 は ゼロにはなりません。そのため、何らかの作業を行う際には、一般的にその 作業の重要性 に応じた テスト（確認）の作業 を行います。

例えば、家を長い間留守にする場合は、出かける際に留守の間に泥棒に入られないように、戸締りの 確認を行います が、その際に行う 確認の作業 は、家の財産に応じ たものになるはずです。家の中に 盗まれるようなもの が あまりない 場合は 簡単な確認作業 で済ます人が多いと思いますが、大事な財産 が家にある場合は 念入りな確認作業 を行う人が多いでしょう。

テストの規模と精度

テストを行ったとしても、テストの目的が 必ず達成されるとは限りません。例えば、どれだけ念入りに時間をかけて戸締りを確認したとしても、留守の間に 絶対に家に泥棒が入らない という 保証は得られません。

また、テストは人間が行うものなので、テストそのもの にも、ミスが起きる ことがあります。例えば、確認したつもりが、うっかり 窓の鍵を 確認し忘れる ような場合です。

テストに時間と労力をかければ かけるほど テストの 精度は高く なりますが、テストに費やした時間や労力と、テストの精度は 比例しません。一般的 には、下記のグラフのように、最初 は急激に テストの精度が上昇 しますが、ある程度以上の時間や労力からは、精度が あまり 上昇しなくなります。

理想的には、テストに無限の時間と労力をかければ、テストの精度を 100% に 近づけていく ことは可能ですが、現実的 には、時間や労力は 無限に費やせるわけはありません。そこで、何らかのテストを行う際には、求めるテストの精度 と、テストに費やすことが出来る 時間と労力 の バランスを考えてテストを行う ことになります。

テストを行う範囲

一般的に、テストを行う 範囲が広いほど 、テストにかかる 時間と労力が増大 し、テストの 精度が低くなる 傾向があります。例えば、大邸宅の戸締りをすべて確認するテストと、小さな部屋の戸締りだけを確認する場合の事を考えてみて下さい。小さな部屋 であれば、確認 しなければならないことが 少ない ので、一般的に 少ない労力 で、高い精度 の戸締りを行うことが出来るはずです。

そこで、テストを行う 範囲を小さく分けて、その 範囲ごと に 複数の小さなテスト を行い、その結果を うまくまとめる ことで、全体のテストを行う ということが良く行われます。また、大きな範囲を一度でテストするよりも、そのような方法のほうが 効率よく テストを 行うことが出来る 場合が多いことが わかっています。

例えば、学力テスト では、一度のテストですべての学力を測るのではなく、国語、数学、英語のように、細かい分野に分けて テストを行います。また、そうやって測定した個々のテストの結果を 総合的に判断 したものを、その人の 学力 と みなします。

このような、「そのままでは解決できない大きな問題を小さな問題に分割し、そのすべてを解決することで、最終的に最初の問題全体を解決する」という手法の事を、分割統治法 と呼びます。

プログラムの場合でも同様で、これまでに行ってきたように、プログラム全体を一度にテストするのではなく、最初は関数などの 小さな単位ごと にテストを行うのが 一般的 です。関数やメソッドなどの 小さな単位 に対して行うテストの事を、単体テスト と呼びます。単体テストは、関数やメソッドを 実装 したり、その内容を 修正した際 に行います。

本記事では、以後は単体テストのことを、単に テスト と表記します。また、関数やメソッドに対するテスト という表記は長いので、以降は単に 関数のテスト と表記します。

プログラムのテストには、他にも結合テストや統合テストなど、様々な種類 があります。結合テストや統合テストは、単体テストでは発見できないようなバグを発見するためのテストで、複数のモジュールを 組み合わせた ような 大規模なプログラムを実装する際 に行われます。

結合テストや統合テストなどは、単体テストに比べて時間と労力が必要となるようなテストです。本記事で取り扱うような個人が作成する 小規模なプログラム では、それらのテストに費やす 時間と労力 が、得られるメリットに 釣り合わない 場合などではあまり行われません。本記事でもそれらのテストは行いません。

他にも様々なテストの手法がありますが、その種類は多岐にわたり、すべてを説明しようとすると一冊の本になるくらいの分量になってしまいます。本記事では数あるテストの中で、小規模なプログラム で良く使われる 手法の一つ を紹介します。他のテストの手法に関して興味がある方は調べてみると良いでしょう。

プログラムのテストを行う目的

プログラムで何らかの処理を実装した際に、バグが発生する可能性 は 常に存在 します。プログラミングの技術がどんなに上達したとしても、その可能性を ゼロにすることはできません。例えば、1 という数字を間違って 2 と入力しただけで、バグは発生します。

ある程度以上の規模の プログラムを実装 した際に、一度で バグが存在しない プログラムを 実装する のは 現実的には不可能 だと考えたほうが良いでしょう。従って、プログラムには バグがつきもの で、ほぼ確実に バグを修正する作業 が 必要 になります。

プログラミングは、バグとの闘い だと言っても過言ではありません。そのため、バグを 早期に発見する ような 工夫 や、バグが発生した際に バグの原因を発見しやすくする ような 工夫 を行うことが 非常に重要 です。テスト はそのような 工夫の一つ です。

プログラムのテストは、大きく分けて以下の 2 つの目的で行います。

• 実装したプログラムが、仕様通りに 正しく動作するかどうかを確認 する。バグを 早期に発見し、発見できれば その場で修正する ことが出来るようにする
• テストを行った部分に バグが存在 する 可能性を低くする。将来バグが発生 した際に、バグが存在する 可能性が高い場所 を絞り込んで、効率よく見つける ことが出来るようにする

関数のテスト は、胃カメラなどの、臓器の検診 に似ている所があります。定期的に 臓器の検診を行っておく ことで、臓器に病気がないかどうかを 早期に発見 することが出来ます。これは、関数の 修正、実装 を行った際に テストを行う ことに相当します。

また、病気になった場合 に、病気の原因を、検診で 正常だとみなされた 臓器を 除いて調べる ことで、効率よく 見つけることが出来ます。これは、テストを 行っていない部分 に 絞り込んで バグを 効率良く 見つけることに相当します。

前者の目的の意味と重要性は直観的に理解できると思います。後者の目的も 非常に重要 ですが、初心者にはわかりにくいかもしれませんので詳しく説明します。

他にも「ソフトウェアの開発コストの削減」、「ソフトウェアのパフォーマンスの向上」などのメリットがあります。下記に関連するページを紹介します。

テストによるバグの絞り込み

プログラムのテストは、バグを 100% 無くすために行うものだと 思っている人がいるかもしれません が、先程説明したように、どんなに時間をかけた テストでも、バグを 100% 発見できるとは限りません。テストによって、バグを完全に無くすことができるという考えを持っている人は その考えを捨てたほうが良いと思います。

テストがバグを 100 % 発見できないのであれば、テストを行う意味がないのではと思う人がいるかもしれませんが、先程のグラフのように、簡単なテスト であっても、ある程度の精度を得る ことができます。そのため、簡単なテストであっても、事前にテストを行っておく ことで、後からバグが発生した場合に、バグが存在する可能性が高い場所 を 絞り込む ことで 効率よく探す ことが出来るようになります。

テストを行ったということは、行ったテストで発見できるようなバグ が起きる 可能性が低い ということを意味します。そのため、バグが発生した際に、それまでに行ったテストで 発見できるようなバグの可能性を排除 して 絞り込んで探す ことが出来ます。

現実世界で 問題が起きた時の対処法 のことを考えてみて下さい。発生した問題に対する 原因の可能性が複数ある 場合は、原因の 可能性が高いものから チェックを行うのが一般的ではないでしょうか？例えば、テレビのリモコンが動作しなくなった場合に、真っ先に調べるのは 電池の残量 ではないでしょうか？リモコンを高い所から落下させたような、強い衝撃を与えた場合でもない限り、リモコンの中の特定の回路が故障したと真っ先に思い浮かべる人は ほとんどいない でしょう。

上記のリモコンの例では、問題が発生してから原因を調べましたが、事前に 電池の残量をチェックしてあれば、電池をチェックするという 手間を省いて、次に 故障の 可能性の高い原因 をチェックすることができます。プログラムのテストも同様で、あらかじめ 発生する 可能性が高そうな バグがないかどうかを 事前にテストしておくこと で、バグが発生した場所を 効率よく探す ことが 出来るようになります。

このように、プログラム で行うテストと、現実の世界 で行うテスト（検査）は、その 性質や目的 は多くの点で 良く似ています。

なお、テストはすべての関数に対して必ず行う必要がある わけではありません。テストをするまでもないような 単純な処理 しか行わないような関数であれば、テストを省略する ことは良くあります。一般的に、テストにどの程度の労力をかけるかは、関数で行われる 処理の複雑さ によって変わります。特に、実装した関数が正しく動作するかどうかが 自信が持てないような場合 は、ある程度の 労力をかけるべき でしょう。複雑な関数のテストを省略した結果、後からバグが見つかった場合 は、そのバグを修正するために 非常に大きな手間がかかる 事が良くあります。急がば回れ という格言があるように、簡単なテストでも構わない ので 複雑な関数 に対してはテストを 行ったほうが良い でしょう。

テストに関するまとめは以下のようになります

• テストを行うことで、ある程度の精度 で バグを発見する ことができる
• 時間と労力をかけるほど テストの 精度は上がる が、100 % にはならない
• テストによってすべてのバグを発見することができると 考えるべきではない
• テストを行うことで、後からバグが発生 した場合に、バグが発生した 可能性の高い場所 を 絞り込んで、効率よく探す ことが出来るようになる
• テストにかける 時間と労力 は、求める テストの 精度 と 費やすことが出来る時間と労力 を 考慮した上で決める

プログラミングが上達すればするほど、プログラムのミスが少なくなるので、テストを行う必要が少なくなくなると思っている人がいるかもしれませんが、それは 大きな間違い です。プログラミングが上達すればするほど、テストの 重要性が身に染みてわかる ようになるからです。

熟練者は どのような場合 にバグが 発生しやすいか がわかるようになるので、テストが 必要な場合 に 効率よく テストを行うことができるようになります。そのような意味では、テストに費やす時間が減るというのは正しいかもしれません。

例えば、運転免許を取り立ての人は、経験が足りない ので運転中にどのような危険があるのかが よくわかりません。そのため、ありとあらゆる場合で注意を向ける 人もいれば、人が飛び出してくる可能性が高い 危険な場面での注意を怠る 人もいるでしょう。一方、ベテランの運転手は、危険が潜んでいる可能性の高い場所が 経験からわかっている ため、効率よく注意を向けながら 運転を行うことが 出来るようになります。また、その際に、危険が潜んでる可能性が高い 場所に対して 注意を怠る ようなことは しなくなるでしょう。

関数のテストの実施方法

前回の記事で実装した、勝敗判定を行う judge メソッド より前 に実装した関数やメソッドは、行う処理が 単純なもの ばかりだったので、単純なテスト で済ましていました。一方、 judge メソッドはこれまでに実装してきた関数と比べて 複雑な処理を行っている ので、そのテストで行う作業も少々 複雑になります。

関数のテストは、様々なデータ に対して関数を何度も呼び出し、それぞれのデータ で 正しい処理 が 行われるかどうかを確認 します。ここでいうデータとは、関数の場合は関数に渡す 実引数、メソッドの場合は インスタンスの属性 や 実引数 などが挙げられます。

先程のノートで説明したように、テストには 様々な手法 があります。今回の記事で説明するテストの手法は、その中の一つにすぎません。

テストケース

テストのために 作られたデータ の事を テストデータ と呼び、それぞれのテストデータに対して関数呼び出しを行った際に、期待される処理 が行われているかどうかを確認します。テストデータと、期待される処理を組み合わせたものを、テストケース と呼びます。

企業が作成するソフトなどで行われる、本格的なテスト で用意するテストケースは、上記よりは 複雑 なものになりますが、個人で行うような 小規模なソフトのテスト では、上記のような シンプルなテストケース で 十分 でしょう。参考までに、Wikipedia のテストケースの項目のリンクを下記に示します。

期待される処理は 関数によって異なります が、多くのテストでは、関数が 特定の返り値を返すこと が期待する処理になります。今回の記事ではそのようなテストを紹介します。

他の期待される処理としては、特定の文字列が表示される があり、実際に これまでに行ってきた display_board メソッドの 確認作業 などでは、実行結果を見る ことで、そのことを確認 してきました。

他にも、place_mark のような 返り値を返さないメソッド の場合では、インスタンスの 属性の値 が 特定の値に変化する などがあります。

例えば、2 つの 実引数の合計 を計算した値を 返り値として返す 関数であれば、以下の表のようなテストケース（テストデータと、期待される処理）が考えられます。下記の表は 一例 で、下記の表 以外 のテストケースを 用意しても構いません。

テストデータ（実引数）	期待される処理（返り値）
1 と 2	3
2 と 3	5

judge メソッド の場合は、下記の表のようなテストケースが考えられます。他にも、期待される処理が 引き分け を表す Marubatsu.DRAW のテストケースが考えられるでしょう。

テストデータ	期待される処理（返り値）
〇が勝利している Marubatsu クラスのインスタンス	Marubatsu.CIRCLE
×が勝利している Marubatsu クラスのインスタンス	Marubatsu.CROSS

全数テストと抜き取りテスト

上記の表のように、一部の状況 に対するテストケースを用意して行うテストの事を、抜き取りテスト と呼びます。一方、すべての状況 に対するテストケースを用意してテストを行うことを、全数テスト と呼びます。

理想的 には、全数テストを行うことで、最も精度の高いテスト を行うことが出来ますが、現実的 には全数テストを行うことが 不可能 または、非常に困難 な場合が良くあり、そのような場合は、抜き取りテストを行います。

例えば、先程の 2 つの実引数の合計 を計算する関数の場合は、2 つの実引数の 組み合わせは無限 にあるので全数テストを行う事は 不可能 です。judge メソッドの全数テストを行う場合は、〇×ゲームの すべての局面の数 だけテストケースを用意する必要があり、その数は 膨大な数になる¹ ので全数テストを行うのは不可能ではありませんが 簡単ではありません。そのため、本記事でも judge メソッドでは 抜き取りテスト を行います。

抜き取りテストでは、一般的に、テストケースが 多いほど テストの 精度が上がります が、その反面テストの 手間が大きくなる という欠点があります。また、やみくもにテストケースを増やせば良いというわけではなく、品質の良いテストケース を用意することが 重要です。品質の良いテストケースを用意する方法についてはこの後で説明します。

テストの手順

関数のテストは、用意したすべてのテストケースに対して順番に、以下の手順で行います。

1. テストデータに対して 関数呼び出しを行う
2. 関数呼び出しの結果、期待される処理 が行われたかどうかを 確認する
3. 期待される処理が 行われていた場合 は手順 5 へ
4. 期待される処理が 行われていない場合 は、エラーメッセージを表示 する
5. 次のテストケース に対して 手順 1 からの処理を行う

要約すると、「すべてのテストデータに対して 順番に関数呼び出しを実行 し、期待される処理が 行われていない場合 に エラーメッセージを表示 する」という処理を行います。

上記のテストで確認できるのは、関数がテストデータに対して、期待される処理が行われる ということです。関数が 正しい処理 を行うことを 確認 できる わけではない 点に注意して下さい。例えば、下記の add という関数は、3 行目の返り値を計算する式で、+ の代わりに * を記述しているため バグがあります が、テストデータとして、2 つの 0 を実引数としてこの関数を呼び出すと、偶然 0 + 0 と 0 * 0 の答えが等しいので、期待される処理 である 0 が 返されてしまいます。そのため、このテストケースでテストを行っても バグを発見できません。

def add(x, y):
    # この式は間違っている。正しくは return x + y
    return x * y 

print(add(0, 0))

テストケースを 増やす ことで、バグを発見できる 確率は高くなります が、実際に、テストケースを増やしてもバグを 発見できない場合があります。先程のノートで、「テストによってすべてのバグを発見することができると 考えるべきではない」と説明したのは、そのような場合があるからです。

上記の手順を見て、期待される処理が 行われた場合 にも メッセージを表示する必要がある のではないかと 思う人がいる かもしれませんので補足します。

数多くの テストケースに対して 期待される処理が行われた場合 に メッセージを表示する と、画面がメッセージで 埋め尽くされてしまう ことになります。テストで 知りたいこと は、一般的 に期待される処理が 行われなかったこと なので、期待される処理が行われたことを 知る必要がない 場合は、メッセージを 表示しない場合が多い ようです。

テストに 時間がかかる ような場合は、途中経過を知らせる ために、期待される処理が 行われた数 を表示するような場合もありますが、その際には画面がメッセージで埋め尽くされないような 工夫を行う のが一般的です

制御フローテスト

関数のテストには、関数のブロックの中で行われる 処理を熟知 した上で行う ホワイトボックステスト と、関数の 利用方法だけを理解 して行う ブラックボックステスト² があり、それぞれでテストの 手法が異なります。自分で定義した関数 の場合は、その中で行われる処理を熟知しているので、本記事で行うテスト は ホワイトボックステスト です。

ホワイトボックステストにもいくつか種類がありますが、本記事ではその中で良く使われ、比較的 簡単に実施 することが出来る 制御フローテスト について説明します。

フロー とは、プログラムに記述した文を実行する 順序を表す流れ（flow）の事で、前回の記事 で説明した フローチャート で図示することが出来ます。プログラムは、通常は 最初の行から 順番に文が実行 されますが、if 文、for 文、関数呼び出し などによって、プログラムを実行する流れを 制御 します。制御フローテストでは、それらの中で、if 文などによる 条件分岐 によって 制御 される フロー に 注目したテスト を行います。

制御フローテストは、テストデータに対する関数呼び出し によって、記述したプログラムの処理の 流れ や 実行 が どれだけ網羅されるか によって、命令網羅、分岐網羅、条件網羅 などの種類があります。制御フローテストは、網羅（coverage）をテストするので、カバレッジテスト と呼ぶ場合があります。

制御フローテストは、複雑なもの ほどテストの 精度が上がる 反面、テストケースを用意する 手間が増大する という欠点があるため、どれを選ぶかについては 状況に応じて選択する 必要があります。

今回の記事では、それぞれの種類について 目的、利点、欠点 などの 性質 について説明します。それぞれを使った具体的なテストの方法については次回の記事で説明します。

命令網羅（statement coverage）

すべての文 を最低でも 1 度は実行する テストです。文（statement）として記述された、すべての 命令を網羅 して実行するので 命令網羅 と呼びます。英語表記の頭文字をとって SC や、C0 と略して呼ぶ場合があります。

命令網羅の目的

複数のテストデータを使って関数を呼び出した際に、関数のブロックの中で、一度も実行されない文 があった場合、その文はテストされていない ということになります。命令網羅テストを行うことで、テストされていない文が存在しない ことが保証されます。

命令網羅の例とフローチャート

命令網羅は、すべての文が実行されれば良いので、例えば、下記のような else が記述されない if 文の場合は、条件式が True になる テストケースのみ が必要となります。

if a > 1:
    print(a)

下図は、条件式が True になる 1 つ の テストケースによって行われた命令網羅のテストのフローチャートです。赤い線 が行われた 処理の流れ、赤い枠の図形 が実行された 処理と条件分岐 を表します。命令網羅では、すべての処理と条件分岐を実行する ので、下図のように、すべての図形が赤い枠で囲まれます。一方、下図で 灰色の線が存在 するように、すべての処理の流れが実行 されるとは 限りません。

下図には、条件式が 1 つしか存在しませんが、条件式が 複数あった場合も同様 です。

命令網羅の性質

命令網羅は 最も単純 な制御フローテストなので、用意する必要がある テストケースの数が最も少なく、最も簡単に行う ことができますが、その反面テストの 精度は最も低くなります。実際に、上記の例のフローチャートからわかるように、すべての処理の流れ をテストできるとは 限りません。

ただし、最も精度の低い命令網羅であっても、テストを 行わないよりまし です。実際にこれまでの記事で行った関数の確認作業の多くは命令網羅テストに相当するものでした。

なお、条件分岐が 一つも記述されていない 関数のテストは、命令網羅になります。

分岐網羅（decision coverage）

すべての条件分岐 の 条件式 が True と False の それぞれで 1 度は実行 されるようなテストです。条件分岐のすべての 分岐を網羅 するので 分岐網羅 と呼びます。英語表記の頭文字をとって DC や、C1 と略して呼ぶ場合があります。

分岐網羅の事を、英語表記の decision から、判定条件網羅 と呼ぶ場合がありますが、おそらく次で説明する条件網羅と 名前が似ていて紛らわしい ので、分岐網羅のような 意訳 のほうが良く使われるのでないかと思います。日本語の名前が紛らわしいと思った場合は、C0、C1 の表記を使うと良いでしょう。本記事でも、以降は命令網羅と分岐網羅の事を、命令網羅(C0)、分岐網羅(C1) のように表記します。

分岐網羅(C1) の目的

複数のテストデータを使って関数を呼び出した際に、関数のブロックの中で、一度も実行されない分岐 があった場合、その分岐はテストされていない ということになります。分岐網羅(C1) を行うことで、テストされていない分岐が存在しない ことが保証されます。

すべての分岐を辿ることで、すべての処理を実行する ことになるので、分岐網羅(C1) は命令網羅の条件を 必ず含みます。

分岐網羅(C1) の例とフローチャート

先程のような、else が記述されていない if 文であっても、条件式が True と、False になる 2 つのテストケースが必要 になります。また、if 文に elif が記述 されている場合は、その数だけ テストケースが必要になります。

下図は、条件式が True と False になる 2 つの テストケースによって行われた分岐網羅(C1) のテストのフローチャートです。赤の線 と 赤の枠の図形 が 条件式が True の場合、緑の線 と 緑の枠の図形 が 条件式が False の場合 に行われた 処理の流れ、処理、条件分岐 を表します。

分岐網羅(C1) では、すべての処理と条件分岐が実行される ので、下図のように、すべての図形 が 赤または緑で囲まれます。同様に、すべての処理の流れが実行される ので、すべての線 が 赤または緑になります。

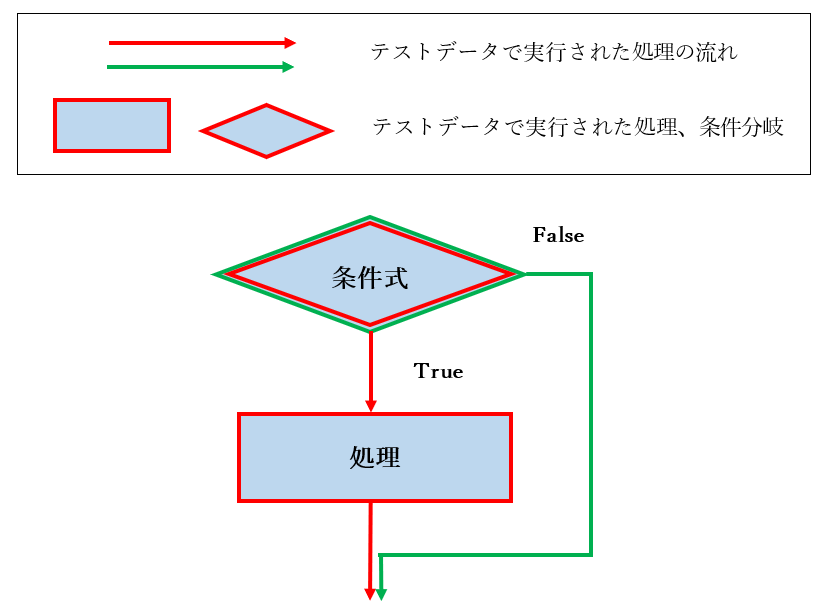
分岐網羅(C1) の性質

分岐網羅(C1) の条件 を満たす場合は、必ず命令網羅(C0) の条件も満たす ので、命令網羅(C0) よりも 少し複雑 で 精度の高い テストを行うことが出来ます。そのため、一般的には、命令網羅(C0) よりも少し 多くのテストケースが必要 となります。

条件式の中に and や or 演算子 が記述されるような、複雑な条件文 が記述されている場合は、分岐網羅(C1) だけでは バグを見つけられない可能性がある ので、この後で説明する 複数条件網羅(MCC) や 改良条件判断網羅 などを使ったほうが良いでしょう。ただし、分岐網羅(C1) は、それらと比べて用意する必要がある テストケースの数が少ない ので、そのような場合でも、時間がない場合や、条件文があまり複雑でない場合は、分岐網羅(C1) で済ますことがあります。

条件網羅（condition coverage）

条件分岐の 条件式の中 に、and または or の 論理演算子 が記述されている場合、それらで連結された それぞれの式 が True と False の それぞれで 1 度は実行 されるようなテストです。条件式の中の個々の 条件を網羅 するので 条件網羅 と呼びます。英語表記の頭文字をとって CC や、C2 と略して呼ぶ場合があります。

なお、条件式の中に and または or の論理演算子が 記述されていない 場合は、条件網羅や、この後で説明する複数条件網羅(MCC) などのテストを 行うことはできません。

本記事では、以後は条件網羅の事を、条件網羅(C2) のように表記します。

条件網羅(C2) の目的

条件式の中に、複数の式 を and または or の論理演算子で連結して 記述する ということは、それらの式の計算結果が True になる場合と False になる場合を 想定しているはず です（理由は下記のノートを参照）。条件網羅(C2) を行うことで、条件式の中のすべての式が、True と False の両方になる場合 でテストが行われることが 保証されます。

例えば、2 > 1 and a > 1 のような条件式の場合、2 > 1 の部分は 必ず True になる ので、この条件式は True and a > 1 となります。従って、この条件式の 2 > 1 のように、必ず True または False になるような式 は 記述する必要はありません。上記の場合は、a > 1 のように、その部分を 削除する ことが出来ます。

条件網羅(C2) の例

例えば、下記のプログラムでは、if 文の条件式の中に or で連結 された a > 1 と b > 2 という 2 つの式 が存在します。この場合、この 2 つの式が True と False の それぞれで 1 度は実行 されるようなテストケースが必要になります。

if a > 1 or b > 2:
    print(a, b)

条件網羅(C2) を満たすテストケースの例として、下記の表のような、a > 1 と b > 2 が「共に True」、「共に False」 になるような 2 つ のテストケースが挙げられます。

	a > 1	b > 2
テストケース 1	True	True
テストケース 2	False	False

他にも、下記の表のようなテストケースを用意することで条件網羅(C2) を満たすテストを行うことが出来ます。a > 1 と b > 2 の列を それぞれ縦に見た時 に、全体として、True と False の 両方が含まれる ようなテストケース であれば良い ということです。

	a > 1	b > 2	a > 1 or b > 2
テストケース 1	True	False	True
テストケース 2	False	True	True

条件網羅(C2) の性質

条件網羅(C2) の条件を満たしたからと言って、必ずしも分岐網羅(C1) や命令網羅(C0) の条件を 満たすとは限りません。例えば、上記の 2 つ目の表 のようなテストケースを用意した場合、表の右の列からわかるように、a > 1 or b > 2 は どちらのテストケースでも True になるので、この 2 つのテストケースで 条件網羅(C2) のテストを 行うことはできません。

条件網羅(C2) は 個人的 には 中途半端な精度のテスト なので あまり行われない と思います。本記事でも、条件網羅(C2) のテストは行いません。

複数の条件分岐が記述されている場合

具体例は示しませんが、複数 の条件分岐が記述されている場合は、それぞれの条件分岐で 個別に 条件網羅を満たすようなテストケースを用意します。ただし、それぞれの条件分岐で用意したテストケースで 内容が重複 する場合は、重複したものを削除 します。これは、この後で紹介する、他の 条件網羅の性質を持つ テストでも 同様 です。

判定条件/条件網羅 :（condition / decision coverage）

判定条件網羅（分岐網羅の別名）(C1) と条件網羅(C2) の両方を満たすようなテストです。英語表記の condition coverage と decision covarage の頭文字をとって DC/CC や、CDC と略して呼ぶ場合があります。日本語の場合は、判断条件網羅 や 条件判断網羅 のように呼ぶ場合もあるようですが、どの 日本語の呼び方 も、意味が分かりづらい ので、どちらかの 英語表記の略 を使ったほうが わかりやすいかもしれません。

本記事では以降は、判定条件/条件網羅のことを、CDC と表記します。

CDC の目的

CDC の目的は明確で、分岐網羅(C1) と、条件網羅(C2) の 両方の性質 を持つテストを行うことです。

CDC の例

if a > 1 or b > 2:
    print(a, b)

上記の、先程のと同じプログラムの場合は、条件網羅(C2) の例で 最初に紹介 した下記の表の 2 つのテストケースのように、条件式の中の それぞれの式の計算結果 と、条件式の計算結果 が、1 度は True と False になるようなテストケースが必要になります。

	a > 1	b > 2	a > 1 or b > 2
テストケース 1	True	True	True
テストケース 2	False	False	False

CDC の性質

CDC は、分岐網羅(C1) と、条件網羅(C2) の両方の性質を満たしますが、and または or 演算子で連結された 式の値 と、条件式の値 の 因果関係 を 完全にチェックできない 可能性があるという 欠点 があります。意味が分かりづらいと思いますので、具体例を挙げて説明します。

先程の、a > 1 or b > 2 は、or 演算子で連結された、a > 1 と b > 2 が 両方とも False の場合は False、片方でも True の場合は True になるという条件式です。

テストケース 2 の場合は、a > 1 と b > 2 の両方が False なので、条件式の値が False になりますが、この時、どちらの式の値 を True に変化 させても、条件式の値が True に変化 します。このことから、a > 1 が False であることと、b > 2 が False であることの、両方が原因 で、条件式の値が False になることがわかります。従って、テストケース 2 でテストを行うことで、a > 1 と b > 2 の 両方が False になっていることが 原因 で、条件式の計算結果 が False になる ことを確認することが出来ます。

一方、テストケース 1 の場合は、a > 1 と b > 2 の両方が True なので、条件式の値が True になりますが、この時、どちらか 片方の式の値 を False に変化 させても、条件式の値は True のまま 変化しません。このことから、このテストケースでテストを行っても、a > 1 が True であることと、b > 2 が True であることの、どちらが原因 で条件式の計算結果が True になるかを確認することが 出来ません。

この因果関係が特定できないということが、テストを行う際に何故問題になるかについて、おそらくピンとこない人が多いのではないかと思いますので、別の例で説明します。

工場で 10 個 の ON/OFF ができるボタン が付いた装置が作られている状況を思い浮かべて下さい。この装置は、10 個のうち、1 つ以上 のボタンを ON にすると アラーム音が鳴り、すべてを OFF にすると アラーム音が消える という装置です。この装置 が正しく動作するかどうかを テスト する際に、以下の 2 種類のテストケースで十分だと思いますか？

• すべてのスイッチを ON にした状態で アラームが鳴る ことを確認する
• すべてのスイッチを OFF にした状態で アラームが消える ことを確認する

上記のテストケースによるテストは、10 個のスイッチを すべて ON にすることで、10 個のスイッチをまとめてテスト しているようなものですが、さすがにそれでは 不十分なテスト になってしまう事は誰でも直観的に理解できるでしょう。

実は、上記のようなテストは、CDC の 性質を満たす テストを行っています。この装置を python のプログラムで表現すると、下記のような、if 文の 条件式 で、10 個の式 を or 演算子で連結 したプログラムになります。

if 式1 or 式2 or 式3 or 略 or 式10:
    アラームを鳴らす
else:
    アラームを消す

このプログラムに対して、下記の 2 種類 の テストケース でテストを行うことで、CDC でテストを行うことができます。その理由は、すべて の 式 と、条件式 の値が 1 度は True と False に なるからです。

	式1	式2	略	式10	条件式
テストケース 1	True	True	True	True	True
テストケース 2	False	False	False	False	False

この 2 種類のテストケースは、先程の「すべてのスイッチが ON にした状態でアラームが鳴ることを確認する」、「すべてのスイッチを OFF にした状態でアラームが消えることを確認する」に 相当します。このことから、CDC でテストを行うことが 不十分な場合がある ことが実感できたのではないでしょうか？

複数条件網羅（multiple condition coverage）

条件分岐の 条件式の中 に、and または or の 論理演算子 が記述されている場合、それらで連結された それぞれの式 が True と False の すべての組み合わせ で 1 度は実行 されるようなテストです。英語表記の頭文字をとって MCC と略して呼ぶ場合があります。

本記事では以降は、複数条件網羅のことを、複数条件網羅(MCC) と表記します。

複数条件網羅(MCC) のことを C2 と呼ぶ 場合もある ようです。フロー制御テストの用語は、統一されていないものがある ようなので、それらの用語を使用する場合は、用語がどのような意味で使われているかを 確認したほうが良い でしょう。

複数条件網羅(MCC) の目的

複数条件網羅(MCC) によるテストでは、それぞれの式が True と False の すべての組み合わせで 1 度は実行されるので、条件式の計算結果が 1 度は True と False になります。従って、複数条件網羅(MCC) は、分岐網羅(C1) と 条件網羅(C2) の 両方の性質 を持ちます。また、すべての組み合わせで 漏れなく確認する ので、それぞれの式の値と、条件式の値の因果関係を 気にする必要はありません。

条件式の計算結果が 1 度は True と False になる 理由は、and、or 演算子はいずれも、何らかの組み合わせ で 必ず True と False の 両方の値を取る からです。

複数条件網羅(MCC) の例

条件式が a > 1 or b > 2 の場合は、下記の表の 4 通り のテストケースを用意する必要があります。

	a > 1	b > 2
テストケース 1	True	True
テストケース 2	True	False
テストケース 3	False	True
テストケース 4	False	False

複数条件網羅(MCC) の性質

複数条件網羅(MCC) は、制御フローテストの中で、最後に説明する、経路組み合わせ網羅の次に 精度の高い テストを行うことが出来ますが、and や or で連結された式が n 個 の場合は、$2^n$ 個 のテストケースが必要になるという欠点があります。例えば、$n = 10$ の場合は、1024 個ものテストケースが必要になります。このような、組み合わせの数が膨大になる ことを、組み合わせ爆発 と呼びます。

複数条件網羅(MCC) は 組み合わせ爆発が起きやすい ので、現実的 にテストケースを用意することが 不可能な場合 が良くあります。

改良条件判断網羅（modified condition / dicision coverage）

条件分岐の 条件式の中 に、and または or の 論理演算子 が記述されている場合、それらで連結された それぞれの式の値 が、全体の条件式 の計算結果に 影響を及ぼす（因果関係がある）かどうかを 考慮 したテストを行います。英語表記の頭文字をとって MC/DC と略して呼ぶ場合があります。他にも、改良条件判定と呼ばれる場合もあるようです。

表記が長いので、本記事では以降は改良条件判断網羅のことを、MC/DC と表記します。

MC/DC の目的

MC/DC の目的は、分岐網羅(C1) と 条件網羅(C2) の 両方の性質を満たす テストを、最小限のテストケース で行うことです。

MC/DC のテストケースの求め方

a > 1 or b > 2 or c > 3 を例に説明します。この条件式の中の、それぞれの 式の計算結果 の すべての組み合わせ は下記の表のように 8 通りの組み合わせになります。それぞれを 区別できるように、表の左の列に 番号 を付けてあります。

番号	a > 1	b > 2	c > 3	条件式の値
1	True	True	True	True
2	True	True	False	True
3	True	False	True	True
4	True	False	False	True
5	False	True	True	True
6	False	True	False	True
7	False	False	True	True
8	False	False	False	False

表からわかるように、この条件式は、a > 1 が True の場合は、残りの b > 2 と c > 3 の 計算結果に関わらず、True になります。従って、a > 1 が True の場合は、残りの式の計算結果は、条件式の値 に 影響を与えない ので、a > 1 が True であること が、条件式の値が True であることの 原因 と 考える ことが出来ます。

このことから、a > 1 が True である、1 ~ 4 番の 4 つのテストケース は下記の表のように、一つにまとめる ことが出来ます。表の Any は、True か False の どちらでも良い、すなわち条件式の値に 影響を与えない ということを表します。Python に Any という特殊なデータが 存在するわけではない 点に注意して下さい。

番号	a > 1	b > 2	c > 3	条件式の値
1 ~ 4	True	Any	Any	True
5	False	True	True	True
6	False	True	False	True
7	False	False	True	True
8	False	False	False	False

前回の記事 で説明したように、Python では and と or 演算子による演算を行う際に、短絡評価 が行われることがあるので、a > 1 が True の場合 は、実際に b > 2 と c > 3 は、いずれも 計算が省略 されます。従って、上記の表のように、1 ~ 4 のテストケースを 1 つにまとめることは、理にかなっています。

a > 1 が False の場合は、それだけでは 条件式の値は決まらない ので、残りの式の計算結果を調べる必要があります。そこで、次に b > 2 が True の場合を考えることにします。先程と 同様の理由 で、この場合は c > 3 の 計算結果に関わらず、条件式の値が True になります。従って、先程と同様に、5 と 6 のテストケースは、下記の表のように、一つにまとめる ことが出来ます。

番号	a > 1	b > 2	c > 3	条件式の値
1 ~ 4	True	Any	Any	True
5、6	False	True	Any	True
7	False	False	True	True
8	False	False	False	False

a > 1 と b > 2 が 共に False の場合は、c > 3 の 計算結果 によって、条件式の値が変化する ので、7 と 8 を まとめることはできません。

上記の事から、a > 1 or b > 2 or c > 3 を、MC/DC でテストする際に必要なテストケースは、上記の表の 4 つであることがわかります。表の、1 ~ 4 に対応するテストケースは、1 ~ 4 のうちの どれか 1 つを選択する ことになります。5、6 も同様です。

上記の例では、先頭の a > 1 から順番 に調べていきましたが、b > 2 や c > 3 から調べても 論理的には MC/DC のテストを行うためのテストケースを求めることができます。ただし、Python の and と or 演算子では、短絡評価が行われるので、先頭の式から順番に調べないと 問題が発生する場合がある ので、MC/DC のテストケースを求める場合は、先頭の式から調べるようにして下さい。

MC/DC に必要なテストケースの数

and 演算子を使った条件式や、and と or 演算子が混在する条件式の場合でも、同様の方法 で、必要最小限のテストケース を求めることが出来ます。証明は省略しますが、MC/DC に 必要なテストケースの数 は、and と or 演算子で連結された式の数を $n$ とすると、n + 1 個 のテストケースが必要となります。従って、この場合のMC/DC によるテストは、複数条件網羅(MCC) によるテストのような 組み合わせ爆発 は 発生しません。

上記の説明を見て、MC/DC のテストケースを用意する手順が複雑で大変だと思った方が多いのではないかと思います。実際に、MC/DC のテストケースを用意するのは大変なのですが、条件式の中で、or 演算子のみ または、and 演算子のみ が使われている場合は、簡単な手順 でテストケースを求めることが できる ので、その方法について紹介します。

残念ながら、or と and 演算子が 混在する場合 は、先程の手順 を使ってテストケースを求める 必要 があります。フリーのものを見つけることはできませんでしたが、そのようなテストケースを求めるツールを利用することが出来るのであれば、利用したほうが良いでしょう。また、組み合わせ爆発が 起きない場合 は 複数条件網羅(MCC) でテストを行ったほうが 簡単な場合 もあります。

参考までに、MC/DC の手順を説明したページのリンクを紹介します。このページの最後に、MC/DC のテストケースを求めるツールが言及されていますが、おそらく有料のツールではないかと思われます。

or 演算子のみで連結された場合

a > 1 or b > 2 or c > 3 は、a > 1、b > 2、c > 3 の 3 つの式 が or 演算子で連結 しています。or 演算子は、すべての式が False の場合は False に、一つ以上の式が True であれば True になるような演算を行うので、この条件式は 値が True になる 式の数 によって、以下の表のように 4 種類に分類できます。

値が True になる式の数	条件式の計算結果
0	False
1	True
2	True
3	True

式の値を 1 つだけ、True から False または、False から True に 変化させた場合 は、値が True になる 式の数 が 1 つだけ増減 します。上記の表から、式の値を 1 つだけ変化 させた場合に、条件式の計算結果が変化 するのは、値が True になる式の数が、「0 から 1 になった場合」と「1 から 0 になった場合」だけです。値が True になる式の数が 2 つ以上 あった場合は、式の値を 1 つだけ変化 させた場合に、条件式の計算結果が 変化する ことは 決してありません。

このことから、以下のことがわかります。

• 値が True になる 式の数が 0 の場合は、どの式の値を変化させても条件式の計算結果に 影響を与える のでテストケースとして 必要 である
• 値が True になる 式の数が 1 の場合は、値が True の式を False に変化 させることで、条件式の計算結果に 影響を与える のでテストケースとして 必要 である
• 値が True になる 式の数が 2 以上 の場合は、どの 1 つの式の値を変化させても、条件式の計算結果に 影響を与えることは無い。従って、そのようなデータは、テストケースとして 必要ではない

従って、a > 1 or b > 2 or c > 3 を MC/DC でテストを行う際に必要となるテストケースは、値が True になる 式の数 が 0 または 1 のデータで、そのテストケースは下記の表の 4 種類 になります。

a > 1	b > 2	c > 3	条件式の値
False	False	False	False
True	False	False	True
False	True	False	True
False	False	True	True

上記の方法で求めたテストケースが、分岐網羅(C1) と 条件網羅(C2) の 両方の性質を満たす ことを示します。

「値が True になる 式の数が 0 の場合は、条件式の値が False」に、「値が True になる 式の数が 1 の場合は、条件式の値が True」になるので、分岐網羅(C1) の性質を満たします。

また、それぞれの式の値 は、テストケースのうちの 1 つだけが True になり、それ以外 のテストケースは False になるので、条件網羅(C2) の性質を満たします。

上記の例では、or 演算子で連結された式の数が 3 つでしたが、式の数が増えた場合 でも 同様の方法 で、式の数 + 1 個 のテストケースを用意することで、MC/DC テストを行うことが出来ます。これは、次に説明する and 演算のみで連結 された場合も 同様 です。

and 演算子のみで連結された場合

and 演算子のみで連結 された条件式の場合も同様です。例えば、a > 1 and b > 2 and c > 3 は、a > 1、b > 2、c > 3 の 3 つの式 が and 演算子で連結 しています。and 演算子は、すべての式が True の場合は True に、一つ以上の式が False であれば False になるような演算を行うので、この条件式は 値が False になる 式の数 によって、以下の表のように 4 種類に分類できます。

値が False になる式の数	条件式の計算結果
0	True
1	False
2	False
3	False

or 演算子の場合と同様の理由で、a > 1 and b > 2 and c > 3 を MC/DC でテストを行う際に必要となるテストケースは、値が False になる 式の数 が 0 または 1 のデータで、そのテストケースは下記の表の 4 種類 になります。

a > 1	b > 2	c > 3	条件式の値
True	True	True	True
False	True	True	False
True	False	True	False
True	True	False	False

経路組み合わせ網羅（path coverage）

条件網羅(C2) では、1 つの条件分岐の中 の組み合わせを考えていましたが、経路組み合わせ網羅では、可能な限り、複数の 条件分岐 の 全ての経路 の 組み合わせ を網羅します。経路（path）を 考慮 するので、英語では、パス・カバレッジと呼びますが、個人的には PC と略して表記するのはあまり見たことがありません。

なお、上記で 可能な限り と書いたのは、条件分岐の条件式によって、通ることが不可能な経路 が存在する 場合がある からです。具体例については、この後で説明します。

経路組み合わせ網羅の目的

関数の中に、複数の条件分岐が記述されている場合、前の条件分岐の処理 が、その後の条件分岐の処理 に 影響を与える 場合があります。そのような場合は、それらの 条件分岐の経路 の 組み合わせ をテストする必要があります。具体例については次で説明します。

経路組み合わせ網羅の例

条件式の中に or や and 演算子が記述されていると複雑になるので、下記の例ではそれらが 記述されていない 条件分岐で説明します。従って、下記の例の場合は、条件網羅(C2) の性質を持つテストに関する内容は出てきません。

下記のプログラムは、以下のような計算を行う calc_a という関数を定義しています。なお、下記のプログラムは、経路組み合わせ網羅が 必要な例 として作ったものなので、行っている計算に 深い意味はありません。

• 仮引数 a の値が 正の場合は、a から 5 を引く
• その結果、a の値が 正の場合は、a に 5 を足す
• a を返り値として返す

def calc_a(a):
    if a > 0:
        a -= 5

    if a > 0:
        a += 5

    return a

最初の if 文の条件分岐だけに注目すると、行われる計算は以下の表のようになります。

a の値	最初の if 文の処理後の a
0 < a	a - 5
a <= 0	a

次の if 文の条件分岐では、a > 0 を調べるので、最初の if 文の処理の結果、a > 0 になる 条件を考える 必要があります。その条件を考えると、以下の表のようになります。

最初の a の値	最初の if 文の処理後の a	次の if 文の処理後の a（返り値）
5 < a	a - 5 （正の値）	a
0 < a <= 5	a - 5 （0 以下）	a - 5
a <= 0	a （0 以下）	a

つまり、この関数は、仮引数 a の値が、0 < a <= 5 の場合は a - 5 を返り値として返し、それ以外の場合 は、a を返すという処理を行います。

この関数に対して 分岐網羅(C1) でテストを行う場合は、下記のような 2 つのテストケースを用意すれば十分です。

	1 つめの a > 0	2 つめの a > 0
テストケース 1	True	True
テストケース 2	False	False

具体的なテストケースとして以下の表のような 2 つのテストケースが考えられます。

	テストデータ（仮引数 a）	期待される値（返り値）
テストケース 1	100	100
テストケース 2	-100	-100

上記のテストケースは、分岐網羅(C1) の条件を満たしていますが、先程の表の 0 <= a < 5 の場合の 経路 のテストが 行われていません 。これが 分岐網羅(C1) の 問題点 です。

経路組み合わせ網羅 の場合は、下記の表のような、条件分岐の 全ての分岐の組み合わせ の経路を通るテストケースを用意します。ただし、実際には、先程の表からわかるように、最初の a がどのような値をとっても、テストケース 3 を満たすような a は 存在しません。従って、実際には下記の表の、テストケース 1、2、4 を満たすような 3 つの a をテストケースとします。

	1 つめの a > 0	2 つめの a > 0	最初の a の値
テストケース 1	True	True	5 < a
テストケース 2	True	False	0 < a <= 5
テストケース 3	False	True	存在しない
テストケース 4	False	False	a <= 0

経路組み合わせ網羅の性質

経路組み合わせ網羅は、最も精度の高いテスト を行うことが出来ますが、それぞれの条件分岐の経路を全て 乗算した数 だけ、テストケースが必要となるので、組み合わせ爆発 が 非常に起きやすい という欠点があります。上記の例では、それぞれの条件式が単純な式でしたが、and や or 演算子が記述されていた場合は、全体のテストケースの数が 膨大な数 になる可能性が高くなります。そのため、テストの 精度が求められない 場合は、経路組み合わせ網羅によるテストは一般的には 行われません。

組み合わせ爆発を防ぐ工夫として、お互いに 影響を与える可能性 がある条件分岐に 絞って、条件式経路組み合わせ網羅を行うという方法もあります。

テストの手法のまとめ

今回の記事で紹介したテストの手法を表にまとめます。なお、テストケースの数と、精度に関しては 目安 なので、状況によっては異なる場合がある点に注意して下さい。

名称	略称	テストケースの数	精度
命令網羅	C0、SC	最小	最小
分岐網羅	C1、DC	小	小
条件網羅	C2、CC	小~中	小
判定条件/条件網羅	CDC	小~中	中
複数条件網羅	MCC	大	大
改良条件判断網羅	MC/DC	中	大
経路組み合わせ網羅	なし	最大	最大

多くの手法を説明しましたが、実際にどれを使うかについては、自分で判断する しかありません。個人的 には、あまり複雑でない 関数の場合は 分岐網羅(C1)、judge メソッドのように、実装したプログラムが正しく動作するか 自信が持てない ような 複雑な関数 の場合は 改良条件判断網羅(MC/DC)、特に高い精度が求められたり、バグがどうしても見つからないような場合は 経路組み合わせ網羅 でテストを行えば良いのではないかと思います。それ以外の手法も 状況に応じて使い分ける ことが出来るようになるのが理想なので、時間に余裕がある方は、次回の記事でテストの具体的な方法を学んだ後で、自分で作った関数に対して、上記の様々な手法でテストを行ってみることをお勧めします。

ただし、時間は有限なので、テストに 時間をかけすぎる のも 良くない と思います。どの程度の関数で、どの程度のテストを行う（もしくは行わない）べきかについては、経験から学ぶ 以外の 方法はない ので、頑張って経験を積んで自分なりのテストの方法を見つけて下さい。

次回の記事について

長くなったので今回の記事はここまでにします。次回の記事では、今回の記事で説明した手法を使って、judge メソッドのテストを行います。

本記事で入力したプログラム

今回の記事には、JupyterLab のファイルと marubatsu_new.py はありません。

次回の記事

1. 具体的な〇×ゲームの局面の数については、〇×ゲームの AI を作る際に計算して示すことにします ↩

2. 中で行われる 具体的な処理を知らずに利用する関数 のようなもののことを、中身が見えない黒い（black）箱（box）に例えて ブラックボックス と呼びます。ホワイトボックスは その反対 で、中で行われる処理を熟知して利用する関数のようなものことを表します ↩