はじめに
本エントリではバンディットアルゴリズムの各手法について,実際のユースケースを想定したシミュレーションを行うことで,それぞれの手法の特徴を把握すること目的とします.
バンディットアルゴリズムについて日本語でよく参照されているのは以下のQiitaの投稿でしょうか.
http://qiita.com/yuku_t/items/6844aac6008911401b19
また以下の資料では各手法の詳細や特徴,簡単なシミュレーションも紹介されています.
http://www.slideshare.net/greenmidori83/ss-28443892
上記の資料の手法の紹介はとてもわかりやすいので本エントリでは手法の紹介は特にしません.
想定するユースケース
あなたは今1万回表示されてクリック率が1.2%出ている広告を1クリック60円で運用しています.
もっとクリックされる広告を見つけるためにいろいろなパターンのバナーを試すことにしました.
10個のバナーを新しく作りました.
このバナーのうち,2つは今のバナーよりクリック率がよく,3つは今の広告と同じで,のこりの5つは今のものよりもクリック率が悪いとします.
- 1.3%が2個
- 1.2%が3個
- 1.1%が3個
- 1.0%が2個
なぜクリック率を上げたいのか
本題とは関係ありませんが,なぜクリック率を上げたいのか,またクリック率が0.1%しか上がらないのに実験をやる意味があるのか?ということについて考えてみましょう.
クリックされるごとに払うお金は変わらないのでクリック率を上げることにそんな意味はないと思われるかもしれません.
しかしその広告を掲載する側から考えればクリック率の低い広告を出すことは売上が下がってしまうため,クリック率が低いとなかなか広告を表示することができなくなってしまいます.
その際よく使われるのはeCPMという指標です.
eCPMはその広告を1000回表示していくらの売上を上げることができるかという指標であり,
クリック率1000クリック単価で求められます.
EPCMが高い広告のほうが表示されやすいため,クリック率を上げることで同じクリック単価でたくさんのユーザを自社のランディングページに誘導することができるようになります.
例えば今回のケースではクリック率1.2%でクリック単価が60円ですので,eCPMは720円です。
ここでクリック率が0.1%上がるとeCPMは780円になります.
そのときクリック単価を56円にしてもeCPMは726円になるため,つまりクリック率が0.1%上がると同じだけのランディングページへの誘導を得るための単価を4円下げることができます.
例えばそのランディングページでの商品の購入が1%で行われるとすると,商品を1つ売るためのコストが400円も下がる事になります.
ケースバイケースではありますが,このようにクリック率を上げることはウェブ広告を通してものを売るために非常に重要な要素になります.
シミュレーション
実装は以下よりお借りしました
EpsilonGreedy, Softmax, UCBについてみていきます
Epsilon Greedy
Epsilon Greedyは一定の確率でいま最良と思っていないような選択肢を選びにいく手法です.
まずは10%程度で探索しにいく形で試してみます.
1000回試行してみましょう.
execfile("core.py")
arm_rates = [0.012, 0.013, 0.013, 0.012, 0.012, 0.012, 0.011, 0.011, 0.011, 0.01, 0.01]
arms = [BernoulliArm(r) for r in arm_rates]
counts = [10000, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
values = [0.012, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
algo1 = EpsilonGreedy(0.1, counts, values)
for t in range(1000):
chosen_arm = algo1.select_arm()
reward = arms[chosen_arm].draw()
algo1.update(chosen_arm, reward)
| base | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 試行回数 | 77 | 109 | 82 | 38 | 38 | 50 | 264 | 205 | 49 | 47 | 41 |
| 評価確率 | 1.2% | 0.9% | 3.7% | 0% | 0% | 2.0% | 2.3% | 2.0% | 0% | 0% | 0% |
11個の選択肢で1,000回程度の試行では全然わかりませんね.
乱数の発生にも依存するのでこの結果はそのとき時によって大きく変わります.
10,000回試行した場合はどうでしょう?
| base | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 試行回数 | 1,321 | 824 | 481 | 623 | 1,827 | 562 | 1,026 | 968 | 452 | 1206 | 710 |
| 評価確率 | 1.2% | 1.2% | 0.6% | 1.2% | 1.3% | 0.7% | 1.2% | 1.1% | 0.9% | 1.2% | 1.3% |
ひどい結果にはなっていないですがいい結果になっているとも言いがたい感じです.
次に探索の度合いを高く50%程度にしてみます.
まずは1,000回
| base | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 試行回数 | 239 | 70 | 40 | 72 | 37 | 44 | 137 | 45 | 52 | 211 | 53 |
| 評価確率 | 1.2% | 1.4% | 0% | 1.4% | 0% | 0% | 1.5% | 0% | 0% | 1.9% | 0% |
心なしかイプシロンが10%の時と比べるとまんべんなく探索されているような状態でしょうか?
次は10,000回
| base | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 試行回数 | 1,035 | 1,915 | 8,120 | 1,046 | 1,026 | 1,104 | 885 | 899 | 1,007 | 1,354 | 1,609 |
| 評価確率 | 1.2% | 1.3% | 1.3% | 1.1% | 1.1% | 1.0% | 0.9% | 1.1% | 1.1% | 0.7% | 1.2% |
一番よいバナーを発見することができましたがまぁたまたまです.
10%の時に比べて他のバナーもまんべんなく試行されていることがみてとれます.
このように試行ごとにばらつきが大きいので,複数回繰り返したepcmの平均で評価しましょう.
eCPMは以下の用に求めます
def calc_ecpm(algo):
total = sum(algo.counts) - 10000
ecpm = 0.0
for idx, count in enumerate(algo.counts):
if idx == 0:
count -= 10000
if count == 0:
continue
ecpm += 1000 * 60 * algo.values[idx] * float(count)/total
return ecpm
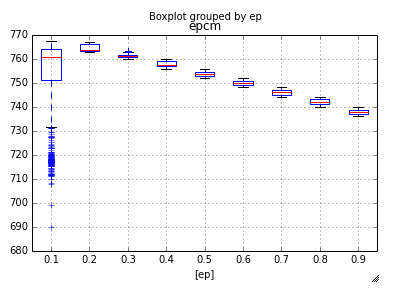
ではパラメータを0.1~0.9の0.1刻みで設定し, 各パラメータについて試行回数10,000回のバンディットを1,000回実行した際のecpmはこのようになります.
def run_eg(ep, counts, values, arms):
algo = EpsilonGreedy(ep, counts, values)
for t in xrange(10000):
chosen_arm = algo.select_arm()
reward = arms[chosen_arm].draw()
algo.update(chosen_arm, reward)
return calc_ecpm(algo)
def run():
data = []
arm_rates = [0.012, 0.013, 0.013, 0.012, 0.012, 0.012, 0.011, 0.011, 0.011, 0.01, 0.01]
arms = [BernoulliArm(r) for r in arm_rates]
counts = [10000, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
values = [0.012, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
for ep in xrange(1, 10):
print ep * 0.1
for _ in xrange(10000):
data.append((ep*0.1, run_eg(ep*0.1, counts, values, arms)))
return pandas.DataFrame(data, columns=['ep', 'epcm'])
result = run()
result.boxplot(by="ep")
イプシロンが小さいと非常にバラつきますね.ただ大きいと得られる成果が小さくなるみたいです.
また元々のecpmである720を基本的には上回ることもわかりました.このようなシンプルなアルゴリズムでも十分に有益な結果は得られるようです.
SoftMax
Softmaxのパラメータはtauです.小さければ小さいほどすでに計算した値を信用するということになります.
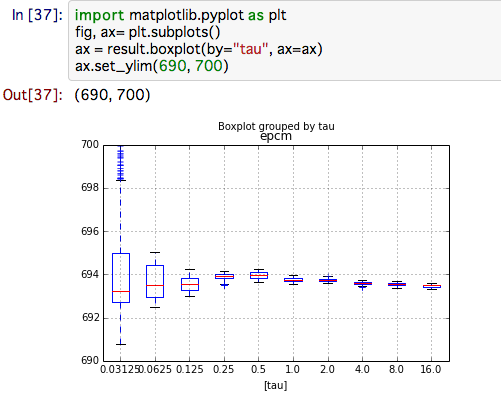
こちらは2^-5 ~ 2^5までのパラメータをそれぞれ1,000回ずつ試行します
def run_sm(tau, counts, values, arms):
algo = Softmax(tau, counts, values)
for t in xrange(10000):
chosen_arm = algo.select_arm()
reward = arms[chosen_arm].draw()
algo.update(chosen_arm, reward)
return calc_epcm(algo)
def run():
data = []
arm_rates = [0.012, 0.013, 0.013, 0.012, 0.012, 0.012, 0.011, 0.011, 0.011, 0.01, 0.01]
arms = [BernoulliArm(r) for r in arm_rates]
counts = [10000, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
values = [0.012, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
for i in xrange(10):
tau = 2**(i - 5)
print tau
for _ in xrange(10000):
data.append((tau, run_sm(tau, counts, values, arms)))
return pandas.DataFrame(data, columns=['tau', 'epcm'])
result = run()
result.boxplot(by="tau")
なんと普通にやるより悪い結果が出てしまいました!
softmaxは常に一定の確率で悪い値を引き続けるからですね.
softmaxを使うときは悪い選択肢を切り捨てることを早くやっていく必要がありそうです.
UCB
最後にUCBです
UCBにはパラメータがないのでそのままやります
def run_ucb(counts, values, arms):
algo = UCB1(counts, values)
for t in xrange(10000):
chosen_arm = algo.select_arm()
reward = arms[chosen_arm].draw()
algo.update(chosen_arm, reward)
return calc_epcm(algo)
def run():
data = []
arm_rates = [0.012, 0.013, 0.013, 0.012, 0.012, 0.012, 0.011, 0.011, 0.011, 0.01, 0.01]
arms = [BernoulliArm(r) for r in arm_rates]
counts = [10000, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
values = [0.012, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
for _ in xrange(10000):
data.append(run_ucb(counts, values, arms))
return pandas.DataFrame(data, columns=['epcm'])
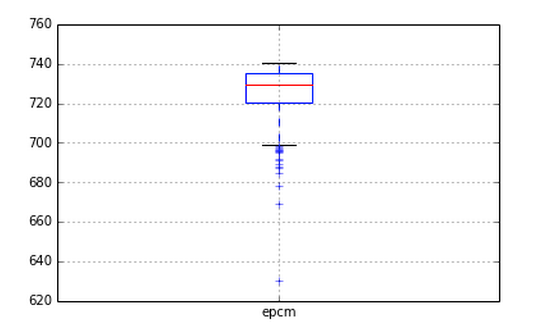
result = run()
epcmを下げないで探索ができていることがわかる.
EpsilonGreedyと比較すると低くなるが,おそらくこの辺りは探索スピードとのトレードオフになりそう.
それぞれの手法の比較とか考察とか
あとで書きたい。あとA/Bテストとの比較もしたい。
まとめ
別にこのエントリでどの手法がいいとかそういうことが言えるわけではなく,
もっとユースケースを突き詰めるならば考えなければならないことはたくさんあるとは思いますが,
バンディットアルゴリズムとはどういうものなのかのなんとなくの理解につながればと思います.
バンディットアルゴリズムは、これまでに得たデータ資産を活用しながら探索ができることが特徴で,
そのメリットの一つとしては探索によってeCPMのような重要な指標を下げて事業を危険に晒すリスクを軽減できることにあるのかなと思っています。
なのであえて、正しい選択ができたかということよりも事前にデータ資産があるときにどのような効用を得ることができるのかという検証がしたくてこのようなシミュレーションをしてみました.
皆様のご参考になれば幸いです.
そしてご意見あれば伺ってみたいのでお気軽にコメントください!