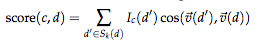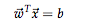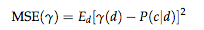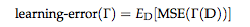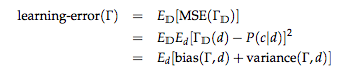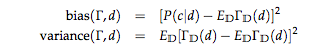Introduction to Information Retrieval の14章輪読用
Gunosy研究会 #31 の資料です
Introduction
ナイーブベイズでは用語を用語列か2値ベクトルで表現した
本章ではベクトル空間モデルを用いて文書を表現し,テキストを分類する.
基本的な考え方
- ベクトル空間モデルでは各用語に対して1つの実数値の要素をもつベクトルとして各文書を表現する
- 通常TF-IDFを用いる
- R^|V| のベクトルとして表現される
- ベクトル空間分類は連続性仮説(contiguity hypothesis)の元に成り立つ
- 同じクラスの文書は連続した領域を形成し,他のクラスの領域とは重なり合わない.
- 連続領域に写像されるかどうかは文書の表現方法による
- 重み付け・ストップワードなど
- ex: "グループによって書かれた文書"と"個人によって書かれた文書"を区別したいケース
- 一人称(I)が頻繁に出現するかどうかで判別可能
- 一般的なストップワード処理を行うと判別できない
- 多くの文書分類器は線形分類器(liner classifier)としてみなすことができる
- 特徴空間を線形の決定超平面(decision hyperplane)で分離された領域に分割する
14.1 文書の分類とベクトル空間での関係性の指標
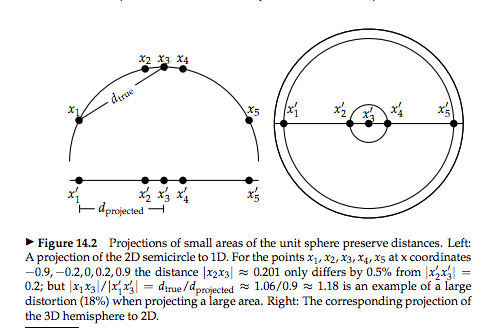
文書ベクトルは長さで正規化された超球(hypersphere)の表面を指す単位ベクトルである
- 超球の平面の小さな部分に制限して適切な射影を選べば,球場の表面と射影平面での距離は近似的に同じである.
- 大きな部分を射影する場合は大きなねじれが起きる
ベクトル空間分類器の決定は距離の概念に基づく
- 本章ではユーグリッド距離を用いる
- 長さで正規化したベクトルに対してはコサイン類似度(cosine similarity)とユーグリッド距離の間には直接的な対応がある
=> 距離か類似度かは大きな問題にならない
重心・平均ベクトルも重要な働きをする
- 重心・平均ベクトルは正規化されていないため,内積・類似度・ユーグリッド距離のどれも異なる挙動を示す
- 小さな局所的な領域を考慮することで,これら3つの挙動を似たものにすることができる
14.2 ロッキオ分類
ベクトル空間分類の目的
各ベクトルをそれぞれのクラスに分類する良い境界(決定境界と呼ぶ)を計算すること
- 良い境界: 訓練中(境界を決定している間)に見なかったデータを正しいクラスに分類できること
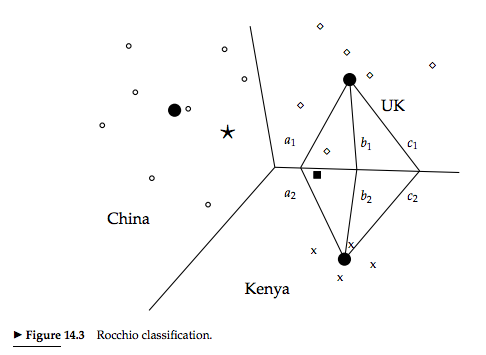
ロッキオ分類
重心を用いて境界を決定する,ベクトル空間分類において最もよく知られた方法
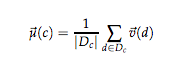
D_c : クラスがcである文書集合
v(d): 文書dの正規化されたベクトル
ロッキオ分類におけるクラス間の境界は2つの重心から等距離にある点の集合であり,この点集合は常に1本の線である.
M次元空間での1本の線は以下の式で一般化される.
線: 平面を2つに分ける
平面: 3次元空間を2つに分ける
超平面: それより高次の空間を2つの分ける
=> ロッキオ分類は超平面である
ロッキオ分類の分類規則
ベクトルが最も近い重心を決定し,その重心のクラスを割り当てる.
"最も近い"の基準は問題により,ユーグリッド距離だったり,コサイン類似度だったりする
これらの基準の違いにより異なる分類決定を行うことがある
ロッキオ分類の性質
ロッキオの適合フィードバック(9.1.1 158P)の一つの形である
=> ロッキオの適合フィードバックは関連文書と非関連文書の重心をとってクエリベクトルを変更している
ロッキオ分類のクラスは半径の似た近似球でなくてはならない
=> クラスにおける点の分布の傾向を無視して重心の距離のみを考えるため.
ロッキオは複合的なクラスをしばしば間違って分類する
=> 球状の仮定が守られていない
2クラス分類
2クラス分類は空間の小さい領域を占める目標クラスとそれ以外の補集合を区別するというタスクになる
=>両方のクラスの重心を考えると多くの偽陽性を引き起こす(補集合が近似球にならないので重心が定まらない)
計算量評価
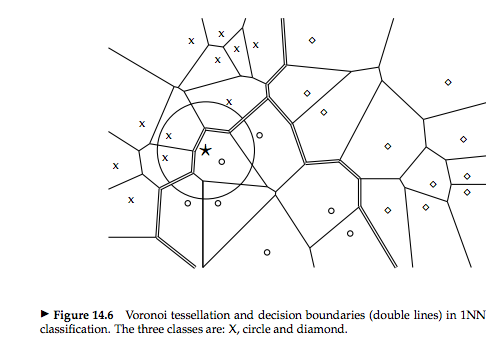
14.3 k最近傍法(k-nearest neibor method)
kNN分類法とも呼ばれる.ここでkは手法のパラメータである.
仮説: 文書dはdを取り巻く局所的な領域にある訓練文書と同じラベルを持つ
決定境界を局所的に決定するため,非球や分離されているものや非定形のクラスをうまく扱うことができる.
kNN分類法の分類方法
1NN => 各文書に一番近いクラスを割り当てる
kNN => k個の最近傍の中で一番多いクラスを割り当てる
1NNはあまり頑健ではない
=> 最も近い文書のラベルが間違っているかも知れないし,特殊なものかもしれない
kNN分類法の確率的解釈
文書がクラスcに所属する確率をk最近傍のクラスcの割合で評価することができる.
パラメータkの決定方法
経験、あるいは以前からの分類問題の知識に基づいて選ばれる
引き分けの場合を減らすために奇数が望ましい.
一般的にはk=3, 5が用いられるが,50 ~ 100といった大きな値が用いられることもある.
別の方法として,訓練集合を用いて最適なkを決定するという方法もある
=> 研究的にはこっちがメジャーっていうか必須な気がする…
コサイン類似度を用いたクラスの決定
k最近傍の投票(votes) (kの中でどのクラスに属するかを決定すること)をコサイン類似度で重み付けすることもできる
S_k: dの最近某集合
I_c:(d): dがクラスcにあるときに1,そうでない時に0をとる
14.3.1 計算時間量とk最近傍
トークン化の様な前処理とkの値を決める以外に訓練は必要ない
テスト時間はテスト集合に対して線形であり,クラス数とは独立である
=>クラス数が多い場合には利点がある.
kNN分類の特性
ナイーブベイズやロッキオ分布のようにパラメータ推定を行わない
=> メモリに基づく学習(memory-based learning), 事例に基づく学習(instance-based learning)と呼ばれる
=> 機械学習では訓練データは多ければ多いほど望ましいが,kNNでは逆に非効率である
14.4 線形分類器 vs 非線形分類器
議論の簡単化のために2クラス分類器のみを議論する.
線形分類器
特徴の線形結合を閾値と比較することで所属するクラスを決定する2クラス分類器
超平面 (式14.3)
クラスの割り当て
wx > b : c
wx <= b : c¬
wとbを訓練データから決定し,超平面を決定してテストデータにクラスを割り当てる
線形分離可能
2つのクラスを完璧に分類する超平面があるのなら,その2つのクラスは線形分離可能と呼ばれる.
多くの場合決定超平面は無限に存在するため,選択基準が必要である.
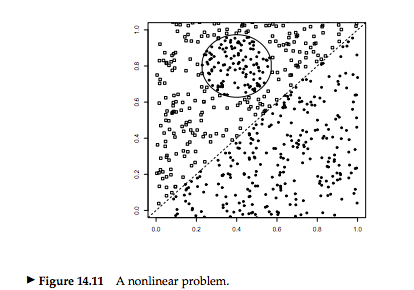
非線形分類器
kNNは非線形分類器である
飛び地
このようなクラス境界が線形超平面でうまく禁じできない場合に場合に訓練データが十分あれば,非線形分類器は有効である.
14.5 クラス数が2より多い分類
クラス数J > 2の場合
クラスが互いに排他的か否かで使用する手法が異なる
排他的でない場合
同時にいくつかのクラスに所属したり,ひとつのクラスに所属したり,どこクラスにも所属しないkとおができる
=> any-of, multilabel, multivalue classificationと呼ばれる
分類方法
J個の分類器をを学習し,各々の分類器がc, c¬のどちらかを返す.
排他的な場合
一つのクラスにしか所属することができない
=> one-of classification, multinomial, polytomous, multiclass, single-label classification
=> kNNは排他的な分類器である
J個の超平面は空間をJ個の異なる空間に分割しない(図14.12)
分類方法
クラスをランク付け評価し,最も上位に評価されたクラスを選ぶ
=> あるクラスの分離線に近い文書は間違う可能性が高いため,J個の線形分離における距離からランク付けをする等.
14.6 バイアス-バリアントレードオフ
分類器の評価
文書がクラスに属しているかを分類器がどの程度うまく評価するかをみる.
平均二乗誤差(Mean Squared Error, MSE )
P(c|d) : Bug of wordsモデルでは異なる文書でも同じ文書表現で表すことがある
MSE(γ)が最小であれば分類器γが最良
学習法の評価
学習法: 訓練集合Dを受け取って分類器γを返す
極小のMSEを持つ分類器γを学ぶ学習法Γをみつける
dとDは独立
=> Dはdのラベル付き事例を含まない
バイアス(bias)
cでのdである真の条件付き確率と訓練集合上で平均化した学習付分類器の予測Γ_D(d)間の平方誤差
=> 学習法が一貫して誤った分類器を生み出すならバイアスは大きい
=> (1) 分類器が一貫して正しい
=> (2) 誤った訓練集合によって誤った予測を生む
=> (3) 誤った訓練集合によってある文書がpositiveだったりnegativeだったりするが,それを平均すると0になる
=> (1) ~ (3)のいずれかが成立すればバイアスは小さい
線形と非線形
線形分類器を非線形問題に適用した際には高いバイアスを生む
=> 問題を線形か非線形か知っているか否かというdomain knowledgeが作用する
非線形分類器は低いバイアスを持つ
バリアンス(variance)
Γ_{D}(d)とその平均E_{D}Γ_{D}(d)の間の平均平方誤差
=> 学習された分類器の予想の多様性
=> 異なる訓練集合Dがとても異なる分類器Γ_{D}を生み出す -> バリアンスは大きい
=> 訓練集合の違いが分類器にもたらす影響は小さい -> バリアンスは小さい
その決定がどれだけ一貫しているかを測る => 正確さを測るわけではない
高いバリアンスを持つ手法はover-fittingしやすい
線形と非線形
線形学習法はランダムに選ばれた訓練集合が似た決定超平面を生み出す
=> バリアンスが小さい
kNNのような非線形学習法は高いバリアンスをもつ
=> ノイズ文書によって結果の変動が大きくなる
トレードオフ
学習誤差を最小化することが目的
=> 学習誤差 = バイアス + バリアンス
=> バイアス-バリアンストレードオフ
良い分類器の多くは線形である
- 線形SVM
- ロジスティクス回帰
- 正規線形回帰
テキスト分類の典型的なクラスは複雑で線形でモデル化出来ないように見えるが,
高次元空間では線形分離の可能性は急速に増える.
非線形分類器は超平面より複雑な決定境界をモデル化することができるが,
ノイズに敏感であり,訓練集合が大きい時にはよりよく働くがそれは全ての場合ではない.