概要
- julialang で Mamba.jl のサンプルを動かします
- julia v0.6 を前提にします
- ubuntu 16.04を前提にします
- tutorial を実行した jupyter notebook はこちら
Mamba.jl 導入
Mamba.jl の Tutorialを追いかけます
ここからチュートリアル全体のコードをダウンロード可能です
ベイズ線形回帰モデル
BUGS 0.5 マニュアル[89]からベイズ単純線形回帰モデルを例にパッケージの特徴を説明します。
この例は、観測された${{\vec{x}}=(1,2,3,4,5)^\top}$と${{\vec{y}} =(1,3,3,3,5)^\top}$の直線的関係( regression relationship )を説明します。
yは次から得られます。
\begin{aligned}
\vec{y} &\sim \text{Normal}(\vec{\mu},\sigma^2\bf{I})\\
\vec{\mu} &= \bf{X}\vec{\beta}
\end{aligned}
事前分布の定義 (prior distribution specifications) は以下です。
\begin{aligned}
\vec{\beta} &\sim \text{Normal}\left(\vec{\mu}_\pi=
\begin{bmatrix}
0 \\
0
\end{bmatrix}
, {\bf{\Sigma}}_\pi=
\begin{bmatrix}
1000 & 0 \\
0 & 1000
\end{bmatrix}
\right)\\
\sigma^2 &\sim \text{InverseGamma}(\alpha_\pi=0.001,\beta_\pi=0.001)
\end{aligned}
$\vec{\beta}=(\beta_0,\beta_1)^T$であり、
第１列に切片ベクトルをもち、第２列に$\vec{x}$をもつ行列$\bf{X}$を考えます
最も関心のある点は、それぞれの事後分布を元にして、$\beta_0,\beta_1,\sigma^2$のパラメータを推論することです
この例についての計算上の考慮は、同時事後確率は以下の比例定数から導かれまた、正規分布の形をしていないために、推論が直接的には得られないということです。
\begin{aligned}
p(\vec{\beta},\sigma^2|\vec{y}) &\propto p(\vec{y}|\vec{\beta},\sigma^2)p(\vec{\beta})p(\sigma^2)\\
&\propto (\sigma^2)^{-\frac{n}{2}} exp \left\{-\frac{1}{2\sigma^2}(\vec{y}-{\bf{X}}\vec{\beta})^T(\vec{y}-{\bf{X}}\vec{\beta}) \right\}\\
&\quad \times exp \left\{-\frac{1}{2}(\vec{\beta}-\vec{\mu_\pi})^T{\Sigma}_{\pi}^{-1}(\vec{\beta}-\vec{\mu_\pi})\right\}(\sigma^2)^{-\alpha_{\pi}-1}exp \left\{ -{\frac{\beta_\pi}{\sigma^2}} \right\}
\end{aligned}
一般的な代替法は、MCMC法を用いて事後分布からシミュレートされたパラメータ値に基づいて近似推論を行うことです。
モデル記述
ノード
Mamba パッケージにおいて、ノードとして参照されるベイジアンモデル記述用の用語が現れます。
ノードは３つのタイプに分けられます。
- ストキャスティクスノード:全ての尤度や、事前分布の定義 (prior distribution specifications) についてのモデル用語です。線形回帰モデルでは$\vec{y},\vec{\beta},\sigma^2$がストキャスティクスノードにあたります。
- ロジカルノード:他のノードから計算で求められる$\vec{\mu}$のようなノードです。
- インプットノード:他の全てのモデル$(\bf{X})$であり、分析において固定された量とみなされます。
$\vec{y}$ノードは、分布形式の定義 (distributional specification) であり、固定された値でもあります。
Mamba においては、分布形式の定義 (distributional specification) により、ストキャスティクスノードとして指定されています。
これは、目的ベクトルに欠損値があった場合など、観測された要素と観測されなかった要素の混合の場合などに分布形式の定義 (distributional specification) のモデルが可能になります。
モデルの実装は、Mamba が提供するコンストラクタ Stochastic, Logical を使い、ストキャスティックノードとロジカルノードをインスタンス化することから始まります。
モデルのストキャスティックノードとロジカルノードは、 Model コンストラクタから よばれ、定義されます。
Model コンストラクタは形式的に名前をノードに定義し割り当てます。
LogicalノードとStocasticノードが渡される定義式の左辺にユーザ指定の名前を与えます。
using Mamba
## Model 記述
model = Model(
y = Stochastic(1,
(mu, s2) -> MvNormal(mu, sqrt(s2)),
false
),
mu = Logical(1,
(xmat, beta) -> xmat * beta,
false
),
beta = Stochastic(1,
() -> MvNormal(2, sqrt(1000))
),
s2 = Stochastic(
() -> InverseGamma(0.001, 0.001)
)
)
Stochaticコンストラクタの最初の引数である一桁の整数値は、ノードが引数によって指定された次元の配列であることをあらわします。
この整数値を省くことで、スカラーノードであることを暗黙的に表します。
その次の引数は、有効な julia コードを含んだ関数です。
引数にしている関数は、ノードが依存する入力を引数として取ります。ストキャスティックノードの場合、distribution オブジェクトまたは Distributions パッケージ[2]と互換性のあるオブジェクトの配列を返すように定義する必要があります。
このようなオブジェクトは、ノードの確率分布の定義(nodes’ distributional specifications)を表します。
MCMCシミュレーション中にノードの値をモニタ（保存）する必要があるかどうかを示すために、関数の後のオプションに boolean 引数を指定できます（デフォルトではtrue）。
Stochastic 関数は、ノードの次元数を受け取れる単一の distribution オブジェクトを返すか、ノードと同じ次元の（単変量または多変量） distribution オブジェクトの配列を返します。
beta ノードの事前分布について、等価な代替の書式の例を以下に示します。
# ケース1：独立の共分散行列を持つ多変量正規分布
beta = Stochastic(1,
() -> MvNormal(2, sqrt(1000))
)
# ケース2：単変量の正規分布
beta = Stochastic(1,
() -> Normal(0, sqrt(1000))
)
# ケース3：単変量正規分布の配列
beta = Stochastic(1,
() -> UnivariateDistribution[Normal(0, sqrt(1000)), Normal(0, sqrt(1000))]
)
# ケース4：単変量正規分布の配列
beta = Stochastic(1,
() -> UnivariateDistribution[Normal(0, sqrt(1000)) for i in 1:2]
)
ケース1は、 Distributions パッケージで使用可能な多変量正規分布の1つであり、モデル実装例で使用されている定義です。
ケース2では、1つの単変量正規分布が、betaのすべての要素に対して同じ型の独立事前分布を意味するように指定されています。
ケース3および4は、beta の各要素に対して、単変量を明示的に指定し、事前分布間の差異の可能性を考慮に入れます。両方とも Distribution オブジェクトの配列を返します。最後のケースでは、配列要素の指定を自動化しています。
つまり、yおよびbetaはストキャスティクスベクトルであり、s2 はストキャクスティクススカラーであり、mu はロジカルベクトルです。
今回のモデルはmuを使用しないで実装できた可能性があることに注意してください。
主にロジカルノードの使用方法を示すために、今回のモデルに含まれています。
最後に、y と mu ノードがモニタされていないことに注意してください。
サンプリングスキーマ
このパッケージは、ストキャスティクスノードをサンプリングする為の柔軟なスキーマ実装を用意しています。
ノードの任意のブロック化と、ブロック特定のサンプラ指定がサポートされています。
さらに、このパッケージから提供されるサンプラや、ユーザによって定義されるサンプラ、または他のパッケージから利用可能なサンプラを用いて、ノードのブロック更新を行うことができます。
スキーマは Sampler オブジェクトのベクトル型として指定されます。
コンストラクタは、アダプティブメトロポリス、NUTS（No-U-Turn）、スライスサンプリングなどの一般的なサンプリングアルゴリズムに対応しています。
スキーマ例を以下に示します。
一例目は、NUTSを beta のサンプリングに用い、スライスサンプリングを s2 のサンプリングに用います。
二例目のスキーマでは、二つのノードはともにブロック化され、NUTSによって同時にサンプリングされます。
## ハイブリッド No-U-Turn と スライスサンプリングのスキーマ例
scheme1 = [NUTS(:beta),
Slice(:s2, 3.0)]
## No-U-Turn サンプリングのスキーマ例
scheme2 = [NUTS([:beta, :s2])]
さらに、ユーザは汎用 Sampler コンストラクタを使用して独自のサンプラを自由に作成できます。
このコンストラクタは、いくつかのノードの完全条件付き分布 (full conditional distributions) が標準正規分布であり、また直接サンプリングすることができるという設定の場合、特に有用です。
今例のうち、$\vec{\beta}$の完全条件式 (full conditional) の場合であり、次のように書くことができます。
\begin{aligned}
p(\vec{\beta}|\sigma^2,\vec{y}) &\propto p(\vec{y}|\vec{\beta},\sigma^2)p(\vec{\beta})\\
&\propto exp \left\{-\frac{1}{2}(\vec{\beta}-\vec{\mu_\pi})^T{\Sigma}^{-1}(\vec{\beta}-\vec{\mu_\pi})\right\}
\end{aligned}
このうち
$\Sigma=\left( \frac{1}{\sigma^2}{\bf{X}}^T{\bf{X}} + {\Sigma}_{\pi}^{-1} \right)^{-1}$
であり、
${\vec{\mu}}=\Sigma \left( \frac{1}{\sigma^2}{\bf{X}}^T\vec{y} + {\Sigma}_{\pi}^{-1} {\vec{\mu}}\right)$
です。これは多変量正規分布と認められます。同様に、
\begin{aligned}
p(\sigma^2|\vec{\beta},\vec{y}) &\propto p(\vec{y}|\vec{\beta},\sigma^2)p({\sigma^2})\\
&\propto (\sigma^2)^{-\left({\frac{n}{2}+{\alpha}_{\pi}}\right)-1} exp \left\{-\frac{1}{\sigma^2}\left( \frac{1}{2} (\vec{y}-{\bf{X}}\vec{\beta})^T(\vec{y}-\bf{X}\vec{\beta})+\beta_{\pi} \right) \right\}
\end{aligned}
これは、
${\frac{n}{2}+{\alpha}_{\pi}}$
という形状と
$(\vec{y}-{\bf{X}}\vec{\beta})^T(\vec{y}-\bf{X}\vec{\beta})+\beta_{\pi}$
というスケールパラメータを持つ逆ガンマ分布です。
これらの完全条件式 (full conditional) から描画を生成するためのユーザ定義のサンプリング方式を以下に示します。
別の例は、複数のノードのサンプリングのための Pollution例 に示されています。
## ユーザ定義サンプラ
Gibbs_beta = Sampler([:beta],
(beta, s2, xmat, y) ->
begin
beta_mean = mean(beta.distr)
beta_invcov = invcov(beta.distr)
Sigma = inv(Symmetric(xmat' * xmat / s2 + beta_invcov))
mu = Sigma * (xmat' * y / s2 + beta_invcov * beta_mean)
rand(MvNormal(mu, Sigma))
end
)
Gibbs_s2 = Sampler([:s2],
(mu, s2, y) ->
begin
a = length(y) / 2.0 + shape(s2.distr)
b = sumabs2(y - mu) / 2.0 + scale(s2.distr)
rand(InverseGamma(a, b))
end
)
## ユーザ定義サンプリングスキーマ
scheme3 = [Gibbs_beta, Gibbs_s2]
これらのサンプラでは、ストキャスティクスノード beta, s2 のそれぞれの事前分布 MvNormal(2, sqrt(1000)) とInverseGamma(0.001, 0.001) は distr フィールドを介して直接アクセスされています。
beta.distr および s2.distr によって返された Distributions オブジェクトの機能は、そのパッケージで定義されたメソッド関数または独自のフィールドで抽出できます。
例えばメソッド関数 mean(beta.distr) と invcov(beta.distr) は、それぞれ beta の事前分布の平均ベクトルと逆共分散行列を抽出しています。
それに対して、 shape(s2.distr) と scale(s2.distr) は、 s2 の事前分布、逆ガンマ分布のフィールドから形状とスケールパラメータを抽出します。
Distributions のメソッド関数は、Distributions.jl パッケージのドキュメントにあります。 一方、distr フィールドについてはソースコード内にあります。
## サンプリングスキーマ割り当て
setsamplers!(model, scheme1)
あるいは、事前に定義されたスキーマを、モデル実装時に samplers 引数の値として Model コンストラクタに渡すことができます。
有向非巡回グラフ
Model によって作成された内部構造の1つに、モデルノードとその関連付けのグラフ表現があります。
グラフは内部的に LightGraphs パッケージで管理されています[11]。
OpenBUGS、JAGS、および他の BUGS言語 クローンと同様に、Mamba はノードが有向非循環グラフ（directed acyclic graph:DAG）を形成するモデルに適しています。
DAGは、ノードが有向辺によって接続され、ノードが自身へのループバックする経路を持たないグラフです。
統計的モデルにおいて、有向辺は親ノードからそれに依存する子ノードを指します。
したがって、子ノードは、その親が与えられたとすると、他の全てのノードから独立しています。
Model のDAG表現は、コマンドラインから出力することも、Graphviz ソフトウェアで表示できる形式で外部ファイルに保存することもできます。
## ノードのグラフ表現
>>> draw(model)
digraph MambaModel {
"mu" [shape="diamond", fillcolor="gray85", style="filled"];
"mu" -> "y";
"xmat" [shape="box", fillcolor="gray85", style="filled"];
"xmat" -> "mu";
"beta" [shape="ellipse"];
"beta" -> "mu";
"s2" [shape="ellipse"];
"s2" -> "y";
"y" [shape="ellipse", fillcolor="gray85", style="filled"];
}
>>> draw(model, filename="lineDAG.dot")
出力または保存されたアウトプットのいずれかを Graphviz ソフトウェアに渡して、モデルの視覚的表現をプロットすることができます。
julia が IJulia [50]のようなインライングラフィックスをサポートするフロントエンドで使用されていて、GraphViz julia パッケージ[26]がインストールされている場合、次のコードは自動的にグラフをプロットします。
using GraphViz
>>> display(Graph(graph2dot(model)))
回帰モデルの生成されたDAGプロットを、下の図に示します。
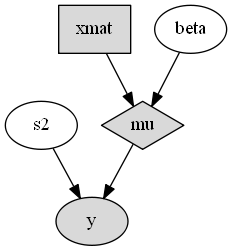今例における回帰モデルノードの有向非巡回グラフ表現
ストキャスティクスノードは楕円形、ロジカルノードは菱形、およびインプットノードは長方形でおのおの表されます。
MCMCシミュレーションでモニタされていないノードは、グレーのノードとして表されます。
DAGは、モデル仕様が意図されたものであることを視覚的にチェックするだけでなく、ノードの関係が非巡回的であることを内部的にチェックするためにも使用されます。
MCMC シミュレーション
データ
例えば、観測された ($\vec{\bf{x}}, {\vec{\bf{y}}}$) は、下記のコードブロックで定義される julia ディクショナリ型に保持されます。
プレディクタベクトル :x とレスポンスベクトル :y が含まれ、モデル行列 $\bf{X}$ に対応するデザイン行列 :xmat も定義されています。
## データ
line = Dict{Symbol, Any}(
:x => [1, 2, 3, 4, 5],
:y => [1, 3, 3, 3, 5]
)
line[:xmat] = [ones(5) line[:x]]
初期値
次に、全てのストキャスティクスノードの初期値を含む julia のディクショナリ型ベクトルを作成する必要があります。
ディクショナリ型の key はノード名と一致しなければならず、その値は、ノードの構造タイプと同じ要素を持つベクトルである必要があります。
回帰モデル例の初期値の３組は、下記のコードから作成されます。
## 初期値
inits = [
Dict{Symbol, Any}(
:y => line[:y],
:beta => rand(Normal(0, 1), 2),
:s2 => rand(Gamma(1, 1))
)
for i in 1:3
]
y の初期値は、観測されたレスポンスベクトルです。
同様に、このノードは、先に定義したサンプリング方式では更新されず、従って、MCMCシミュレーション全体を通してその初期値を保持します。
beta の初期値は正規分布から、s2 の初期値はガンマ分布から生成されます。
MCMC エンジン
モデルノードの宣言されたセットの事後分布から試行するMCMCシミュレーションとサンプリングスキーマは、mcmc() 関数を使用して実行されます。
以下に示すように、最初の3つの引数は、 Model オブジェクト、インプットノードの値のディクショナリ型、および初期値のディクショナリ型ベクトルです。
各シミュレーション実行で生成される試行回数は、第4引数として与えます。
残りの引数について、 burnin は収束させるために破棄する初期試行回数の値です。
thin には出力に保持される試行間の間隔を指定します。
chains にはシミュレータを実行する回数を指定します。
結果は、事後分布推論のためのメソッドが定義された Chains オブジェクトとして返されます。
## MCMC シミュレーション
setsamplers!(model, scheme1)
sim1 = mcmc(model, line, inits, 10000, burnin=250, thin=2, chains=3)
setsamplers!(model, scheme2)
sim2 = mcmc(model, line, inits, 10000, burnin=250, thin=2, chains=3)
setsamplers!(model, scheme3)
sim3 = mcmc(model, line, inits, 10000, burnin=250, thin=2, chains=3)
並列計算
julia がマルチプロセッサ・システム上で、かつマルチプロセッサ・モードで実行されている場合は、複数のチェーンのシミュレーションが自動的に並列して実行されます。
マルチプロセッサモードはコマンドライン引数 julia -p nで開始することができます。ここでの n は利用可能なプロセッサの数です。
詳細は julia ドキュメントの parallel computing を参照してください。
事後分布推論
収束診断
シミュレートされた描画と事後分布との収束を、MCMC出力チェックを実行し評価する必要があります。
チェックはさまざまな方法で実行できます。
Gelman、Rubin、Brooks の診断[33] [12]は、事後平均推定の収束を評価するための1つの方法です。
診断の潜在的な縮尺係数（PSRF : potential scale reduction factor）の値が、１に近いとき収束の可能性を示しています。
経験則として、PSRFの97.5パーセンタイルが1.2より大きい場合、収束は棄却されます。
>>> gelmandiag(sim1, mpsrf=true, transform=true) |> showall
Gelman, Rubin, and Brooks Diagnostic:
PSRF 97.5%
beta[1] 1.009 1.010
beta[2] 1.009 1.010
s2 1.008 1.016
Multivariate 1.006 NaN
Geweke の診断[37]では、事後平均推定の非収束性がテストされています。
この非収束性診断は、各チェーン固有のp値を表示します。
以下の、第１チェーンの s2 について得られた結果のように、有意なp値については収束性が棄却されます。
>>> gewekediag(sim1) |> showall
Geweke Diagnostic:
First Window Fraction = 0.1
Second Window Fraction = 0.5
Z-score p-value
beta[1] 1.237 0.2162
beta[2] -1.568 0.1168
s2 1.710 0.0872
Z-score p-value
beta[1] -1.457 0.1452
beta[2] 1.752 0.0797
s2 -1.428 0.1534
Z-score p-value
beta[1] 0.550 0.5824
beta[2] -0.440 0.6597
s2 0.583 0.5596
HeidelbergerとWelch の診断[47]では、非収束性（非定常性）のテストと、平均に対する推定区間の半値幅の比率が目標比率内にあるかどうかのテストを行います。
有意なp値( この例は $\alpha=0.05$)の結果ついて定常性は棄却されます（ Stationarity値が 0）。
半値幅テストは、第２チェーンと第３チェーンの s2 と beta[1] の場合のように、観測された（半値幅／平均）比率が目標とする半値幅比(Target Halfwidth Ratio) ( この例は 0.1 )よりも大きい場合は棄却されます（ Test値が 0）。
>>> heideldiag(sim1) |> showall
Heidelberger and Welch Diagnostic:
Target Halfwidth Ratio = 0.1
Alpha = 0.05
Burn-in Stationarity p-value Mean Halfwidth Test
beta[1] 251 1 0.0680 0.57366275 0.053311283 1
beta[2] 738 1 0.0677 0.81285744 0.015404173 1
s2 738 1 0.0700 1.00825202 0.094300432 1
Burn-in Stationarity p-value Mean Halfwidth Test
beta[1] 251 1 0.1356 0.6293320 0.065092099 0
beta[2] 251 1 0.0711 0.7934633 0.019215278 1
s2 251 1 0.4435 1.4635400 0.588158612 0
Burn-in Stationarity p-value Mean Halfwidth Test
beta[1] 251 1 0.0515 0.5883602 0.058928034 0
beta[2] 1225 1 0.1479 0.8086080 0.018478999 1
s2 251 1 0.6664 0.9942853 0.127959523 0
RafteryとLewisの診断 [74] [75]は、希望の accuracy の範囲内( Accuracy (r) = 0.005)で特定の分位数を推定するために必要な itelation 回数を決定するために使用されます。
例えば、0.025 分位 ( Quantile (q) = 0.025)を推定するために必要とされる itelation の総回数、破棄される burn-in 区間の数、thin 間隔が以下の結果で示されます。上記の推定累積確率は、 確率 0.95 ( Probability (s) = 0.95)で 0.025±0.005 以内です。
>>> rafterydiag(sim1) |> showall
Raftery and Lewis Diagnostic:
Quantile (q) = 0.025
Accuracy (r) = 0.005
Probability (s) = 0.95
Thinning Burn-in Total Nmin Dependence Factor
beta[1] 2 267 17897 3746 4.7776295
beta[2] 2 267 17897 3746 4.7776295
s2 2 257 8689 3746 2.3195408
Thinning Burn-in Total Nmin Dependence Factor
beta[1] 4 271 2.1759x104 3746 5.8085958
beta[2] 4 275 2.8795x104 3746 7.6868660
s2 2 257 8.3450x103 3746 2.2277096
Thinning Burn-in Total Nmin Dependence Factor
beta[1] 2 269 2.0647x104 3746 5.5117459
beta[2] 2 263 1.4523x104 3746 3.8769354
s2 2 255 7.8770x103 3746 2.1027763
診断機能の詳細については、Convergence Diagnostics セクションを参照してください。
事後分布要約
収束性を評価した後、事後分布の特徴を推定するためにサンプル統計量をMCMC出力から計算することができます。
StateBase パッケージ[53]は、多くの事後分布推定の計算に利用されています。
いくつかの利用可能な事後分布要約統計量を、以下のコードブロックに示します。
## 統計量要約
>>> describe(sim1)
Iterations = 252:10000
Thinning interval = 2
Chains = 1,2,3
Samples per chain = 4875
Empirical Posterior Estimates:
Mean SD Naive SE MCSE ESS
beta[1] 0.5971183 1.14894446 0.0095006014 0.016925598 4607.9743
beta[2] 0.8017036 0.34632566 0.0028637608 0.004793345 4875.0000
s2 1.2203777 2.00876760 0.0166104638 0.101798287 389.3843
Quantiles:
2.5% 25.0% 50.0% 75.0% 97.5%
beta[1] -1.74343373 0.026573102 0.59122696 1.1878720 2.8308472
beta[2] 0.12168742 0.628297573 0.80357822 0.9719441 1.5051573
s2 0.17091385 0.383671702 0.65371989 1.2206381 6.0313970
## 最高事後密度区間 (HPD: Highest Posterior Density Intervals)
>>> hpd(sim1)
95% Lower 95% Upper
beta[1] -1.75436235 2.8109571
beta[2] 0.09721501 1.4733163
s2 0.08338409 3.8706865
## 相互相関 (Cross-Correlations)
>>> cor(sim1)
beta[1] beta[2] s2
beta[1] 1.000000000 -0.905245029 0.027467317
beta[2] -0.905245029 1.000000000 -0.024489462
s2 0.027467317 -0.024489462 1.000000000
## 自己相関 (Lag-Autocorrelations)
>>> autocor(sim1)
Lag 2 Lag 10 Lag 20 Lag 100
beta[1] 0.24521566 -0.021411797 -0.0077424153 -0.044989417
beta[2] 0.20402485 -0.019107846 0.0033980453 -0.053869216
s2 0.85931351 0.568056917 0.3248136852 0.024157524
Lag 2 Lag 10 Lag 20 Lag 100
beta[1] 0.28180489 -0.031007672 0.03930888 0.0394895028
beta[2] 0.25905976 -0.017946010 0.03613043 0.0227758214
s2 0.92905843 0.761339226 0.58455868 0.0050215824
Lag 2 Lag 10 Lag 20 Lag 100
beta[1] 0.38634357 -0.0029361782 -0.032310111 0.0028806786
beta[2] 0.32822879 -0.0056670786 -0.020100663 -0.0062622517
s2 0.68812720 0.2420402859 0.080495078 -0.0290205896
## itelation ごとの状態空間変化率 (State Space Change Rate)
>>> changerate(sim1)
Change Rate
beta[1] 0.844
beta[2] 0.844
s2 1.000
Multivariate 1.000
## DIC情報量 (Deviance Information Criterion)
>>> dic(sim1)
DIC Effective Parameters
pD 13.828540 1.1661193
pV 22.624104 5.5639015
出力サブセット化
さらに、サンプラの出力をサブセット化して、選択された itelation 、パラメータ、および chain で事後推論を実行することができます。
## サブセット化されたサンプラ出力
>>> sim = sim1[1000:5000, ["beta[1]", "beta[2]"], :]
>>> describe(sim)
Iterations = 1000:5000
Thinning interval = 2
Chains = 1,2,3
Samples per chain = 2001
Empirical Posterior Estimates:
Mean SD Naive SE MCSE ESS
beta[1] 0.62445845 1.0285709 0.013275474 0.023818436 1864.8416
beta[2] 0.79392648 0.3096614 0.003996712 0.006516677 2001.0000
Quantiles:
2.5% 25.0% 50.0% 75.0% 97.5%
beta[1] -1.53050898 0.076745702 0.61120944 1.2174641 2.6906753
beta[2] 0.18846617 0.618849048 0.79323126 0.9619767 1.4502109
File I/O
将来の julia セッションで処理するためにサンプラの出力を外部ファイルに保存したい場合には、読み取りと書き込みの両方が提供されています。
## 外部ファイルへの書き込みと読み取り
write("sim1.jls", sim1)
sim1 = read("sim1.jls", ModelChains)
サンプラの再スタート
収束診断または事後分布要約の結果から、推論のために事後分布から追加の描画が必要であると示唆されることがあります。
そのような場合は、以下に示すように、 mcmc() 関数を使用して、以前に生成された出力変数からサンプラを再スタートすることができます。
## サンプラの再スタート
>>> sim = mcmc(sim1, 5000)
>>> describe(sim)
Iterations = 252:15000
Thinning interval = 2
Chains = 1,2,3
Samples per chain = 7375
Empirical Posterior Estimates:
Mean SD Naive SE MCSE ESS
beta[1] 0.59655228 1.1225920 0.0075471034 0.014053505 6380.79199
beta[2] 0.80144540 0.3395731 0.0022829250 0.003954871 7372.28048
s2 1.18366563 1.8163096 0.0122109158 0.070481708 664.08995
Quantiles:
2.5% 25.0% 50.0% 75.0% 97.5%
beta[1] -1.70512374 0.031582137 0.58989089 1.1783924 2.8253668
beta[2] 0.12399073 0.630638800 0.80358526 0.9703569 1.4939817
s2 0.17075261 0.382963160 0.65372440 1.2210168 5.7449800
プロッティング
Mamba でのサンプラ出力のプロットは、Gadfly パッケージ[51]によって成り立っています。
要約プロットは、plot および draw 機能を使用して作成および、ファイルへの書き込むができます。
## 標準の要約プロット（トレースプロットと、密度プロット）
p = plot(sim1)
## プロットを svg ファイルへ保存
draw(p, filename="summaryplot.svg")
トレースプロットと、密度プロット
plot 関数は、自己相関プロットおよび実行時平均プロットを作成するためにも使用できます。
凡例をつけるためにオプションの legend 引数を指定することができます。
プロットの配列を作成して、 draw 関数へ渡すことができます。
nrow と ncol オプションを使用して、各描画に含まれるプロットの行数と列数を決定します。
## 自己相関プロットと、実行時平均プロット
p = plot(sim1, [:autocor, :mean], legend=true)
draw(p, nrow=3, ncol=2, filename="autocormeanplot.svg")
自己相関プロットと、実行時平均プロット
## ペアワイズ等高線プロット
p = plot(sim1, :contour)
draw(p, nrow=2, ncol=2, filename="contourplot.svg")
ペアワイズ事後分布密度等高線プロット
コンピュータ上のパフォーマンス
今回の回帰例に適用した異なるサンプリングアルゴリズムについて、計算実行時間を記録しました。
実行環境はインテルi5-2500 CPU @ 3.30GHzのデスクトップコンピュータで実行されました。
結果を以下の表に要約します。
これは、パッケージそのままのコンピューティングパフォーマンスを測定することのみを目的としており、サンプリングアルゴリズムによって生成される出力のさまざまな効率を考慮していないことに注意してください。
Mambaで選択できるサンプリングアルゴリズムの1秒あたりの結果描画回数
| Adaptive Metropolis | Gibbs | NUTS | Slice | ||
|---|---|---|---|---|---|
| Within Gibbs | Multivariate | Gibbs | NUTS | Within Gibbs | Multivariate |
| 16,700 | 11,100 | 27,300 | 2,600 | 13,600 | 17,600 |
モデル開発とテスト
モデルの開発とテストをサポートするために、すべてのパッケージ関数にコマンドラインアクセスが用意されています。
使用可能な関数の例は、下のコードブロックに示されています。
これらおよびその他の関連機能のドキュメントは、MCMCタイプセクションにあります。
## モデル開発とテスト
setinputs!(model, line) # インプットノードの値を設定
setinits!(model, inits[1]) # 初期値を設定
setsamplers!(model, scheme1) # サンプリングスキーマを設定
showall(model) # ノード情報の詳細を表示
logpdf(model, 1) # サンプリングブロック1 の対数確率密度合計
logpdf(model, 2) # サンプリングブロック2 の対数確率密度合計
logpdf(model) # 全てのサンプリングブロックの対数確率密度合計
sample!(model, 1) # サンプリングブロック1 の値をサンプリング
sample!(model, 2) # サンプリングブロック2 の値をサンプリング
sample!(model) # 全てのサンプリングブロックの値をサンプリング
この例では、関数 setinputs!, setinits!, および setsampler! によって、インプットノードの値、初期値、およびサンプリング・スキームを model オブジェクトから手動で設定しています。また、これらは logpdf および sample! の実行前に呼び出す必要があります。
更新された model オブジェクトは呼び出されたときに返されます。 返されない場合は、指定された値に問題がある可能性があります。
メソッド showall は、すべての model ノードの値、および属性の詳細な要約を出力します。 logpdf は、指定されたサンプリングブロック（第2引数）に関連付けられたノード上の対数確率密度を合計します。 sample! はノードの値についてMCMCサンプルを生成します。
数値以外の結果が帰ってきた場合、logpdf 実行時では分布形式の定義 (distributional specification) 上の問題を示し、sample! 実行時ではサンプリング関数で問題がある可能性が予想されます。
block 引数はオプションです。 指定しないままにすると、対応する関数がすべてのサンプリングブロックに適用されます。
この仕様により、サンプラの一部または全部のテストが可能になります。
// 随時更新