【競プロ】期待値DPの雰囲気を掴んだ気になった話(お寿司食べたい) #AtCoder

こんにちは、dirardです。
最近はAtCoderで競プロをしたり(してなかったり)してします。
解いていて初めはわからなかった問題の備忘録として本記事を書きます。
競プロerの方々は仲良くしてくださるとうれしいです。

事の発端

それはAtCoderにてEDPC(Educational DP Contest / DP まとめコンテスト)を埋めていた時のことであった。

順調に進んでいたかに思えたその瞬間ある問題に出会った。

その問題が以下の問題である。

J - Sushi

問題文

$N$ 枚の皿があります。
皿には $1, 2, \ldots, N$ と番号が振られています。
最初、各 $i$ ($1 \leq i \leq N$) について、皿 $i$ には $a_i$ ($1 \leq a_i \leq 3$) 個の寿司が置かれています。
すべての寿司が無くなるまで、太郎君は次の操作を繰り返し行います。

$1, 2, \ldots, N$ の目が等確率で出るサイコロを振り、出目を $i$ とする。皿 $i$ に寿司がある場合、皿 $i$ の寿司を $1$ 個食べる。皿 $i$ に寿司が無い場合、何も行わない。

すべての寿司が無くなるまでの操作回数の期待値を求めてください。

制約

入力はすべて整数である。

$1 \leq N \leq 300$

$1 \leq a_i \leq 3$

問題リンク

ぐぬぬ…なんじゃこりゃ…さっぱりわからない…わからなさすぎてわからない…。

ということで、今回の目標はこのSushiを無事に完食することです。

Sushiの前に…

※DPはDynamic Programmingの略です。
※DPについて知りたい方は別の記事を参考にしてください。

Sushiはいろいろと複雑なので期待値DPの問題として類題を見てみることにします。

以下の問題(ABC 280 E.Critical Hit)を考えます。

問題概要

体力が $N$であるモンスターが $1$ 体います。高橋君はモンスターに対し、モンスターの体力が $1$ 以上残っている限り繰り返し攻撃を行います。
高橋君は $1$ 回の攻撃で、$\dfrac{P}{100}$の確率でモンスターの体力を $2$ 減らし、 $1−\dfrac{P}{100}$の確率でモンスターの体力を $1$ 減らします。
モンスターの体力が $0$ 以下になるまでに行う攻撃回数の期待値を $mod$ $ 998244353$ で出力してください。

問題リンク

Sushiよりはわかりやすいような気もするけど解説を読んでもよくわからない…。
ということで、問題を確率を排除した形式に一度替えてみようと思います。

Critical Hit改題

体力が$N$であるモンスターが$1$体います。
高橋君はモンスターに対し、モンスターの体力が$1$以上残っている限り繰り返し攻撃を行います。
高橋君は$1$回の攻撃でモンスターの体力を$1$減らします。
モンスターの体力が $0$ 以下になるまでに行う攻撃回数の期待値を $mod$ $ 998244353$ で出力してください。

今回の改題では確率的な行動はなく、確定で体力を$1$減らすとしています。
そのため、答えは$N$ $mod$ $998244353$ であるのは明らかですが、

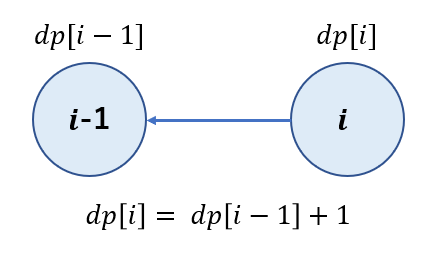
$$dp[i] := モンスターの体力がNである時の必要な攻撃回数(の期待値)$$

として状態遷移を考えてみます。

上記の図はモンスターの体力が $i$ である時に攻撃により残りの体力が $i-1$ に遷移することを表しています。
体力が $i$ である状態での必要攻撃回数 $dp[i]$ は体力が $i-1$ である状態での必要攻撃回数 $dp[i-1]$ に $i$ から $i-1$ にする際の $1$ 回を加えればよいので、
$$dp[i] = dp[i-1] + 1$$
となっています。
$dp[0] = 0$ であるので、上記の式より残り体力 $N$ の時の必要攻撃回数は $N$ 回であるとわかります。(i=1~Nまで繰り返せばOK)

さて、ここで、
$$dp[i] := モンスターの体力がNである時の必要な攻撃回数$$
に無理やり確率の概念を持ち込んでみます。
今回は残り体力が $i$ の状態から $i-1$ の状態へ必ず(確率1で)遷移する。
これは、$dp[i]$ は $(dp[i-1] + 1)\times 1$ すなわち $(dp[i-1] + 1)\times (i
から i-1 へ遷移する確率)$ によって求められていると考えることができます。
これは大学受験でよく出る確率漸化式と同様の考え方です。
実際に期待値DPもこの考え方で解くことができます！

Critical Hitを解いてみる！

ではCritical Hitに戻ってみようと思います。

先ほどと同様に
$$dp[i] := モンスターの体力がNである時の必要な攻撃回数の期待値$$
として状態遷移を考えます。

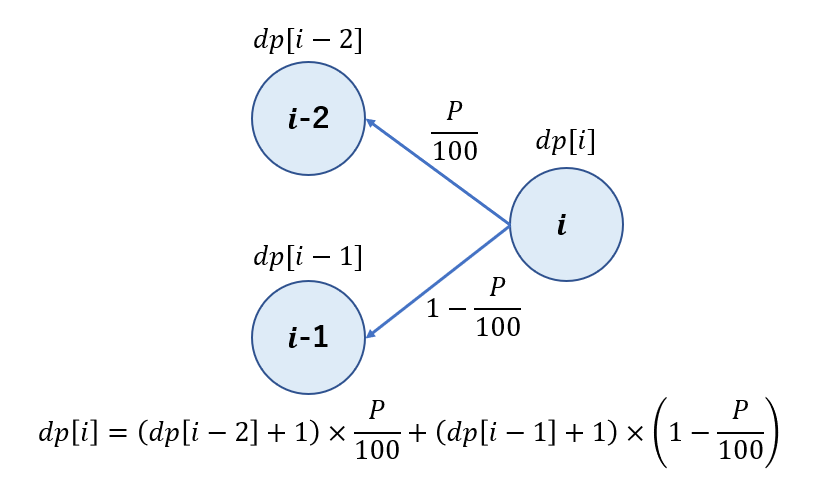
改題での最後の考察と同様にすると遷移が得られます。
具体的には、 $dp[i]$ は $(dp[iから遷移可能な状態] + 1)\times (その状態へ遷移する確率)$の和で得られます。
すなわち、
$$dp[i] = (dp[i-2] + 1)\times \frac{P}{100} + (dp[i-1] + 1)\times(1-\frac{P}{100})$$
となります。
この式を整理すると、
$$dp[i] = 1 + dp[i-2]\times \frac{P}{100} + dp[i-1]\times(1-\frac{P}{100})$$
となります。
上記の式をi=1~N まで繰り返し、 $dp[0]=0$ であることと、$2$ ダメージを与えて$-1$ になるときに注意すると解が求まります。

※$-1$ を回避するには $i-2$ への遷移を $\max(i-2, 0)$ への遷移として回避してもよい。

いよいよSushiをいただく

Critical Hitでの考え方をもとにSushiを食べたいと思います。

問題文再掲

J - Sushi

問題文

$N$ 枚の皿があります。
皿には $1, 2, \ldots, N$ と番号が振られています。
最初、各 $i$ ($1 \leq i \leq N$) について、皿 $i$ には $a_i$ ($1 \leq a_i \leq 3$) 個の寿司が置かれています。
すべての寿司が無くなるまで、太郎君は次の操作を繰り返し行います。

$1, 2, \ldots, N$ の目が等確率で出るサイコロを振り、出目を $i$ とする。皿 $i$ に寿司がある場合、皿 $i$ の寿司を $1$ 個食べる。皿 $i$ に寿司が無い場合、何も行わない。

すべての寿司が無くなるまでの操作回数の期待値を求めてください。

制約

入力はすべて整数である。

$1 \leq N \leq 300$

$1 \leq a_i \leq 3$

問題リンク

各皿の残り数をインデックスに配列を管理すると $dp[4][4][4]...[4]$ と$4^{300}$ の長さを管理しなければならないのでダメ…工夫が必要です。

例えば2皿で、「1皿目に残り1貫、2皿目に残り2貫である状態」と「1皿目に残り2貫、2皿目に残り1貫である状態」は同じと考えられるので、残り1, 2, 3貫の皿がそれぞれ何皿あるかを考えればよいといえそうです。

$$dp[i][j][k] = (残り1貫の皿がi, 皿残り2貫の皿がj皿, 残り3貫の皿がk皿の状態から必要な操作回数の期待値)$$

とするとよさそうです。

状態遷移は以下のようになります。

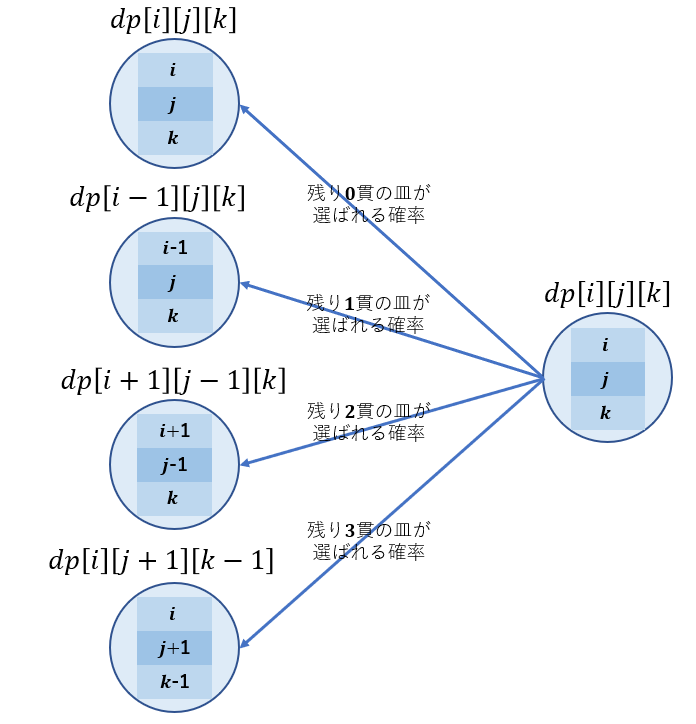
状態 $(i, j, k)$ の時に皿は、残り0, 1, 2, 3貫の皿を選ぶ可能性があるので、それぞれを選んだ時が対応しています。
例えば、残り2貫の皿を選んだ場合、残り2貫の皿が減り、その結果残り1貫の皿が増えるので $(i, j, k) \rightarrow(i+1, j-1, k)$ となります。

また、状態 $(i, j, k)$ のときに

残り0貫の皿を選ぶ確率 = $1 - \dfrac{i + j + k}{N}$
残り1貫の皿を選ぶ確率 = $\dfrac{i}{N}$
残り2貫の皿を選ぶ確率 = $\dfrac{j}{N}$
残り3貫の皿を選ぶ確率 = $\dfrac{k}{N}$

です。

ここで、Critical Hitでの考察を思い出すと

$dp[ある状態]$ は $(dp[ある状態から遷移可能な状態] + 1)\times (その状態へ遷移する確率)$の和で得られる

ということであったので、

\begin{align}
dp[i][j][k] &= &(dp[i][j][k] + 1)\times(1 - \dfrac{i + j + k}{N}) \\
&&+ (dp[i-1][j][k] + 1)\times \dfrac{i}{N} \\
&&+ (dp[i+1][j-1][k] + 1)\times \dfrac{j}{N} \\
&&+ (dp[i][j+1][k-1] + 1)\times \dfrac{k}{N} \\
&& \\
&=& 1 + dp[i][j][k]\times(1 - \dfrac{i + j + k}{N}) \\
&&+ (dp[i-1][j][k] + 1)\times \dfrac{i}{N} \\
&&+ (dp[i+1][j-1][k] + 1)\times \dfrac{j}{N} \\
&&+ (dp[i][j+1][k-1] + 1)\times \dfrac{k}{N}
\end{align}

となります。

$dp[i][j][k]$ が右辺にもあるので移項して整理すると

\begin{align}
dp[i][j][k] &= &\dfrac{N}{i+j+k}\\
&&+ (dp[i-1][j][k] + 1)\times \dfrac{i}{i+j+k} \\
&&+ (dp[i+1][j-1][k] + 1)\times \dfrac{j}{i+j+k} \\
&&+ (dp[i][j+1][k-1] + 1)\times \dfrac{k}{i+j+k}
\end{align}

となります。

上記の式から解を $O(N^3)$ で求めることができます。
めでたしめでたし！！！

$dp[i][j][k]$ を求める際に、$dp[i][j+1][k-1]$、 $dp[i+1][j-1][k]$ が必要になるため、3重loopの順番は

rep(k) rep(j) rep(i)

とする必要がある(はず)。

無事に寿司を完食した(ACした)コード

きれいではないので載せる価値もないですが…。(C++です)

#include <bits/stdc++.h>
using namespace std;

int N;
int a[309];
double dp[309][309][309];
int cnt[4];

int main(){
    cin >> N;
    for(int i=1;i<=N;i++){
        cin >> a[i];
        cnt[a[i]]++;
    }

    for(int k=0;k<=N;k++){
        for(int j=0;j<=N;j++){
            for(int i=0;i<=N;i++){
                if(i+j+k==0) continue;
                double exp = 1.0 * N / (i+j+k);
                if(i>0) exp += dp[i-1][j][k] * i / (i+j+k);
                if(j>0) exp += dp[i+1][j-1][k] * j / (i+j+k);
                if(k>0) exp += dp[i][j+1][k-1] * k / (i+j+k);
                dp[i][j][k] = exp;
            }
        }
    }

    cout << fixed << setprecision(15) << dp[cnt[1]][cnt[2]][cnt[3]] << endl;
    return 0;
}

まとめ

期待値DPは基本的には大学受験御用達の確率漸化式の考え方
(期待値の期待値みたいな考え方)
状態遷移はゴールから遠い(indexが大きい)ものからゴールに近い(indexが小さい)ものへと向かって移る
loopの変数の順番に気を配る必要がある(かもしれない)
メモ化再帰での実装なら添え字の順番は特に気にしなくてよいらしい
高橋君は勇者
寿司ネタはマグロが好き！

※Qiita上で数式を複数行書く際にflalignのようなことができるかご存じの方は教えてくださるとうれしいです…。

【競プロ】期待値DPの雰囲気を掴んだ気になった話(お寿司食べたい)

事の発端

J - Sushi

問題文

制約

Sushiの前に…

問題概要

Critical Hit改題

Critical Hitを解いてみる！

いよいよSushiをいただく

問題文再掲

J - Sushi

問題文

制約

コメント

無事に寿司を完食した(ACした)コード

まとめ