2020年の論文で少し古いですがやっていることが面白いと感じたのでメモ。
概要
モデルの効率的な推論手法にearly exitがあるが、これをBERTに適用した話。(だと思っています)
ポイントはトランスフォーマーブロックって何段も積み重ねているけど、途中までで十分じゃないの?ということ。
Architecture
一番左のBackboneというのが通常のBERTです。
モデルはBERTの各Transformerブロックに Student Classifier(0~L-2)を付け加えた構成になっています。
図はバッチ推論(バッチサイズ4)の例です。
まず、Transformer 0までを計算し、Student Classifier 0を計算します。
その結果が十分に自信が持てるもの(図のサングラス)であった場合はそれを最終出力としてそれ以降の計算はスキップします。
それ以降は確信が持てなかったものに対して続きのlayerの計算を行って…ということを繰り返します。
最後までStudent Classifierの結果で自信が持てなかった場合は通常通りTeacher Classifierの出力が採用されます。
という流れで自信が持てた段階で以降の計算を行わずスキップするという策をとります。
学習方法
以下の流れで行います。
- BackBone部分のFine-Tuningを行う(Branchは考えない)
- Backboneのパラメータを固定してBranchの学習を行う
Branchの学習はTeacher Classifierを親とするSelf-distilling(自己蒸留)で行います。
具体的には $i$ 番目のStudentに対し、
Teacher Classifierの出力を $p_t = Teacher Classifier(h_{L-1})$、
Student Classifierの出力を $p_s = Student Classifier_i(h_{i})$ とすると、
D_{KL}(p_s, p_t) = \sum_{i=1}^N p_s(i) \log \frac{p_s(i)}{p_t(i)}
をTeacherとStudentの誤差(分布の差)として考えることができます。
損失関数は全Studentについて$D_{KL}(p_s, p_t)$の和を考えて、
Loss(p_{s_0}, ..., p_{s_{L-2}}, p_t) = \sum_{i=0}^{L-2} D_{KL}(p_{s_i}, p_t)
とします。
これにより各Student ClassifierがTeacher Classifierに近づくように学習されます。
推論時に自信があるかどうかの判断方法
推論時にStudent Classifierの出力結果が自信を持てるものかどうかの判断は以下のUncertaintyをベースに行う。
Uncertainty = \frac{\sum_{i=1}^N p_s(i) \log p_s(i)}{\log \frac{1}{N}}
ここでの$N$はラベルのクラス数をあらわす。
Uncertaintyはクラスの予測結果がクラスによって差が大きい場合に小さく、差が小さい場合に大きくなる。
Uncertainty計算例:

Uncertainty = 0.28812071961329816
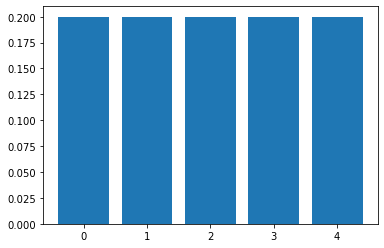
Uncertainty = 1.0000000000000002
このUncertaintyの値に対して閾値を設け、それ以下ならそれ以降をスキップする。
