今更ながらの誤差逆伝播法(BackPropagation)[必殺技ではない…]

所属先で「ゼロから作るDeepLearning」(ゼロつく)の勉強会があり、5章 誤差逆伝播法(BackPropagation)を担当したので備忘録として投稿。

Amazonリンク

今回の(勝手な)問題設定

※Deep Learningの会ですが、今回はDeep Learningはやりません。

観測されたデータを $x$ とし $y$ を正解の値(ラベル)、 $\epsilon$ を誤差、 $a$ と $b$ を学習するパラメータとして、線形回帰 $y = ax + b + \epsilon$ でフィッティングする問題を考える。

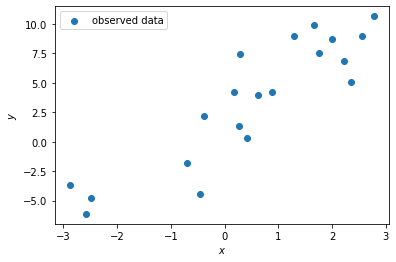
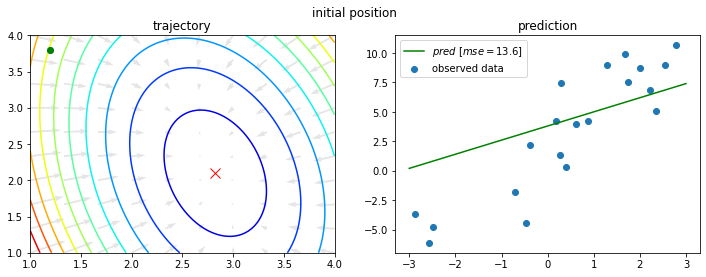
また、データ $x_i$ は20件観測されており、各 $x_i$ に対し正解 $y_i$ も与えられているとする。(下図)

これらの観測データから誤差 $\epsilon_i = y_i - (ax_i + b)$ が求められる。

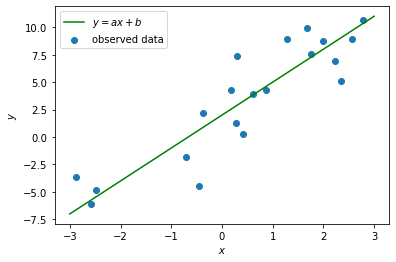
上記のデータに対して下図のように良きパラメータ $a$ 、$b$ を求めたい！

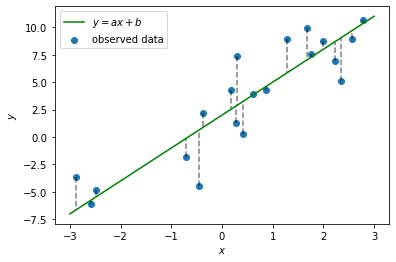
よくやる手法として、直線と各観測値との誤差 $\epsilon_i = y_i - (ax_i + b)$ (下図の点線部分)の二乗和 $S = \sum_{i=1}^{20} \epsilon_i^2 = \sum_{i=1}^{20} (y_i - (ax_i + b))^2$ を考え、それが最小となるパラメータを求めるやり方がある。(最小二乗法)

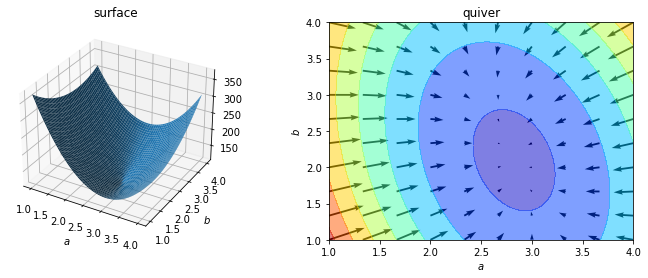
二乗和誤差 $S = \sum_{i=1}^{20} (y_i - (ax_i + b))^2$ は $a$、$b$ の関数となっている。

二乗和誤差の概形と勾配(最急降下方向)は下図。

ニューラルネットワークの学習の流れ(今回はニューラルネットワークじゃないけど…)

1. ミニバッチの用意 (全データ20件)
2. 順伝播 ( $ax_i + b$ の計算)
3. 損失関数 (二乗和誤差) の計算
4. 勾配 ( $\frac{\partial S}{\partial a}$ と $\frac{\partial S}{\partial b}$ ) の計算 <- 今回はここの効率化がメインターゲット
5. 勾配法によるパラメータの更新
6. 1.に戻って繰り返す

※ ( ) 内は今回の問題設定における対応箇所 (今回の問題は解析に解けるという点は目を瞑る)

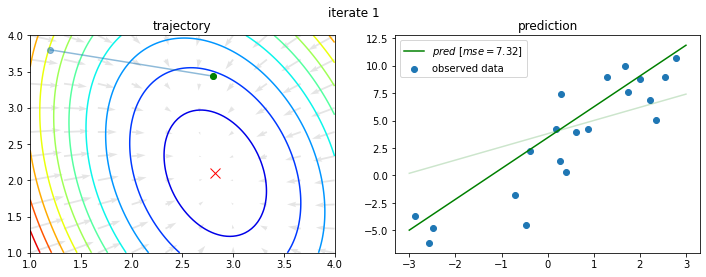
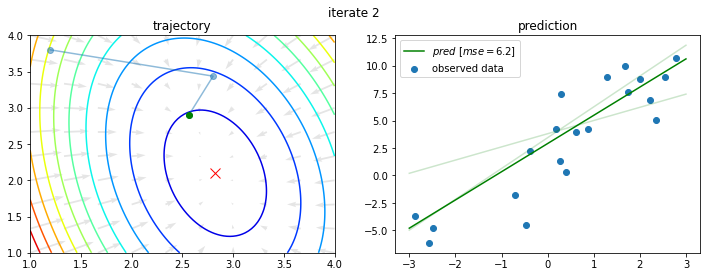
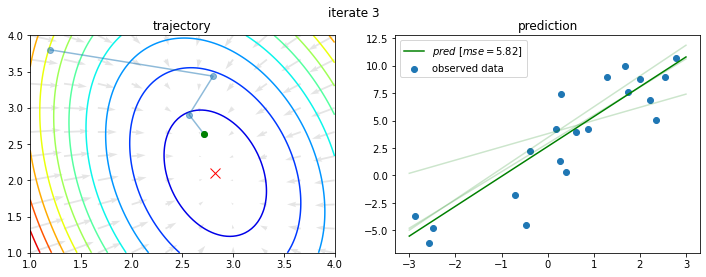
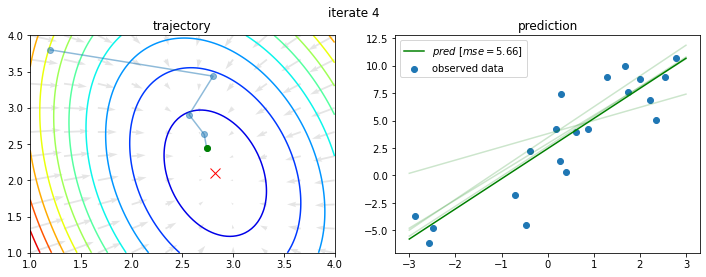
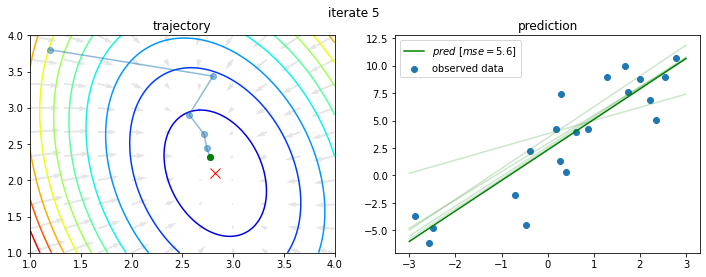
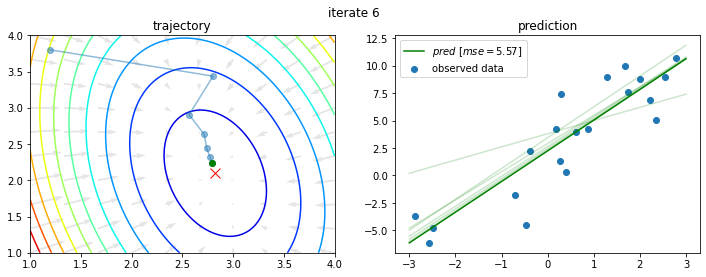
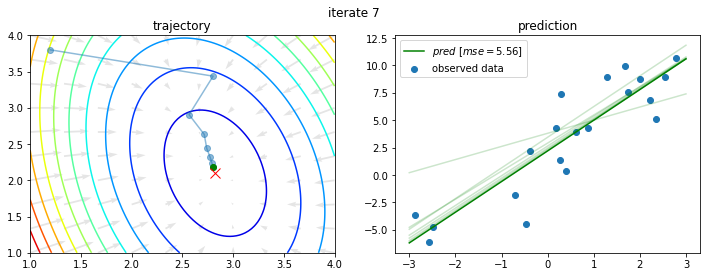
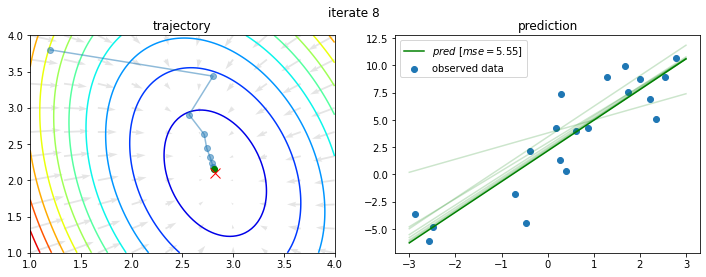
今回の問題に対し、初期値を $a_0 = 1.2$、$b_0 = 3.8$ として上記を10回繰り返すと以下のようになる。

このように学習がなされるわけであるが、4章では数値微分で勾配が求められることを学んだ(はず)。

しかし、数値微分はパラメータ数が増えると計算量が膨大になる(理由はあとで)。

そこで、勾配の計算を効率よく行いパラメータを更新する方法として誤差逆伝播法がある。

<余談>

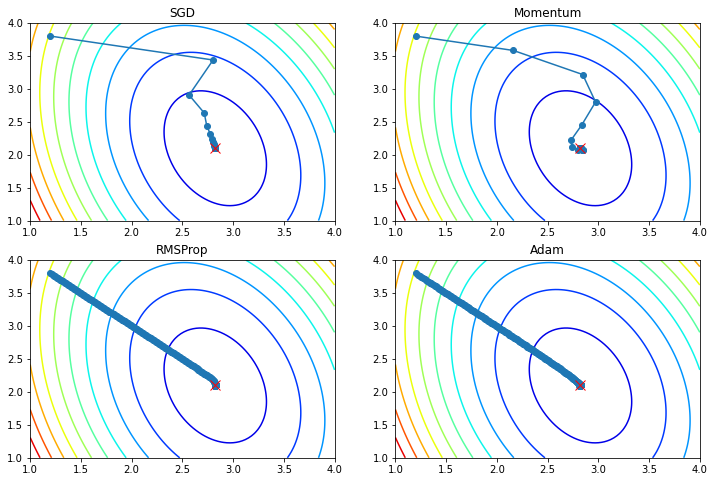
先ほどのパラメータ更新は (確率的)勾配降下法(SGD) で行ったが、パラメータの更新方法(最適化手法)は他のもある。
6章で触れられているので興味があれば、、、。

数値微分(4章の登場人物)

• 4章では差分を使う方法(中心差分・前方差分etc...)を学んだ(はず) 。
• 前方差分による数値微分：$\frac{\partial E}{\partial w_i} \approx \frac{E(..., w_i + \epsilon, ...) - E(..., w_i, ...)}{\epsilon}$
• 今回の誤差逆伝播法では自動微分を使う。 (自動微分の詳細は後ほど)

連鎖律(chain rule)

合成関数の微分の話。自動微分、誤差逆伝播法の前段の知識として必要である。
合成関数のパターンは無限に考えられるが、ここでは2つの型を取り上げてみる。

1変数関数version

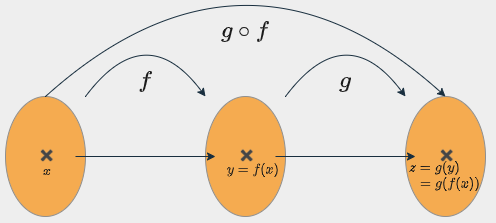
以下の関数を考える。

$y = f(x)$、$z = g(y)$

($z = g(f(x))$)

上記の $z$ は $x$ の関数であるが、$z$ の $x$ による微分は

$\frac{d z}{d x} = \frac{d z}{d y}\frac{d y}{d x}$

となる。(1変数関数の微分における連鎖律、証明略)

形式的には段階的に微分したものを掛け合わせることで最終的な微分が求められる。

<計算例>

$y = 2x + 1$、$z = y^2$を考える。

($z = y^2 = (2x + 1)^2$)

このとき、

$\frac{dz}{dy} = \frac{d}{dy}(y^2) = 2y$

$\frac{dy}{dx} = \frac{d}{dy}(2x + 1) = 2$

なので、

$\frac{d z}{d x} = \frac{d z}{d y}\frac{d y}{d x} = 2y\cdot 2 = 4y = 4(2x + 1) = 8x + 2$

ちなみに、この程度であれば直接計算もできる。

$\frac{dz}{dx} = \frac{d}{dx}(2x + 1)^2 = \frac{d}{dx}(4x^2 + 4x + 1) = 8x + 2$

2変数関数version

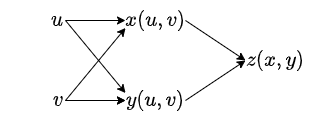
以下の関数を考える。

$x = x(u, v)$、$y = y(u, v)$、$z = z(x(u, v), y(u, v))$

このとき、

$\frac{\partial z}{\partial u} = \frac{\partial z}{\partial x}\frac{\partial x}{\partial u} + \frac{\partial z}{\partial y}\frac{\partial y}{\partial u}$

$\frac{\partial z}{\partial v} = \frac{\partial z}{\partial x}\frac{\partial x}{\partial v} + \frac{\partial z}{\partial y}\frac{\partial y}{\partial v}$

となる。(2変数関数の偏微分における連鎖律、証明略)

$\frac{\partial z}{\partial u}$ を求めるには、以下のように $z$ から $u$ までたどり、各経路の結果を足し合わせれば良いとわかる。

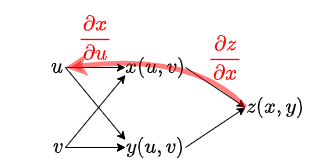
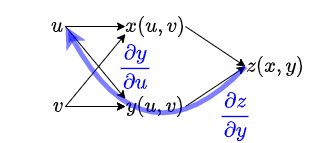
このように順にたどることによって、一見難しい関数でも微分を計算することが可能になる。

他の型の合成関数に対してもここで見たように流れを図示して順にたどることで連鎖律を可視化することが可能である。

ここで見た経路を表現する方法として計算グラフと呼ばれるものがある。誤差逆伝播法では簡単な関数をつなぎ合わせた計算グラフを上記のような経路をたどる方法で勾配を計算していると考えることができる。

(計算グラフを持ち出さず「数式(連鎖律)+出力層側から勾配を計算する」のみでも理解可能、というのも計算グラフはその過程を可視化しているだけという考えもできるため)

計算グラフには視覚的にわかりやすい、局所的な計算を扱える等のメリットがある。(数式でも局所的な議論は可能だが、、、)

途中経過を視覚的に保存しておける点は良いと感じる。

計算グラフ

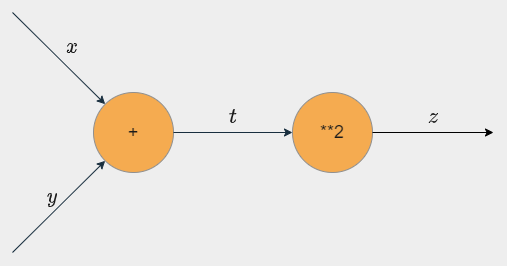
以下の図のように入力と出力を矢印で表し、演算(関数)をノード(丸いやつ)で表す。ここでは黒い矢印を順伝播、赤い矢印を逆伝播として扱う。

以下の計算グラフは
$t = x + y$、$z = t^2$
$(z = (x + y)^2)$
のものである。

逆伝播時には最終出力側から順伝播時の出力を入力で微分した値を逆伝播時の入力にかけて出力していく。これを入力層(勾配が必要な部分)まで繰り返し計算していく。

ここで、連鎖律を用いると、

$\frac{\partial z}{\partial x} = \frac{\partial z}{\partial t}\frac{\partial t}{\partial x}$

$\frac{\partial z}{\partial y} = \frac{\partial z}{\partial t}\frac{\partial t}{\partial y}$

であるが、これは入力 $x$、$y$ の逆伝播の赤矢印の下に書いてある式と一致している($\frac{\partial z}{\partial z} = 1$であるため)。

具体的な計算は
$\frac{\partial z}{\partial z} = 1$、
$\frac{\partial z}{\partial t} = \frac{\partial}{\partial t}(t^2) = 2t = 2(x + y)$、
$\frac{\partial t}{\partial x} = \frac{\partial}{\partial t}(x + y) = 1$、
$\frac{\partial t}{\partial y} = \frac{\partial}{\partial t}(x + y) = 1$
より

$\frac{\partial z}{\partial z} = 1$
→ $\frac{\partial z}{\partial t} = \frac{\partial z}{\partial z}\frac{\partial z}{\partial t} = 1 \cdot 2t = 2t$
→ $\frac{\partial z}{\partial x} = \frac{\partial z}{\partial z}\frac{\partial z}{\partial t}\frac{\partial t}{\partial x} = \frac{\partial z}{\partial t}\frac{\partial t}{\partial x} = 2t \cdot 1 = 2t$、$\frac{\partial z}{\partial y} = \frac{\partial z}{\partial z}\frac{\partial z}{\partial t}\frac{\partial t}{\partial y} = \frac{\partial z}{\partial t}\frac{\partial t}{\partial y}　= 2t \cdot 1 = 2t$

という流れで前段の結果を使って行っていく。

このように計算グラフを使用して出力層側から勾配情報を入力層側へ伝達(逆伝播)していくことで勾配の計算が可能である。
このように出力層側から勾配情報を伝達しながら各パラメータについての勾配を求める手法を誤差逆伝播法という。

一般的に誤差逆伝播法という言葉はニューラルネットワークの学習方法として使われるので、今回の問題設定では誤差逆伝播法とは呼ばず、逆伝播による自動微分というべきかもしれない。

自動微分

• コンピューター上に実装された関数は基本的には四則演算や指数関数、対数関数等の初等関数に帰着される。
• それらの関数一つ一つの微分は別の初等関数によって表現できる。
• 入力層or出力層から順に計算グラフをたどる要領で勾配を伝達することで、自動的に微分を行うことができる。(bottom-up / top-down mode)
• 「入力層の次元 > 出力層の次元」ならtop-down mode、「入力層の次元 < 出力層の次元」ならbottom-up modeが良いとされる。
• 誤差逆伝播法はtop-down modeの自動微分といえる。(逆に誤差逆伝播法の一般の関数を対象に一般化したものがtop-down modeの自動微分という見方もできる)
• 数値微分は近似であるが、こちらは精度の高い値が求められる。

以下では、計算グラフを構築する各パーツ(紹介するものが全てではない)での逆伝播の出力についてみていく。

ほとんどの計算グラフはこれらのパーツの組み合わせとして表せる。

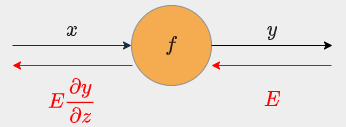
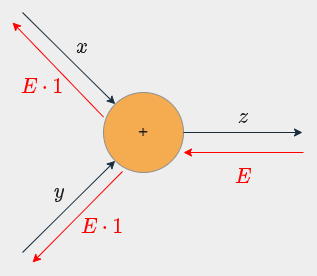
関数ノード

関数 $y = f(x)$ の場合、
逆伝播は入力値 $E$ に $f$ の微分 $\frac{\partial y}{\partial x}$ をかけた値が出力となる。

加算ノード

加算ノードの逆伝播は入力値 $E$ をそのまま出力する。

<詳細>
$z = x + y$ のとき、

• $\frac{\partial z}{\partial x} = \frac{\partial}{\partial x}(x + y) = 1$
• $\frac{\partial z}{\partial y} = \frac{\partial y}{\partial y}(x + y) = 1$

となるため。

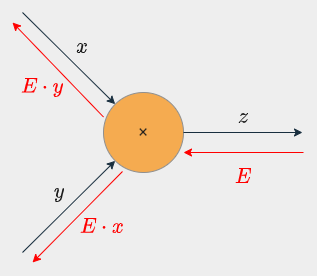
乗算ノード

乗算ノードの逆伝播は入力値 $E$ に順伝播を入れ替えた値をかけたものを出力する。

<詳細>
$z = xy$ のとき、

• $\frac{\partial z}{\partial x} = \frac{\partial}{\partial x}(xy) = y$
• $\frac{\partial z}{\partial y} = \frac{\partial y}{\partial y}(xy) = x$

となるため。

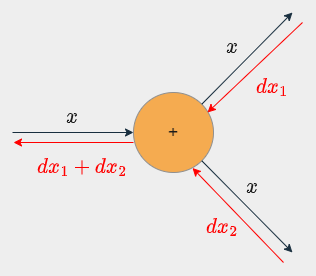
分岐ノード

分岐ノードの逆伝播は分岐先からの入力値(逆伝播値)の和を出力する。
※分岐が3個以上になっても同様に和を考えればよい。

計算グラフ例

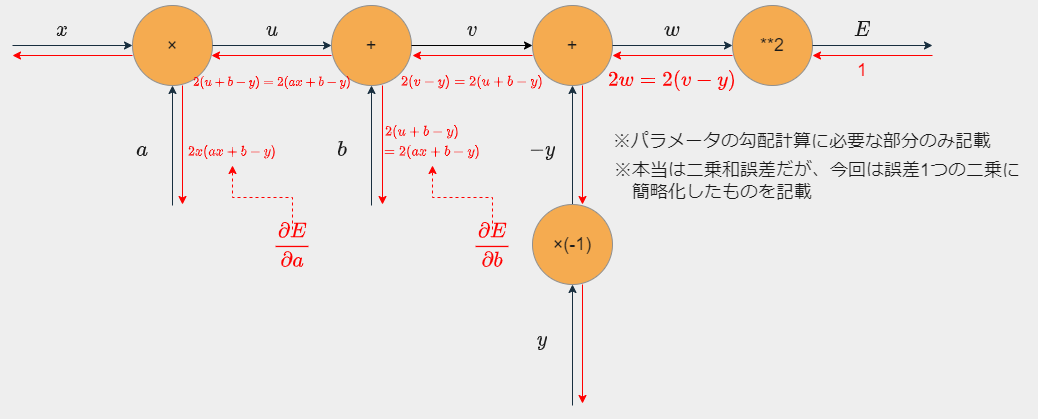
今回の問題設定での計算グラフは以下のようになる。
二乗和誤差は計算グラフが少し複雑になるので、簡略化版として1つのデータの二乗誤差 $\epsilon^2 = (y - (ax + b))^2 = (ax + b - y)^2$ についての計算グラフとしている。

• $u = ax$
• $v = u + b \ (= ax + b)$
• $w = v + (-y) \ (= ax + b -y)$
• $E = w^2 \ (= (ax + b -y)^2)$

※上図のように必要なところだけ求めればよいこともメリット

まとめ

誤差逆伝播法とは
top-down modeの自動微分(勾配を出力層側から伝達するやつ)を使用して勾配を計算し、勾配法で損失関数を最小化するようにパラメータを更新するニューラルネットワークの学習法
※誤差逆伝播法がなければ学習が不可能という話ではない(現実的な時間でできるとはいっていない)

<おまけ>誤差逆伝播法の推しポイント

数値微分との精度比較

• 数値微分(下の例は前方差分)であればパラメータごとに
  $\frac{\partial E}{\partial w_i} \approx \frac{E(..., w_i + \epsilon, ...) - E(..., w_i, ...)}{\epsilon}$
  を計算するが、これは近似値である。(近似精度も微妙)
• 一方で、誤差逆伝播法で求める勾配は計算グラフをたどることからもわかるように正確な勾配である。(機械的な問題で少し誤差はある)
• 以上より、誤差逆伝播法の方が精度が良い。また数値微分は、各勾配を計算する度に順伝播を行うため計算量が膨大になるという問題もある。

誤差逆伝播法を使わずに微分する方法との比較

• 誤差逆伝播法を使わない場合は、各パラメータについての勾配を求めるために毎回連鎖律を適応する。
• 誤差逆伝播法を使用する場合は連鎖律は1度のみ使用し、一度の逆伝播で全てのパラメータにおける勾配を求められる。
• 以上より計算回数を誤差逆伝播法により削減できる。