Medium
NumberOfDiscIntersections
Compute the number of intersections in a sequence of discs.
Task description
We draw N discs on a plane. The discs are numbered from 0 to N − 1. An array A of N non-negative integers, specifying the radiuses of the discs, is given. The J-th disc is drawn with its center at (J, 0) and radius A[J].
We say that the J-th disc and K-th disc intersect if J ≠ K and the J-th and K-th discs have at least one common point (assuming that the discs contain their borders).
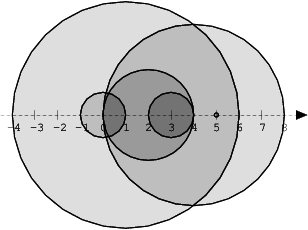
The figure below shows discs drawn for N = 6 and A as follows:
A[0] = 1
A[1] = 5
A[2] = 2
A[3] = 1
A[4] = 4
A[5] = 0
There are eleven (unordered) pairs of discs that intersect, namely:
discs 1 and 4 intersect, and both intersect with all the other discs;
disc 2 also intersects with discs 0 and 3.
Write a function:
class Solution { public int solution(int[] A); }
that, given an array A describing N discs as explained above, returns the number of (unordered) pairs of intersecting discs. The function should return −1 if the number of intersecting pairs exceeds 10,000,000.
Given array A shown above, the function should return 11, as explained above.
Write an efficient algorithm for the following assumptions:
- N is an integer within the range [0..100,000];
- each element of array A is an integer within the range [0..2,147,483,647].
Code walkthrough
class NumberOfDiscIntersectionsSolution {
/*
* N is an integer within the range [0..100,000];
* each element of array A is an integer within the range [0..2,147,483,647].
*/
public int solution(int[] A) {
int result = 0;
int[] dps = new int[A.length];
int[] dpe = new int[A.length];
for (int i = 0, t = A.length - 1; i < A.length; i++)
{
// The centers of discs are in the range [0, A.length - 1],
// so if two circles intersect, then they must intersect in the range [0, A.length - 1].
// So we can think that the start point of one disc is 0 even if this disc has negative part.
// E.g. If there is a input: A[0] = 1
// then this disc is start at 0-1=-1, end at 0+1=1 => [-1, 1]
// => [0, 1]
int s = i > A[i]? i - A[i]: 0;
// And also, we can drop all the parts in the right of A.length.
// E.g. If there is a input: A[4] = 4
// then this disc is start at 4-4=0, end at 4+4=8 => [0, 8]
// => [0, A.length - 1]
// i + A[i], if A[i] is max integer(2,147,483,647), then i+A[i] will be wrong (you will get a negative number)
// but don't worry about it, because the code "i + A[i]" be run only when "A[i] < t - i", and max t is A.length-1
// So we do not need a long type here.
int e = t - i > A[i] ? i + A[i]: t;
dps[s]++;
dpe[e]++;
}
int activeDiscs = 0;
for (int i = 0; i < A.length; i++)
{
// If there are new discs which are starting at i,
if (dps[i] > 0)
{
// then there new discs are all intersecting to active discs.
// dps[i] means there are dps[i] discs are starting
result += activeDiscs * dps[i];
// new started discs intersect to each other
// E.g. if dps[i] is 3, then the count of that they intersect to each other = 3+2+1 = 3*(3-1)/2
// Sum(1,2,...,n) = n*(n-1)/2
result += dps[i] * (dps[i] - 1) / 2;
// The function should return −1 if the number of intersecting pairs exceeds 10,000,000.
if (10000000 < result) return -1;
// of course that, these new started discs are also active discs
activeDiscs += dps[i];
}
// we added new started discs, then we should have a look at that
// if there are any disc is dying, of course, we should poll them out from active discs.
activeDiscs -= dpe[i];
}
return result;
}
}
Detected time complexity:
O(N)