画像リサイズのうんちく
- https://qiita.com/yoya/items/95c37e02762431b1abf0

こちらの記事からの派生です。

補間フィルタ

ビットマップ画像のリサイズ/縮小拡大は、各ピクセルの仕切り直しと考える事もできます。(主流は点光源の波の組み合わせですが、ここでは分かりやすいグリッドの方で説明します。

	src	resample	dst
拡大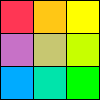
縮小

近傍の色を参考にこの白い隙間を埋める処理方式によって、リサイズ処理の結果が変わってきます。
色を埋める処理を補間フィルタ、その具体的なアルゴリズムを補間メソッドと呼びます。
レガシーな印象もありますが今でもよく使われる代表的な補間メソッドを紹介します。

補間カーネル

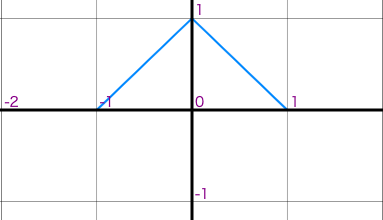
拡大でも縮小でも周囲のピクセルを適度な割合で混ぜて補間を行います。その混ぜ方は１次元の重み付け数列で表現できて、補間カーネルと呼びます。参考までに代表的なメソッドを並べます。

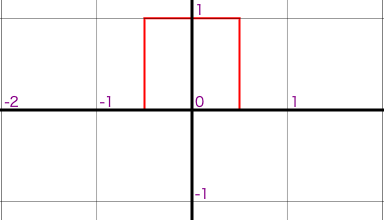
Nearest-Neighbor	Bi-Linear

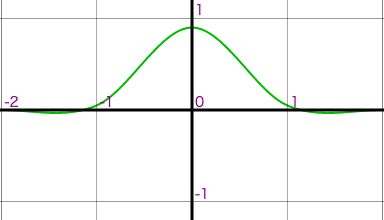
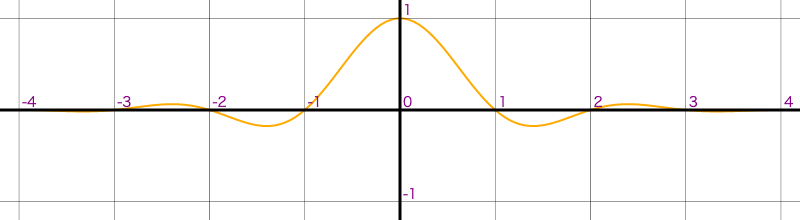
Bi-Cubic (b:1/3,c:1/3, mitchell)	Lanczos (lobe:4, lanczos4)

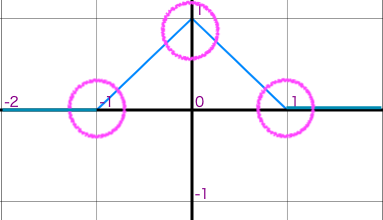
形状から、Nearest を Point フィルタ、Bi-Linear を Triangle フィルタ、Tent フィルタ、又は 2D だと Cone フィルタと呼ぶ事もあります。ちなみに、ImageMagick のフィルタ名は、この point, triangle を採用しています。
これら以外にも沢山の補間メソッドが提唱されています。

Nearest-Neighbor

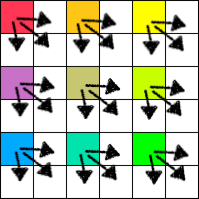
実用的な補間メソッドとして最も単純で最速です。隣からピクセルをコピーしてくるだけです。

src	resample	enlarge	interpolate	dst

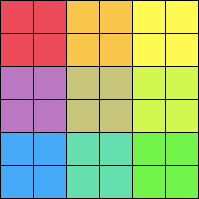実用的には、画像ビューア(ブラウザ含む)のウィンドウ枠をマウスで掴みグリグリ画像のサイズを変える時だけ Nearest-Neighbor で素早く表示し、マウスが止まってサイズが変わくなった時に改めて重たいけど画質が良い補間メソッドで表示し直す。といった使われ方をよくされます。

あと、色が変わらないといった稀有な特徴があり、GIF や PNG8 等のパレット画像のリサイズでは、この補間方式が使われる事も多いです。

分かりやすい欠点として、Nearest-Neighbor は拡大するにつれ、ピクセルが四角いまま膨らみドット絵のような表示になります。ジャギーといった表現をよくします。
逆に縮小する時はピクセルをところどころ読み飛ばすので、運次第で見た目と全然違う色、いわゆる偽色に変わったり、特定パターンによる模様が現れたりします。

Bi-Linear はそれらの問題をある程度解決します。

Bi-Linear

空白ピクセルの上下左右に１つしか色のピクセルが存在しない場合はそれをコピーしますが、左右又は上下にある場合はその二つの平均 (a+b)/2、上下左右４つある場合はその４つを平均 (a+b+c+d)/4 、といった具合に色を混ぜます。

src	resample	enlarge	interpolate	dst

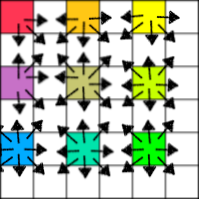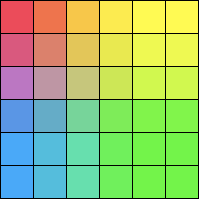Bi-Linear の欠点として、ジャギーが軽減される代わりに全体的にピンボケたように見えます。
また、テントの形をした補間フィルタは C1 連続でない為に、部分部分急激な色の変化をもたらし偽の輪郭が発生する事があります。

Bi-Cubic B,Cパラメータ

Bi-Linear に無かった C1 連続を導入して不自然さをある程度軽減します。隣の更に隣のピクセルまで参照します。


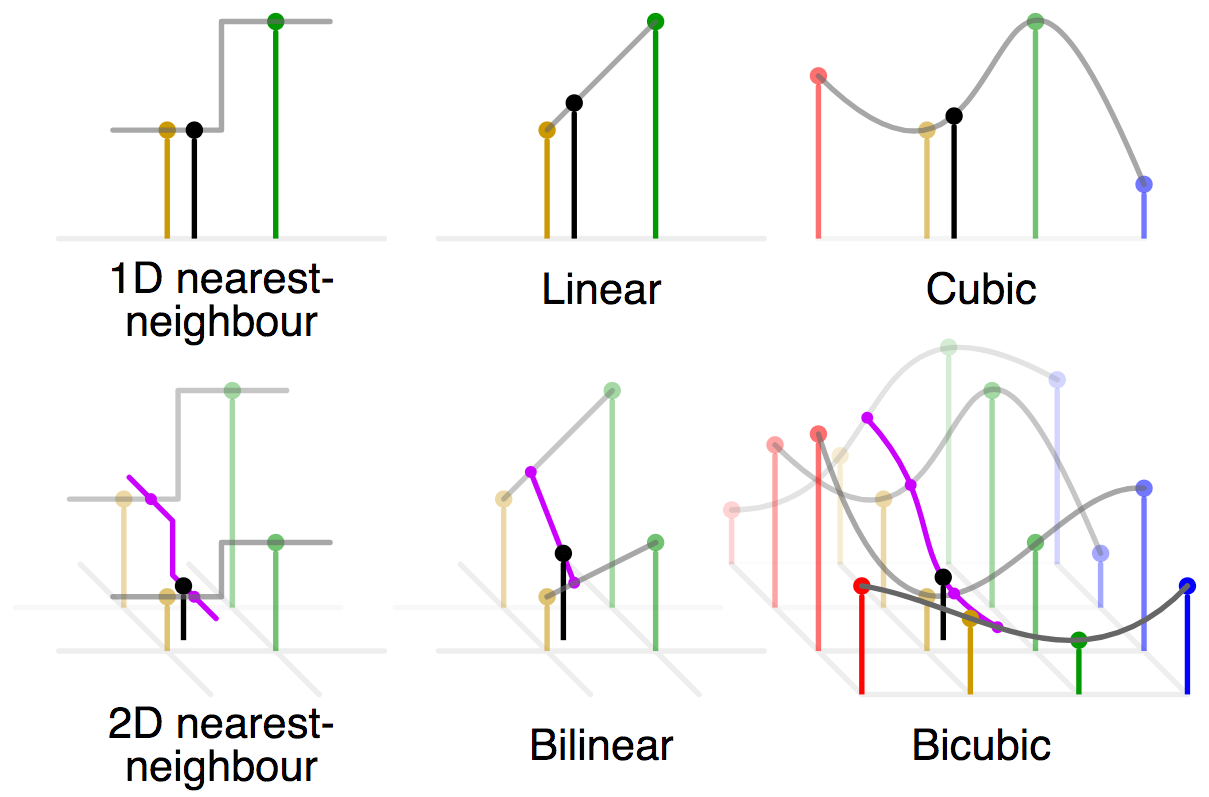転載元) https://en.wikipedia.org/wiki/Bicubic_interpolation

三次式の計算で処理はそこそこ重たいですが、"質"の良い補間メソッドです。

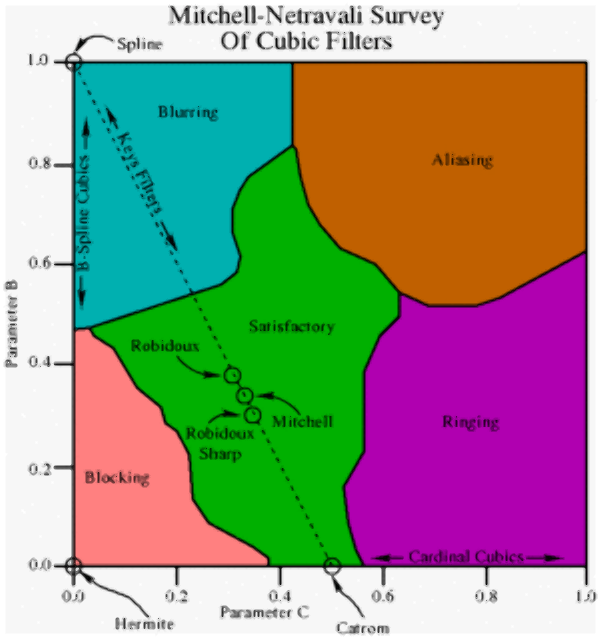
2つの自由度があり、B (Basis?),C(Cardinal) パラメータを組み合わせる事で、色んなフィルタを作り出せます。Cubic Family という呼び方もされます。

代表的な Cubic フィルタを並べます。

Hermite B:0, C:0	General B:1, C:0

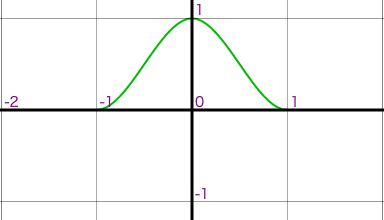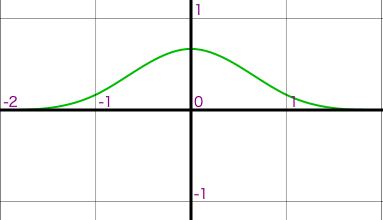Catmull-Rom B:0, C:1/2	Mitchell B:1/3, C:1/3

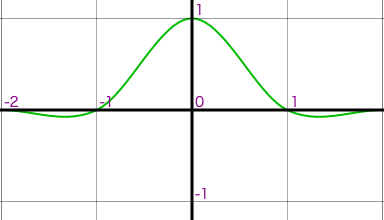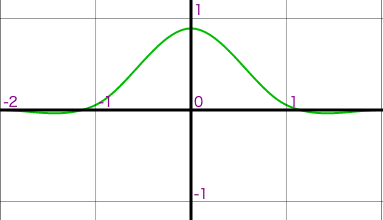なお、実験にて Mitchell がバランスが良いとされてます。


転載元) http://www.imagemagick.org/Usage/filter/#mitchell - 論文

計算方法

まず B,C を元に3次方程式の係数を算出します。

function cubicBCcoefficient(b, c) {
    var p = 2 - 1.5*b - c;
    var q = -3 + 2*b + c;
    var r = 0;
    var s = 1 - (1/3)*b;
    var t = -(1/6)*b - c;
    var u = b + 5*c;
    var v = -2*b - 8*c;
    var w = (4/3)*b + 4*c;
    return [p, q, r, s, t, u, v, w];
}

この係数を使って Cubic の数列を計算できます。

function cubicBC(x, coeff) {
    var [p, q, r, s, t, u, v, w] = coeff;
    var y = 0;
    var ax = Math.abs(x);
    if (ax < 1) {
      //y = p*(ax*ax*ax) + q*(ax*ax) + r*(ax) + s;
        y = ((p*ax + q)*ax + r)*ax + s;
    } else if (ax < 2) {
      //y = t*(ax*ax*ax) + u*(ax*ax) + v*(ax) + w;
        y = ((t*ax + u)*ax + v)*ax + w;
    }
    return y;
}

Lanczos lobeパラメータ

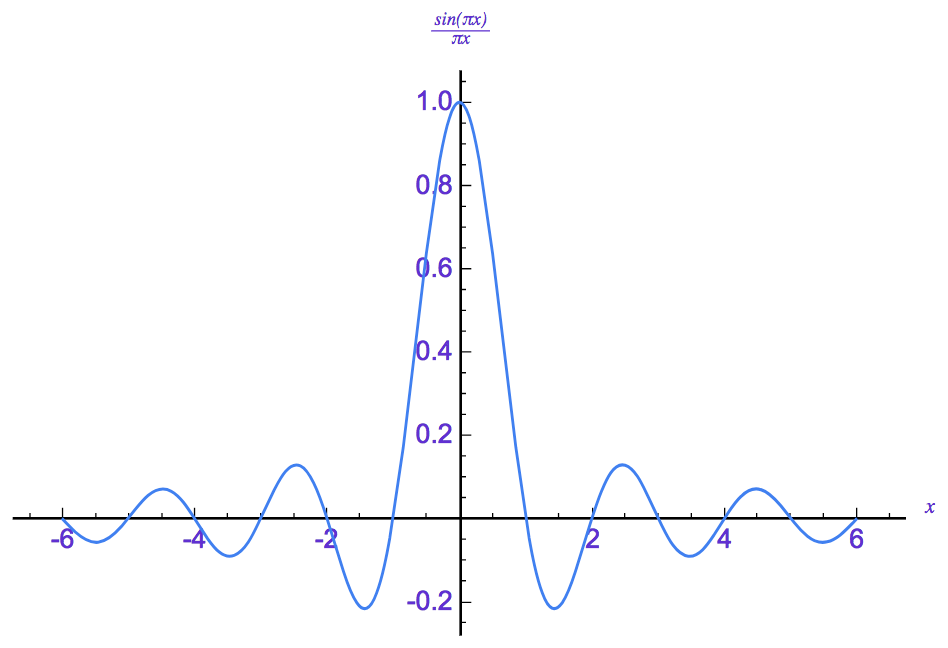
信号処理で大変便利な Sinc 窓というものがあります。


(c) https://en.wikipedia.org/wiki/Sinc_filter

これは永遠に横(x軸方向)に広がる関数なので、更に

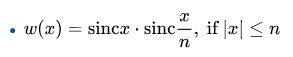
を計算することで、波の広がりを一定区間に抑えたのが Lanczos 窓です。

以下のグラフは分母の n が 2,3,4 の Lanczos 窓です。

lobe	グラフ
lobe:2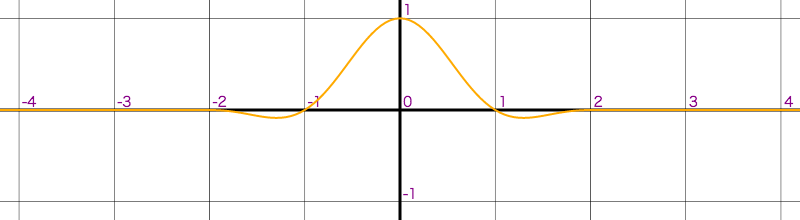
lobe:3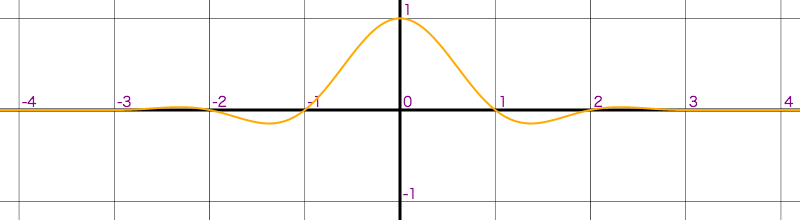
lobe:4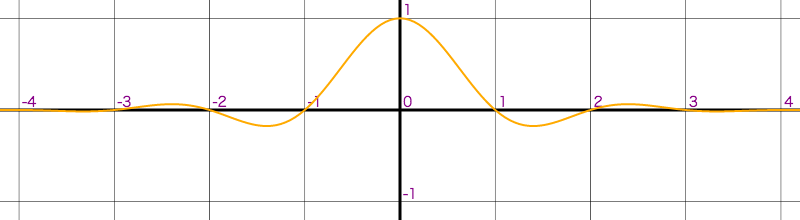

n でどこ区間まで波を広げるのか調整できます。パラメータ名として Lobe がよく使われるのと、n:3 を lanczos3, n:4 を lanczos4 のように呼称する事もあります。

Sinc は LPF(低域通過フィルタ)の性質もある為、Lanczos は縮小リサイズに向いています。ただし、sin関数を多用するのと実用的にカーネル窓を広めにとるので大変重たいメソッドです。

Lobe 値を増やすほど良い結果を期待できますが、その分処理が重たくなります。よく使われるのは Lobe:3 か 4 です。

計算方法

sinc は sin を使います。

function sinc(x) {
    var pi_x = Math.PI * x;
    return Math.sin(pi_x) / pi_x;
}

sinc 関数は無限に広がるので、そのまま使うと補間カーネルが無限の大きさを持ってしまいます。lanczos はこれを一定幅で抑える工夫をします。この一定区間に収まる事をコンパクトサポートといった表現をします。

function lanczos(x, lobe) {
    if (x === 0) {
        return 0;
    }
    if (Math.abs(x) < lobe) {
        return sinc(x) * sinc(x/lobe);
    }
    return 0;
}