はじめに
MSE/PSNR に比べて SSIM の方が見た目の差分をよく反映する典型的なケースを集めたドキュメントを紹介します。
- Mean Squared Error:Love It or Leave It? A New Look at Signal Fidelity Measures
Fig.4 まで注釈します。(参照先のドキュメントでは Fig.15 まであります)
前提知識
2つの画像がどの程度似ているかの定量化、画像類似度指標として特に有名なものとして、MSE/PSNR と SSIM があります。
MSE/PSNR
まず、2枚の画像の同じ位置同士のピクセル輝度差に abs をとって集計するのを思いつくでしょう。AE (Absolute Error) と呼びます。
AE = \sum^{m-1}_{i=0} \sum^{n-1}_{j=0} | I(i,j) - K(i,j) |
単純に足すと画像サイズにより値が変わるので、その平均を使うのが MAE (Mean Absolute Error) です。
MAE = \frac{1}{m \, n} \sum^{m-1}_{i=0} \sum^{n-1}_{j=0} | I(i,j) - K(i,j) |
この差分を二乗差にしたのが MSE (Mean Square Error) 。
MSE = \frac{1}{m \, n} \sum^{m-1}_{i=0} \sum^{n-1}_{j=0} [ I(i,j) - K(i,j) ]^2
更に差が大きすぎると鈍くなる人の目の感覚に近づけるよう $ \frac{MAX^2}{MSE} $ の(底が10の)対数をとって10乗算したのが PSNR (Peak Signal to Noise Ratio)です。PSNR の単位はデシベル(Db)です、
\begin{aligned}
PSNR &= 10 \cdot \log_{10} \left( \frac{MAX^2_I}{MSE} \right) \\
&= 20 \cdot \log_{10} \left( \frac{MAX_I}{\sqrt{MSE}} \right) \\
&= 20 \cdot \log_{10} (MAX_I) - 10 \cdot \log_{10}(MSE)
\end{aligned}
MSE/PSNR は単純に同じ位置のピクセル輝度値がどの位変わったのかを示します。
例えば全ピクセルが1つずれると見た目変わらないのに、MSE/PSNR は過敏に反応するといった分かりやすい欠点が色々とあります。
特に動画/画像コーデックのように、見た目の劣化が少ないよう工夫しながら、圧縮がよく効くように RGB 値を大胆に元の値から変化させていく。そんなケースとは相性がよくありません。
SSIM
輝度、コントラスト、構造に対して、ピクセル毎にその周囲の平均、分散、共分散をとることで、ピクセル単体のみならず、ピクセルの空間的な相関を取り込んだ指標です。
- SSIM index (とりあえず使える版)
SSIM(x,y) = \frac{(2 \mu_x \mu_y + c_1)(2 \sigma_{x y} + c_2)}{( \mu_x^2 + \mu_y^2 + c_1)( \sigma_x^2 + \sigma_y^2 + c_2)}
- SSIM (α、β、γパラメータを調整して使う)
SSIM(x,y) = [l(x,y)^{\alpha} \cdot c(x,y)^{\beta} \cdot s(x,y)^{\gamma} ]
\begin{aligned}
l(x,y) &= \frac{ 2 \mu_x \mu_y + c_1}{\mu_x^2 + \mu_y^2 + c_1} :輝度平均 \\
c(x,y) &= \frac{2 \sigma_x \sigma_y + c_2}{\sigma_x^2 + \sigma_y^2 + c_2} :輝度のばらつき \\
s(x,y) &= \frac{\sigma_{x y} + c_3}{\sigma_x \sigma_y + c_3} :輝度の偏り \\
\end{aligned}
(c) https://en.wikipedia.org/wiki/Structural_similarity
基本的にはブラーをかけた上で上記の計算を行います。
ピクセルずれへの過敏な反応は MSE/PSNRより抑えられますし、元々ごちゃったとした場所や高い輝度でマスクされる場所を人の目はあまり気にしないといった視覚特性も反映します。
MSE/PSNR より高度な画質評価のメジャーな方式です。
MSE/PSNR vs SSIM
さて、ここから本題で、MSE/PSNR と SSIM を比較した図です。
極端な例が多いですが、実際に MSE/PSNR だと見た目の差分と合わないケースがこれらで説明できる事もあります。
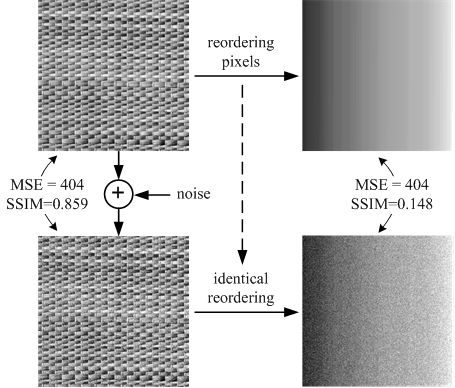
Fig.3(a)
- MSE:404 相当にノイズを全体的に混ぜる。(左上→左下の変換 - noize)
- 左ピクセルから暗>明の順に並び替える (左上→右上の変換 - reordering)
- 左上→右上と同じ手順で並び替える (左下→右下の変換 - identical reordering)
左のペアと右のペアは、どちらも MSE は 404 ですが画像の見た目の差分は全然違います。
平坦な場所ではノイズがより目立つ事が分かりやすい例です。
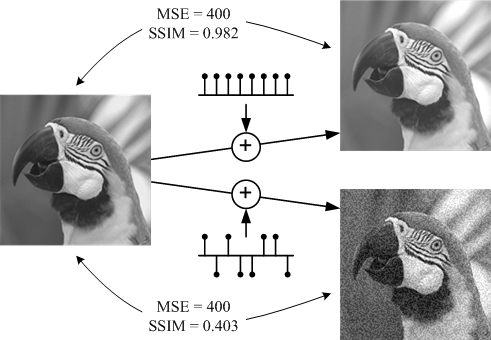
Fig.3(b)
画像の合成で MSE/PSNR が実態を表さないケースです。
- 元画像と相関の高い画像を合成する。(左)
- 元画像と相関の低い画像を合成する (右)
同じ画像を2つの異なる画像に合成した場合、それらの MSE は同一ですが、重ねる相手によってその違和感が全然異なります。
Fig.3(c)
- 均等に明るくする (左→右上)
- 明るくするのと暗くするのをランダムに入れる (左→右下)
全体を均等に明るくしても人の目は画質が悪くなったとは(あまり)思いませんが、明るい方向と暗くする方向の両方に費やすと MSE/PSNR は同じですが見た目は全然違ってきます。
Fig.3(d)
ヒートマップの白黒版です。全体的に均一にノイズを混ぜた場合。
Local absolute difference (MSE/PSNR 相当)だとそのまま全体に均一に差が出ますが、
Local SSIM では元々ノイズっぽい場所に新たなノイズが混ざっても気にならない一方、綺麗なグラデーション部分に混ざると目立つといった、人の目の性質に近い結果が出ます。
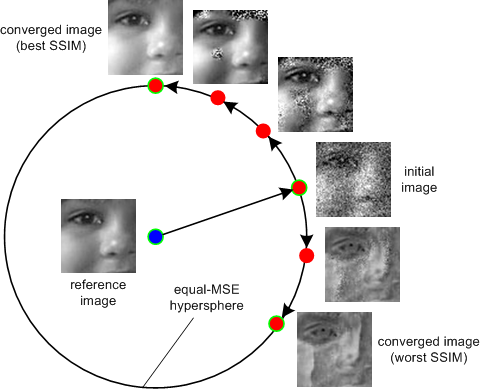
Fig.4
円周上の画像は全て MSE/PSNR だと同じ値になりますが、実際の見た目が全然違います。SSIM はこの見た目に相関した値を示します。
さいごに
Fig.5 〜 Fig.15 はもう少し理論的な話になるので、その解説は気が向いた時にでも。。
あと、SSIM も単純な統計量をとっている以上騙す事は出来ます。
苦手なケースもあるので、絶対的に信頼するのでなく、ひとつの方法として捉えるのが良いでしょう。
追記 (2018/10/04)
SSIM が苦手な画像が紹介されていたのでリンクを張ります。
SSIMは輝度・コントラスト・構造を元に類似度を数値化するということで、色相は軽視されているのかもしれません。
変換BのSSIM値が絶対的に高かったのは、輝度やコントラストには色相ほどの変化がなかったのではないかと推測します。
(無印)SSIM はグレースケール画像のアルゴリズムなので、カラー画像だと R,G,B を独立に SSIM 計算する事が多く、以下の右3つの画像に対する処理になります。
| 画像 | Red | Green | Blue |
|---|---|---|---|
 |
 |
 |
 |
 |
 |
 |
 |
SSIM の欠点として、グラデーションの違いを過小評価し過ぎる点があり、この画像の場合、階調を落とす事で生じる偽輪郭を差異として捉えているのですが、面積として占める割合が小さいので、結果として差異を小さく見積もってしまうようです。
あと、平均はともかく分散や共分散はガウス窓でブラーかける際の σ に強く影響されるので、デフォルト値がどうなってるのか気になります。