摩擦、空気抵抗のある最急降下曲線を求めようとして挫折した

#はじめに
ある日のこと、息子(3歳)がお風呂マットを壁に立てかけ、小銭を滑らせて遊んで研究していた。それを見て思った。
「この子はすごい。この年にしてもう最急降下曲線の問題に取り組んでいる!!」
最急降下曲線は摩擦や空気抵抗がない場合は簡単に導出できて(参考)、サイクロイドになることが知られている。でも、摩擦があるときの曲線がどうなるかなんて聞いたことがない。これはいつ息子に聞かれてもいいように考えておかなくては。
そういうわけで、摩擦・空気抵抗のある場合の最急降下曲線について考えることにした。

#問題設定
ある物体が位置O $(0,0)$ から斜面 $y=f(x)$ を滑り降りて位置G $(x_0,y_0)$ に到達する。この時、Gに至るまでにかかる時間が最短となる斜面はどのような曲線か。ただし $x_0>0, y_0<0$ 。

斜面に摩擦や空気抵抗がないときはよく知られているように、サイクロイドになる。
今回は、いつもは考えない摩擦や空気抵抗を考慮したらどのような曲線になるか考えることにする。
#解析計算
数学力に自信はないが、とりあえず摩擦・空気抵抗無しと同じように、変分法を使って計算しよう試みた。5分くらい考えてすっぱりあきらめ、Googleさんに聞いてみたところ、以下のサイトが出てきた。
http://takeno.iee.niit.ac.jp/~shige/math/lecture/misc/data/cycloid1.pdf
摩擦のある場合については、

摩擦のある場合は、摩擦のない場合の (11) の式のような、変分法が使える積分の式を導くことも容易ではない。

空気抵抗のある場合については、

これも (64) と同様にきれいには積分できない。k が定数でなく v の関数で
ある場合も、残念ながらあまりうまくいくような気はしない。

摩擦と空気抵抗がある場合は

摩擦と空気抵抗の両方を考えた式を作ることもできるが、それも簡単に解けそうな方程式にはならない。

というわけで、解析的に解くのは(数学力に自信のない自分にとって)絶望的。

#シミュレーション
解析的にうまくいかないならシミュレーション。

##運動方程式
運動方程式は

\begin{align}
m\ddot{x}&=
-\frac{f^{\prime}+\mu}{\sqrt{1+f^{\prime 2}}}N - k\dot{x},\\
m\ddot{y}&=
-\frac{1-\mu f^{\prime}}{\sqrt{1+f^{\prime 2}}}N - k\dot{y} - mg,
\end{align}

となる。変数の意味を一応コメントしておくと、$x$は重力と垂直方向、$y$は重力方向、$f$は斜面の形状を表す関数、$\mu$は摩擦係数、$N$は垂直抗力、$k$は空気抵抗の係数、$m$は物体の質量、$g$は重力加速度。

また斜面から離れない場合 $y(t)=f(x)$ なのだから、チェーンルールから

\begin{align}
\dot{y}&=\frac{dy}{dt}\\
&=\frac{df}{dx}\frac{dx}{dt}\\
&=f^{\prime}\dot{x}
\end{align}

同様にして
$$
\ddot{y}=f^{\prime\prime}\dot{x}^2+f^{\prime}\ddot{x}
$$
これらを使って$N,y$を消去&整理すると
$$
\ddot{x}=-\frac{\mu+f^{\prime}}{1+f^{\prime 2}}f^{\prime\prime}\dot{x}^2-\frac{k}{m}\frac{1+\mu f^{\prime}+f^{\prime 2}}{1+f^{\prime 2}}\dot{x}-\frac{\mu+f^{\prime}}{1+f^{\prime 2}}g
$$
細かいことを言うと$N$は斜面に接していない場合は$0$にしなければならないけど、問題設定的にそういう解はないので、無視する。答えが出た後で確認はしておいた方がいいかもしれない。

##斜面の表現方法
位置O$(0,0)$から出発して位置G$(x_0,y_0)$に到達するまでの時刻を最小にするように$f(x)$の値をいたるところで変化させるのが愚直な方法だが、$f$の微分があるし、補間するのもめんどくさそうだ。なにより、関数の形状がわかりにくい。そこで、Fourier展開で表現することにする。

位置Oと位置Gを通る曲線$f$は以下のように書ける。
$$
f(x) = \frac{y_0}{x_0}x + \sum_{n=1}^p a_n\cos\left(\frac{n\pi}{x_0}x\right) + \sum_{m=1}^q b_m\sin\left(\frac{m\pi}{x_0}x\right)
$$
ただし、$p$が偶数の時は

\begin{align}
a_p &= -\sum_{n=odd}a_n \\
a_{p-1} &= -\sum_{n=even}a_n
\end{align}

奇数の時は

\begin{align}
a_p &= -\sum_{n=even}a_n \\
a_{p-1} &= -\sum_{n=odd}a_n
\end{align}

を満たす必要がある。(条件を制限しすぎているかもしれない)この制限は当然ながら $x=0$ および $x=x_0$ で第2、第3項が０になるという条件からきている。
この表現を使って

\begin{align}
\frac{df}{dx}&=
\frac{y_0}{x_0}
-\sum_{n=1}^{p}\frac{a_nn\pi}{x_0}\sin\left(\frac{n\pi}{x_0}x\right)
+\sum_{n=1}^{q}\frac{b_nn\pi}{x_0}\cos\left(\frac{n\pi}{x_0}x\right) \\
\frac{d^2f}{dx^2}&=
-\sum_{n=1}^{p}\frac{a_nn^2\pi^2}{x_0^2}\cos\left(\frac{n\pi}{x_0}x\right)
-\sum_{n=1}^{q}\frac{b_nn^2\pi^2}{x_0^2}\sin\left(\frac{n\pi}{x_0}x\right)
\end{align}

と微分表現も解析的にわかるので、圧倒的にお手軽になる。

##ソースコード
###下準備

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint 

c_cycle=("#ea5415","#005192","#ffdf00","#1d7a21","#88593b","#737061")

必要なモジュールをインポート。使いこなせていないnumpyと、描画用のmatplotlibと微分方程式を簡単に解けるodeint。
c_cycleはなんとなく使っているミッフィーちゃんのカラーリング。

###斜面用の関数

def sin_series(coeffs, period, x):
    value_at_x = 0
    for i in range(len(coeffs)):
        value_at_x += coeffs[i]*np.sin(np.pi*(i+1)*x/period)
    return value_at_x

def cos_series(coeffs, period, x):
    value_at_x = 0
    for i in range(len(coeffs)):
        value_at_x += coeffs[i]*np.cos(np.pi*(i+1)*x/period)
    return value_at_x

# a curve through (0,0) and (goal_x,goal_y)
def func(sin_coeff, cos_coeff, goal_x, goal_y, x):
    return goal_y/goal_x*x + sin_series(sin_coeff, goal_x, x) + cos_series(cos_coeff, goal_x, x)

# 1st-derivertive of func
def d_func(sin_coeff, cos_coeff, goal_x, goal_y, x):
    new_sin_coeff = [] 
    new_cos_coeff = [] 
    for i in range(len(sin_coeff)):
        new_sin_coeff.append(sin_coeff[i]*(i+1)*np.pi/goal_x)
    for i in range(len(cos_coeff)):
        new_cos_coeff.append(-cos_coeff[i]*(i+1)*np.pi/goal_x)
    return goal_y/goal_x + cos_series(np.array(new_sin_coeff),goal_x,x) + sin_series(np.array(new_cos_coeff),goal_x,x)

#2nd-derivertive of func
def d2_func(sin_coeff, cos_coeff, goal_x, goal_y, x):
    new_sin_coeff = [] 
    new_cos_coeff = [] 
    for i in range(len(sin_coeff)):
        new_sin_coeff.append(-sin_coeff[i]*(i+1)*(i+1)*np.pi*np.pi/(goal_x*goal_x))
    for i in range(len(cos_coeff)):
        new_cos_coeff.append(-cos_coeff[i]*(i+1)*(i+1)*np.pi*np.pi/(goal_x*goal_x))
    return sin_series(np.array(new_sin_coeff),goal_x,x) + cos_series(np.array(new_cos_coeff),goal_x,x)

def extend_cos_coeff(cos_coeff):
    cos_coeff_odd  = sum(cos_coeff[0::2])
    cos_coeff_even = sum(cos_coeff[1::2])    
    if len(cos_coeff)%2==0:
        cos_coeff.append(-cos_coeff_odd)
        cos_coeff.append(-cos_coeff_even)
    else:
        cos_coeff.append(-cos_coeff_even)
        cos_coeff.append(-cos_coeff_odd)
    return np.array(cos_coeff)

特に説明はいらないと思う。斜面の表現で書いた数式をソースにしているだけ。for文を回して頑張るのがいけてない。

def equation_of_motion(state, simulation_time, sin_coeff, cos_coeff, goal_x, goal_y, m, mu, k, g):
    x, v = state
    fp   = d_func(sin_coeff, cos_coeff,goal_x,goal_y,x)
    f2p  = d2_func(sin_coeff, cos_coeff,goal_x,goal_y,x)
    temp = 1.0/(1+fp*fp)
    kp   = k/m
    mufp = mu+fp
    
    dxdt = [v, - temp*mufp*f2p*v*v - temp*kp*(1+mufp*fp)*v - temp*mufp*g  ]
    return dxdt

def get_result(phase_space, goal_x, goal_y, sin_coeff, cos_coeff, simulation_time):
    temp   = phase_space[phase_space[:,0]<goal_x]
    trajectory_x = temp[:,0]
    trajectory_y = np.array( list(map(lambda u: func(sin_coeff, cos_coeff, goal_x, goal_y, u), trajectory_x)) )
    time = simulation_time[:len(temp)]
    return trajectory_x, trajectory_y, time

運動方程式を解く部分と、ゴールに到達した時刻、それまでの軌跡を返す部分。運動方程式を解く部分はodeint用に書いてある。

#parameters
g      = 9.8 # gravity constant [m/s^2]
k      = 0.   # air resistance coefficient
mu     = 0.   # friction constant coeffici ent
mass   = 1   # mass [kg]
initial_state  = [0.0, 0.0] #x0,v0

simulation_time   = np.linspace(0, 2, (2*1000)+1) # time array

#define slope
goal_x  = 1
goal_y  = -1

for idx in range(5):
    sin_coeff = (np.random.rand(5)-0.5)*0.1
    cos_coeff = (np.random.rand(5)-0.5)*0.1
    cos_coeff = list(cos_coeff)
    cos_coeff = extend_cos_coeff(cos_coeff)

    #solve equation of motion
    phase_space = odeint(equation_of_motion, initial_state, simulation_time, args=(sin_coeff, cos_coeff, goal_x, goal_y, mass, mu, k, g))
    trajectory_x, trajectory_y, time = get_result(phase_space, goal_x, goal_y, sin_coeff, cos_coeff, simulation_time)

    #visualize
    plt.plot(trajectory_x[::10], trajectory_y[::10], ".", label='t={:.3f}'.format(time[-1]), markersize=10, color=c_cycle[idx])
plt.legend(loc='best')

動作確認用のコード。実行すると例えばこんな感じになる。

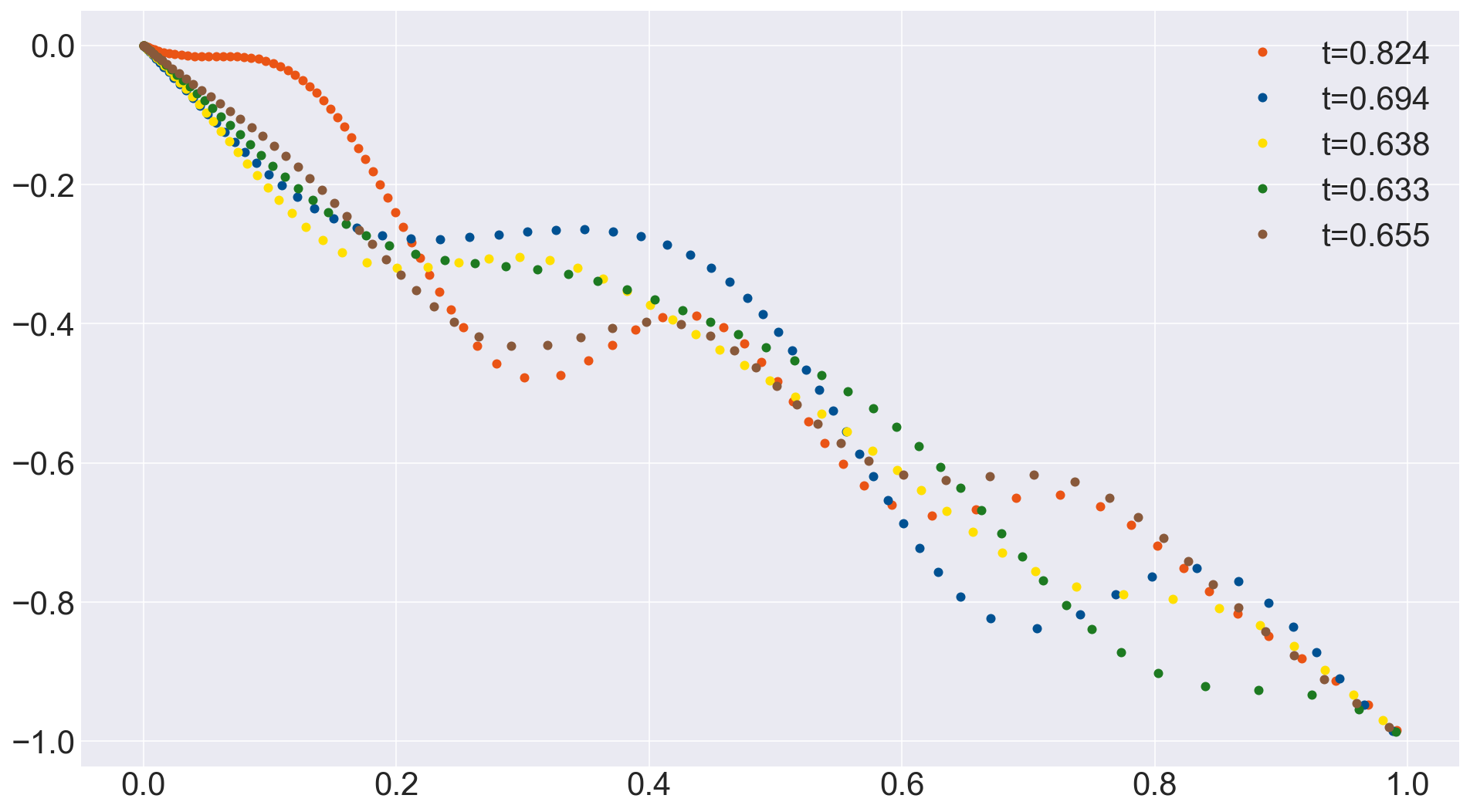
これだと緑の斜面が一番速いという結果だが、多分もっといい斜面があるのだろう。

#今後の展開
ここまでで、斜面の形状 $\{a_n\}, \{b_n\}$ を与えたら到着時刻 $t_{arrive}$ が得られる形になったので、機械学習で $\{a_n\}, \{b_n\}$ を入力に $t_{arrive}$ を最小化すればいいはず。
この後を引き継げる人がいたらだれかお願いします。

#追記(2019.5.13)
少し最適化してみました。
https://qiita.com/youiida/items/4b10fd878a6bf9876af3