「変動が激しい相場ではレバレッジ型投資信託が不利」という主張について金融工学で検証した

最近Twitterで，タイトルのような主張を見かけました．
基本的にこのような主張は疑わしいのですが，日本取引所グループの記事 (https://www.jpx.co.jp/equities/products/etfs/etf-outline/04-04.html) にも同様の主張があり，ある程度信憑性はあるかもしれないと思いました．本記事の目的は，この主張を金融工学的な観点から検証することです．そのため数理的な側面が強く，実際にお金を増やすという目的にはそぐわないということに注意してください．また，筆者は金融工学を勉強中の身ですので，何か不十分な点などあればご指摘願います．

レバレッジ型投資信託とは

レバレッジ型投資信託を理解するにあたっては，上述の記事が参考になると思います．
簡単に述べると，レバレッジ($r$倍)指標とは日々の変動率(リターン)に$r$倍の比率を掛けたリターンが得られるような指標です．
例えば，TOPIXが100ポイントから110ポイントになったとすると(+10%の変動)，TOPIXレバレッジ(2倍)指標は+20%の変動をします．そのため，原指標(ここではTOPIX)に投資するよりも大きなリターンを狙うことができる反面，マイナスの変動にも同様のレバレッジ効果が働くためリスクも抱えることになります．

タイトルの主張は，上述の記事では以下の画像のように説明されています．
確かに，この場合ではレバレッジ型のパフォーマンスが逓減されていることが確認できます．

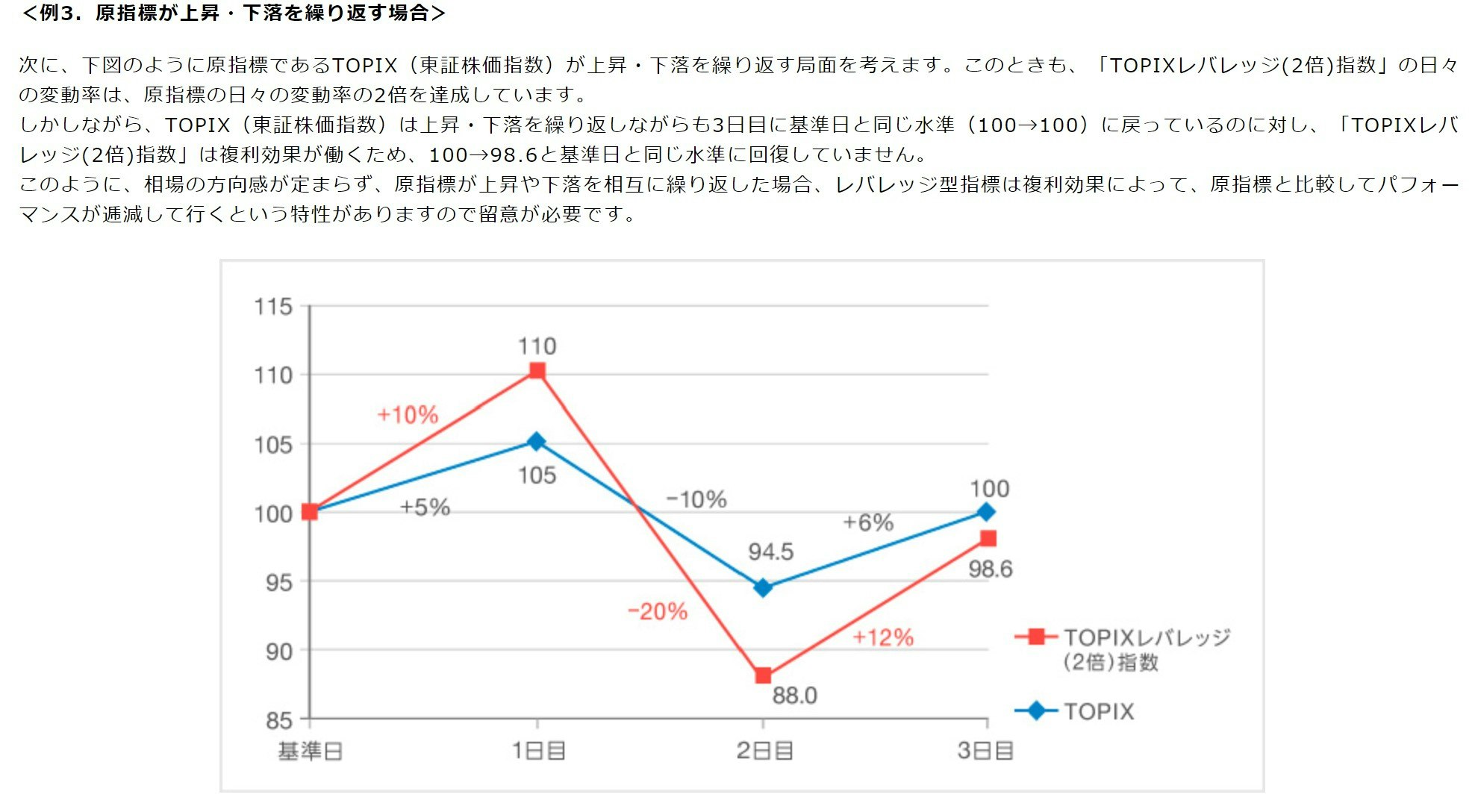
ただし，この説明を受けても以下のような不満がありました．

• サンプルパスが1つしかないため，たまたまパフォーマンスが逓減しただけかもしれない
• 原指標の変動がどのくらい激しいならばパフォーマンスが下がるのかについて記述がない

本記事では，これらに解答を与えることを目標とします．

数理モデル化

金融工学でよく用いられる幾何ブラウン運動により，以上の現象をモデル化しようと思います．
一般に，TOPIXなどの金融指標は以下のような幾何ブラウン運動でモデル化できることが知られています：

$$
dS_t = \mu S_t dt + \sigma S_t dW_t
$$
ただし$S_t$は金融指標，$\mu$は期待収益率，$\sigma$は変動率，$dW_t$はブラウン運動の増分を表しています．$dW_t$については，雑に述べると$dW_t \sim \mathcal{N} (0,\sqrt{dt})$に従うような乱数と言えます(正確な記述は金融工学の教科書を参照してください)．
この確率微分方程式を離散化する方法として，最も単純なのは以下のような方法でしょう：
$$
S_n = (1 + \mu \Delta t + \sigma \sqrt{\Delta t} \xi_n )S_{n-1}
$$
ただし$S_n$は時刻$n$における指標，$\Delta t$は離散化したタイムステップ，$\xi_n$は標準正規分布に従う乱数です．
ここでタイムスケールとしては1年程度を考えることにし，タイムステップ$\Delta t$としては1日程度の時間を扱います．つまり$\Delta t \simeq 1/360$程度とします．
このとき，レバレッジ($r$倍)指標の変動を$R_t$とすると，その定義から以下のようにモデル化することができます：
$$
R_n = (1 + r \mu \Delta t + r \sigma \sqrt{\Delta t} \xi_n) R_{n-1}
$$
このモデル化により，確かに日次リターンが$r$倍されていることが確認できます．
また，期待収益率$\mu$と変動率$\sigma$をそれぞれ$r$倍したことと同様であることに注意してください．明らかですが，$r=1$は原指標に対応します．

さらに，原指標について解析解が求められることにも注意します：
$$
S_t = S_0 \exp [ (\mu - \sigma^2/2) t + \sigma W_t]
$$
またその確率分布$p(S)$については以下のように対数正規分布に従います：
$$
p(S) = \dfrac{S_0}{\sqrt{2 \pi \sigma^2 t} S} \exp \left[ -\dfrac{1}{2\sigma^2 t} (\log S/S_0 - (\mu - \sigma^2/2)t )^2 \right]
$$

シミュレーションによる確認

いくつかのパラメータについて，jupyterで簡単にシミュレーションを行い確認しました．
シミュレーションの条件としては，初期値を$S_0 = 100$とし期待収益率$\mu = 1.0$で固定の下で$8000$回シミュレーションを行い，$\sigma$の値を変更しています．細かい部分はコードを参照してください．また結果の確認のために解析解(対数正規分布)も併せて示しています．



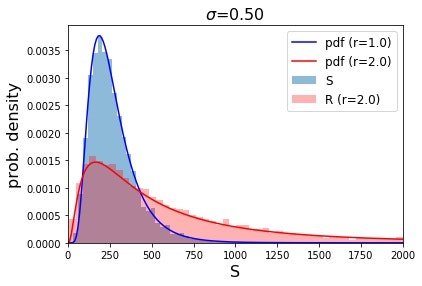
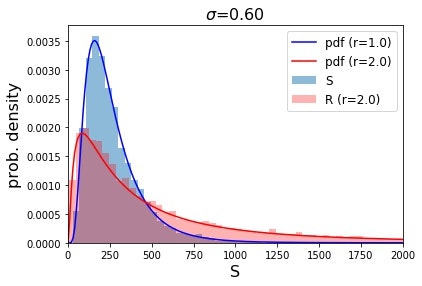
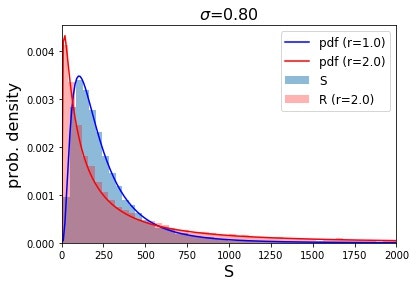
図から明らかなように，変動率$\sigma$が大きくなるとレバレッジ型$R$の確率分布が左に寄る，つまりパフォーマンスが悪くなります．よって変動が激しい相場ではレバレッジ型が不利になるという主張を確認することができました．
一応コードも示しておきます．グラフのプロット部分は本質的ではないので省略します．

シミュレーションのためのコード

mu = 1.0 # 期待収益率
sigma = 0.8 # 変動率
T = 1.0 # 1 year
days = 365 # 1 day
dt = 1.0 / days # ステップサイズ

S0 = 100.0 # 初期条件
num_sample = 8000 # サンプルパスの数
S_data = np.zeros(num_sample) # 原指標のデータ
R_data = np.zeros(num_sample) # レバレッジ型指標(r倍)のデータ
r = 2.0 # レバレッジ型が何倍か

for i in range(num_sample):
    S = S0
    R = S0 # 初期条件はそろえる
    for d in range(days):
        xi = np.random.randn()
        S = S*(1.0 + mu*dt + sigma*xi*np.sqrt(dt))
        R = R*(1.0 + r*(mu*dt + sigma*xi*np.sqrt(dt)))
    S_data[i] = S
    R_data[i] = R

def lognormal(S, S0, mu, sigma, T):
    return np.exp(-((np.log(S/S0) - (mu-0.5*sigma*sigma)*T)**2.0) / (2.0*sigma*sigma*T) ) / (np.sqrt(2.0*np.pi*sigma*sigma*T)*S)
pdf_S = lognormal(S_grid, S0, mu, sigma, T)
pdf_R = lognormal(S_grid, S0, mu*r, sigma*r, T)

レバレッジ型投資信託が"不利"になるための条件

冒頭の二つの疑問のうち，片方について(つまり多くのサンプルパスに対する確認)は達成できましたが，もう一方について(つまりレバレッジ型が"不利"となる条件)についてはまた詳しくわかっていません．
そこで，レバレッジ型投資信託が"不利"となることを以下のように定義します：
**
レバレッジ($r$倍)指標が"不利"であるとは，時刻$T$までその指標を保有していた場合，原指標よりも値が小さくなる確率$p$が$1/2$を越えるということである．
**
(この定義についてはいまいちかもしれません．より良い定義の仕方があれば教えてもらいたいです．)

いま，レバレッジ($r$倍指標)の確率微分方程式は，原指標の確率微分方程式において期待収益率$\mu$と変動率$\sigma$をそれぞれ$r$倍すればよいということがわかっています．
また，原指標の確率微分方程式に対しては解析解が求められるため，リスク・リターン平面(つまりパラメータ$\mu$，$\sigma$の平面)において，$r$の値ごとにレバレッジ型が"不利"となる領域を見出すことができます．
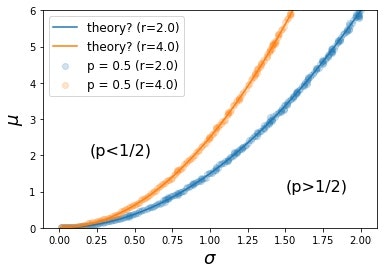
以上に基づき，レバレッジ型($r$倍指標)が時刻$T$において，原指標よりも値が小さくなる確率$p$が$1/2$となる境界線を示したものが下図です．

この図から，期待収益率$\mu$が一定である場合，変動率$\sigma$が大きくなると，"不利"となることがやはり確認できます．
さらに，$r$が大きくなるとその傾向はより顕著になることも分かります．つまり，レバレッジ型投資信託が"不利"となる領域($p>1/2$となる領域)が広がることも確認できます．
以上から，やはりレバレッジ型投資信託は変動が激しい相場で"不利"となることが確かめられました．特に，市場の状況$\mu$，$\sigma$に応じて"有利・不利"を決定できたことに注意してください．
なお，図の"theory"は以下のようにして計算しました．原指標$S_t$の解析解と同様に，レバレッジ型($r$倍)指標も解析解を求めることができます：
$$
R_t = S_0 \exp [ (r \mu - r^2 \sigma^2 /2) t + r \sigma W_t ]
$$
指数部分の$t$の係数を$S_t$と$R_t$で比較したとき，これらが等しくなるという条件は以下のようになります：
$$
\mu = \dfrac{1}{2}(1+r) \sigma^2
$$
これを$r$の値ごとにプロットしたものが図の"theory"になります．グラフから，これが$p = 1/2$の境界線を非常によく説明していることがわかりますが，なぜこれで説明できるのかはまだわかっていません．
申し訳程度のコードを示します．グラフを出力する部分は省略．

import numpy as np
from scipy.stats import lognorm
import matplotlib.pyplot as plt

S0 = 100
T = 1.0 # 1 year
r1 = 2.0
r2 = 4.0
num_sample = 2000

num_grid_param = 200
mu_start = 0.0
mu_end = 6.0
mu_list = np.linspace(mu_start, mu_end, num_grid_param)
sigma_start = 0.01
sigma_end = 2.0
sigma_list = np.linspace(sigma_start, sigma_end, num_grid_param)

params_critical1 = []
params_critical2 = []

def calc_params_critical(r):
    params_critical = []
    for sigma in sigma_list:
        print("sigma = {:.3f}".format(sigma), end = "\r")
        for mu in mu_list:
            B = np.random.randn(num_sample)*np.sqrt(T)
            S = S0*np.exp((mu-sigma*sigma*0.5)*T + sigma*B)

            mu_r, sigma_r = r*mu, r*sigma
            R = S0*np.exp((mu_r-sigma_r*sigma_r*0.5)*T + sigma_r*B)
            prob = sum(R < S) / num_sample # レバレッジ型のパフォーマンスが劣る確率

            if mu == mu_start:
                prob_old = prob
            else:
                if (prob-0.5)*(prob_old-0.5) < 0.0:
                    params_critical.append([sigma,mu])
                prob_old = prob
    params_critical = np.array(params_critical)
    return params_critical

params_critical1 = calc_params_critical(r1)
params_critical2 = calc_params_critical(r2)

まとめと注意

簡単なモデル化により，「変動が激しい相場ではレバレッジ型投資信託が不利となる」という主張を検証しました．
結果として，このモデル化の下では主張が正しいことが確かめられました．
また，"不利"について適当な定義をすることで，市場の状況を表す期待収益率$\mu$，変動率$\sigma$の値ごとに"有利・不利"を定量的に決定することができました．
特に，レバレッジの比率$r$が大きくなると"不利"となる領域が広がることも確認できました．これは，冒頭の主張の正当性を示すものと考えられます．
さらに，解析解の指数部分を比較することによりその境界線$p = 1/2$の解析解を求められました．

以上の解析は，数理的なアプローチに終始していることに注意してください．日次リターンの分布などから$\mu,\sigma$を求めるともっと面白いことが言えるかもしれませんが，あまり興味がないので手を付けないことにします．また，実際のTOPIXのデータを使って検証しても面白いかもしれませんが，面倒なので気が向いたらやることにします．