蔵本モデルの高速計算

　
蔵本モデルは同期現象を説明する数理モデルです。例えばホタルがタイミングをそろえて発光するような現象も同期現象であり、蔵本モデルによって説明されます。
このモデルにおいては多数の振動子の時間発展を考えることになりますが、当然厳密に解くことは不可能なので数値計算を行います。このときうまい工夫をすれば計算量を落とすことが出来るということを教えてもらったので、ここに書き残したいと思います。

1 蔵本モデルについて

まず蔵本モデルの説明と理論的解析、および数値計算の結果結果を示します。

1.1 蔵本モデルの説明

蔵本モデルは$N$個の振動子$\theta_i$が以下のような時間発展をする系です：

\dfrac{d \theta_i}{dt} = \omega_i -\dfrac{K}{N} \sum_j \sin(\theta_i-\theta_j)

第一項は各振動子の持つ固有振動数を表しており、これは確率分布$g(\omega)$に従うものとします。一般的な設定では、$g(\omega)$はGauss分布やCauchy分布を仮定することが多いです。
第二項は振動子間の引き合う力を表しています。結合強度$K$が大きい程、各振動子は位相をそろえようとすると考えられます。
今回はノイズを含まない系を扱うことにしましょう。

1.2 理論的解析の結果

この系の解析を行うために、以下のような秩序パラメータを導入することにします：

R(t) = \left| \dfrac{1}{N} \sum_j e^{i \theta_j (t)} \right| \\
\Theta(t) = {\rm Arg} \left[ \dfrac{1}{N} \sum_j e^{i \theta_j (t)} \right]

位相がそろっている同期状態であれば、$R(t)$が$1$に近くなるということがイメージできると思います。また位相がばらけている状態では$R(t)$は$0$に近くなります。$\dfrac{1}{N} \sum_j e^{i \theta_j} = R(t) e^{i\Theta}$が成立することに注意します。
さらに具体的な解析を行うために、自然振動数$\omega$はCauchy分布に従うものとします：

g(\omega) = \dfrac{1}{\pi} \dfrac{ \gamma}{(\omega-\omega_0)^2+\gamma^2}

ここで$\omega_0$は分布の中心、$\gamma$は分布の広がりを表すパラメーターです。
このとき、秩序変数$R(t)$の平衡状態での値$R_{\infty}$は、結合強度$K$と自然振動数の分布の広がり$\gamma$だけを用いて以下のように書けることが知られています：

R_{\infty} = \sqrt{ 1- \dfrac{2 \gamma}{K} }

ただしこの式は$K > K_{\rm c} = 2 \gamma$のときのみ成立し、$K < K_{\rm c}$のときは$R_{\infty} = 0$となります。この式の物理的意味は明らかです。つまり固有振動数がばらばらである(つまり$\gamma$が大きい)ほど位相はそろいにくいですが、それに打ち勝つほどの結合強度$K$であれば位相はそろい、同期する($R_{\infty}>0$)ということです。
また統計力学を学んでいれば、この現象は二次相転移であるということにも気が付きます。非常に興味深いことに、固有振動数の分布$g(\omega)$の形によっては一次相転移になることもあります。

1.3 数値シミュレーション結果

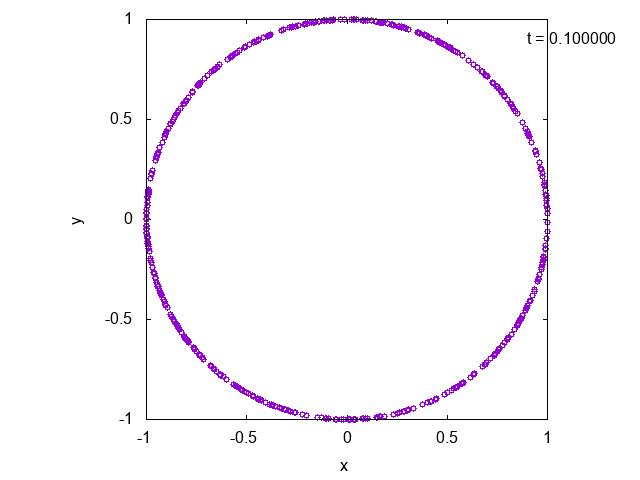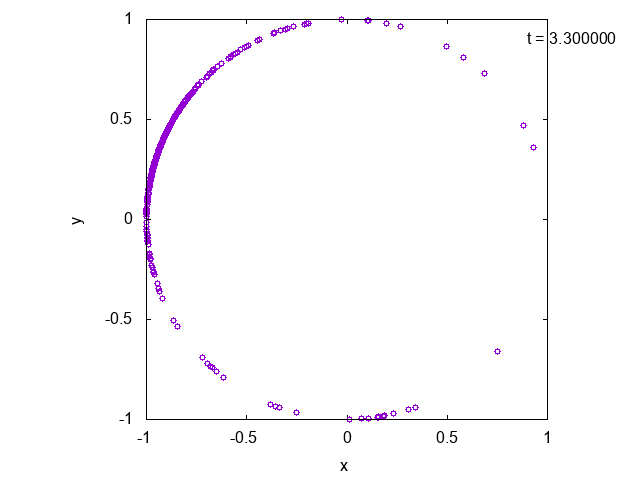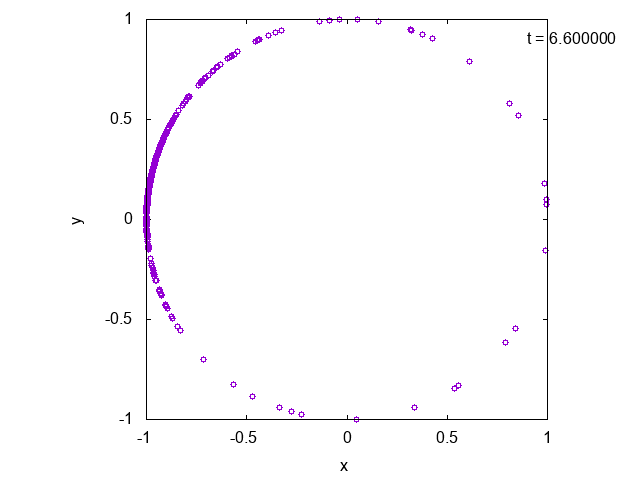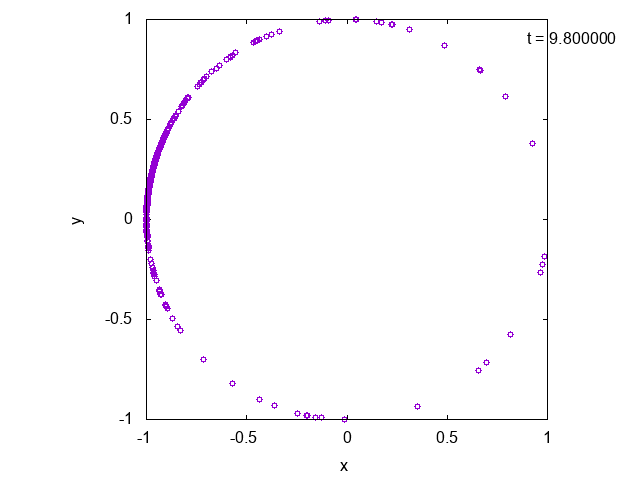
先ほどのモデルに基づいてシミュレーションした結果を以下に示します。位相のダイナミクスを円周上の運動として表現しています。時間が経つと徐々に位相がそろっていることが確認できます。

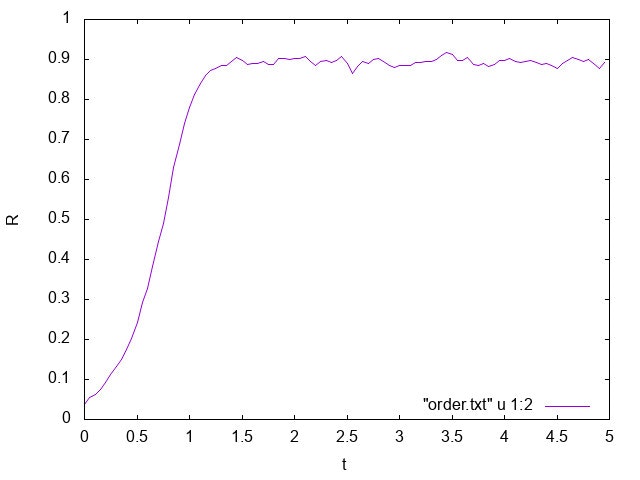
さらに秩序変数$R(t)$の時間変化を以下に示します。十分時間が経過すると位相がそろうことが定量的にも分かります。

なお、計算に用いたパラメータは$K=10.0,~\gamma = 1.0,~\omega_0 = 4.0$です。振動子数は$N=500$としました。

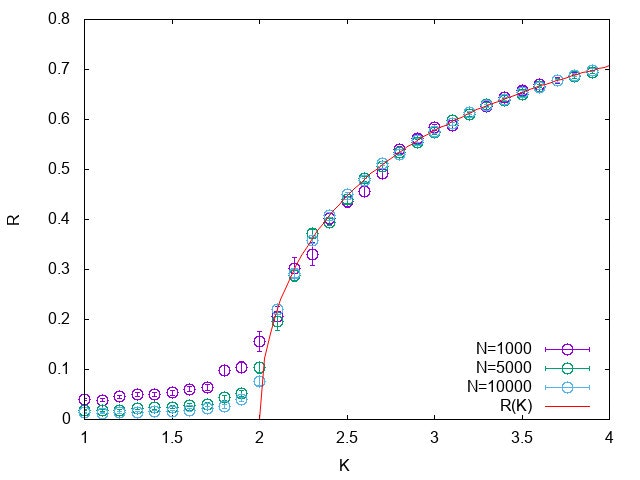
また$\gamma = 1.0$において結合強度$K$を様々に変えることで、平衡状態での値$R_{\infty}$がどのように変化するかを示したものが下図です。たしかに$K \simeq K_{\rm c} = 2.0$の付近で二次相転移しています。また$R_{\infty}(K)$を赤線で示しましたが、シミュレーションと非常に良い一致を示しています。

以下ではこのようなシミュレーションを行う際の実装を示し、計算の工夫をすることで計算量が改善されることを見ます。

2 素朴な実装

さきほどの微分方程式を考えると、素朴にEuler前進差分を適用すれば以下のようになるでしょう。時間発展部分だけを示します。一時保存用の配列としてthetanew[N+1]を用いていることに注意してください。

蔵本モデル(時間発展部分)

    for(int i=1;i<=N;i++){
        thetanew[i] += omega[i]*dt;
    }
    for(int i=1;i<=N;i++){
        for(int j=1;j<=N;j++){
            thetanew[j] += -(K/(double)N)*sin(theta[i]-theta[j])*dt;
        }
    }
    for(int i=1;i<=N;i++){
        theta[i]=thetanew[i];
    }

このコードを見ればわかるように、1タイムステップ当たりの計算量は$\mathcal{O}(N^2)$です。しかし計算の工夫をすることにより、これを$\mathcal{O}(N)$にまで下げることが出来ます。

3 高速化

まず微分方程式の変形を示してから、計算量を削減できることを見ます。

3.1 微分方程式の変形

以下の変形に注意します：

\dfrac{1}{N} \sum_j \sin (\theta_i - \theta_j) = \dfrac{1}{N} \sum_j {\rm Im}~ e^{ i(\theta_i-\theta_j) } = {\rm Im}~ R e^{i(\theta_i - \Theta)} = R \sin( \theta_i - \Theta)

ただし途中で秩序変数の定義式 $R e^{i\Theta} = \dfrac{1}{N} \sum_j e^{i \theta_j}$を利用しました。
これを利用すると、蔵本モデルの微分方程式は以下のように変形されます：

\dfrac{d \theta_i}{dt} = \omega_i -KR \sin(\theta_i-\Theta)

秩序パラメータ$R,~\Theta$はともに$\mathcal{O}(N)$で計算できるので、あらかじめ秩序パラメータさえ計算していれば時間発展部分も$\mathcal{O}(N)$で計算できます。

3.2 実装

以上を踏まえたうえでの実装を示します。

蔵本モデル(高速化)

#include <stdio.h>
#include <math.h>
#include <stdlib.h>
#include <time.h>

#define N 500 //関数の定義のためにここに必要
double rand_cauchy( double mu, double gamma);
double Uniform(void);
double order(double theta[N+1]);//複素秩序変数の絶対値を計算する関数
double arg(double theta[N+1]);//複素秩序変数の偏角を計算する関数

int main(void){
    //fileの準備
    FILE *fp_gif,*fp_order;
    char name_txt[256],name_gif[256],name_order[256];
    sprintf(name_gif,"gif.txt");
    if((fp_gif = fopen(name_gif,"w"))==NULL){
        printf("file open error\n");
    }
    sprintf(name_order,"order.txt");
    if((fp_order = fopen(name_order,"w"))==NULL){
        printf("file open error\n");
    }

    int i,j,k;
    double pi = atan(1.0)*4.0;
    double theta[N+1],thetanew[N+1];
    double omega[N+1];//固有各振動数
    double K=10.0;//相関の強さを表す定数と刻み幅
    double t = 0.0,dt = 0.0010,trec=0.0,T = 5.0,dtrec=T/100.0;
    double R,Theta;
    double omega0 = 4.0,gamma = 1.0;
    srand((unsigned) time(NULL));
    //初期条件の設定
    for(i=1;i<=N;i++){
        theta[i]=2.0*pi*Uniform();
        thetanew[i]=theta[i];
        omega[i] = rand_cauchy(omega0,gamma);
    }
    R = order(theta);
    Theta = arg(theta);
    //file output
    fprintf(fp_order,"%lf %lf %lf\n",t,R,Theta);
    for(i=1;i<=N;i++){
        fprintf(fp_gif,"%lf %lf\n",cos(theta[i]),sin(theta[i]));
    }
    fprintf(fp_gif,"\n\n");

    //時間発展の計算
    while(t<=T){
        R = order(theta);
        Theta = arg(theta);
        for(i=1;i<=N;i++){
            thetanew[i] += omega[i]*dt;
            thetanew[i] += -K*R*sin(theta[i]-Theta)*dt;
        }
        for(i=1;i<=N;i++){
            theta[i]=thetanew[i];
        }

        //fileへの出力
        if(fabs(t-trec)<0.5*dt){
            R = order(theta);
            Theta = arg(theta);
            fprintf(fp_order,"%lf %lf %lf\n",t,R,Theta);
            for(i=1;i<=N;i++){
                fprintf(fp_gif,"%lf %lf\n",cos(theta[i]),sin(theta[i]));
            }
            fprintf(fp_gif,"\n\n");
            trec += dtrec;
            printf("t = %lf:%lf\n",t,R);
        }
        t+=dt;
    }
    fclose(fp_gif);
    fclose(fp_order);
    return 0;
}


double order(double theta[N+1]){
    double X=0.0,Y=0.0;
    for(int i=1;i<=N;i++){
        X += cos(theta[i])/(double)N;
        Y += sin(theta[i])/(double)N;
    }
    return sqrt(X*X+Y*Y);
}

double arg(double theta[N+1]){
    double X=0,Y=0;
    for(int i=1;i<=N;i++){
        X += cos(theta[i])/(double)N;
        Y += sin(theta[i])/(double)N;
    }
    return atan2(Y,X);
}


double Uniform(void){
    return ((double)rand()+1.0)/((double)RAND_MAX+2.0);
}

double rand_cauchy( double mu, double gamma){
    return mu + gamma*tan(M_PI*( Uniform()-0.5 ));
}

明らかに$\mathcal{O}(N)$になっています。蔵本モデルによる相転移では多くの粒子数を必要とするので、この計算量の削減は非常に効果的です。

4 結論

秩序変数を用いつつ微分方程式を変形することで、計算量を$\mathcal{O}(N^2)$から$\mathcal{O}(N)$に落とすことが出来ました。

5 おまけ

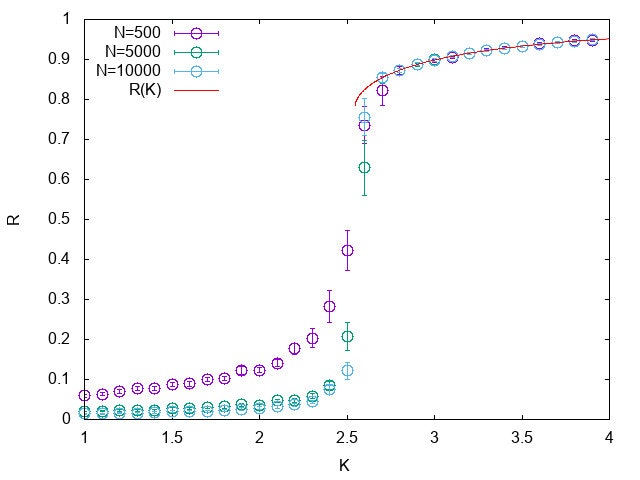
自然振動数の分布$g(\omega)$が$-\gamma$から$\gamma$まで一様分布する場合には一次相転移するようです。以下に$\gamma = 2.0$としたときのシミュレーション結果を示します。

実はこのときの平衡値$R$は以下のような自己無撞着方程式の解として得られます：

R = \dfrac{1}{2} \sqrt{ 1-\left( \dfrac{\gamma}{KR} \right)^2 }+ \dfrac{KR}{2\gamma} \sin^{-1} \left( \dfrac{\gamma}{KR} \right)

先ほどのシミュレーション結果にはこの自己無撞着方程式を解くことにより得られる$R(K)$も示しています。さらに臨界結合強度として$K_{\rm c} = \dfrac{4 \gamma}{\pi}$が得られます。実際に$\gamma = 2.0$を代入すると$K_{\rm c} \simeq 2.6$となり、シミュレーションによく一致します。