時系列データに対する回帰分析手法としてのカルマンフィルター

時系列データに対する回帰分析では，回帰係数が時間的に変化するような状況が想定されます．本記事では，このような場合にカルマンフィルターが適用できることを説明し，具体的な分析例を示します．具体的な実装（の一部）はGitHubにアップロードしています．

モチベーション

以下のように，時間的に変化する$y_t$を$x_t$に線形回帰するモデルを考えます．

y_t = \alpha + \beta x_t + \epsilon _ t

ただし$\epsilon _ t$は各時刻$t$で独立な乱数で，平均$0$，分散$\sigma^2$の正規分布に従います．例えば$x_t$を可処分所得，$y_t$を最終消費支出とすると，$\beta$は限界消費性向（可処分所得の増加に対する消費割合）を表します．線形回帰モデルでは回帰係数$\beta$（そして$\alpha$）が一定と仮定しますが，時間的に変化する以下のモデルを想定したい場合があります．

y_t = \alpha_t + \beta_t x_t + \epsilon _ t

以下では，このようなモデルを取り扱う方法としてカルマンフィルターを説明します．まずカルマンフィルターを定式化し，サンプルデータに対するpykalmanによる実装を示します．また具体例として，限界消費性向の時間変化を推定します．

カルマンフィルターの定式化

ここでは一般的に，時間的に変化する観測データ${\bf y}_t$と説明変数${\bf X}_t$をもとに，回帰係数${\boldsymbol \beta}_t$を推定する問題を考えます．具体的には，以下のようなモデルを想定します．

\displaylines{
{\boldsymbol \beta} _ {1} \sim \mathcal{N}({\boldsymbol \mu}, {\bf V}) \\ 

{\boldsymbol \beta} _ {t  + 1} = {\bf A} _ t {\boldsymbol \beta} _ {t} + {\bf b}_t + {\boldsymbol \xi} _ {t} 
, \quad
{\boldsymbol \xi} _ {t}  \sim \mathcal{N}({\bf 0}, \Gamma) \\ 

{\bf y}_{t} = {\bf X} _ t {\boldsymbol \beta} _ {t} + {\bf d}_t + {\boldsymbol \epsilon} _ {t} , \quad
{\boldsymbol \epsilon} _ {t}  \sim \mathcal{N}({\bf 0}, \Sigma) \\
}  

ここで導入した以下のパラメータは，一般的には未知のものとして取り扱います．

• ${\boldsymbol \beta} _ 1$の平均${\boldsymbol \mu}$および共分散行列${\bf V}$
• モデルのダイナミクスを決める${\bf A}_t$，${\bf b}_t$，${\bf d}_t$
• ノイズを特徴づける$\Gamma$，$\Sigma$

このうち最適化したいパラメータを${\boldsymbol \theta}$とすると，EMアルゴリズムによって尤度

\log p({\bf y}_1, \ldots, {\bf y}_T | {\boldsymbol \theta})

を高めるパラメータ${\boldsymbol \theta}$を求めることができます．その後，時刻$t$までの情報を所与とした回帰係数${\boldsymbol \beta}_t$の確率分布

 p({\boldsymbol \beta}_t | {\bf y}_1, \ldots, {\bf y}_t, {\boldsymbol \theta})

を計算します（フィルタリング）．また，全期間の情報を所与とした回帰係数${\boldsymbol \beta}_t$の確率分布

 p({\boldsymbol \beta}_t | {\bf y}_1, \ldots, {\bf y}_T, {\boldsymbol \theta})

を計算することもできます（スムージング）．ここではノイズが正規分布に従うという強い仮定があるため，（EMアルゴリズムを含め）解析的な計算が可能です．¹
実装には以下のようにpykalmanを使うことができます．ただしEMアルゴリズムで最適化するパラメータ${\boldsymbol \theta}$は，時間的に一定と仮定する必要があります．

kf = KalmanFilter(
    initial_state_mean = state_mean_initial, # \mu
    initial_state_covariance = state_covariance_initial, # V
    transition_matrices = transition_matrix_initial, # A_t
    transition_covariance = transition_covariance_initial, # \Gamma
    transition_offsets = 0, # b_t
    observation_matrices = df_sample["x"].values.reshape(-1, 1, 1), # X_t
    observation_covariance = observation_covariance_initial, # \Sigma
    observation_offsets = 0, # d_t
    em_vars = ["initial_state_mean", "initial_state_covariance", \
               "transition_covariance", "transition_matrices", "transition_offsets", \
               "observation_covariance", "observation_offsets"]
)

kf.em(df_sample["y"].values, n_iter = 100)   
filtered_state_means, filtered_state_covariances = kf.filter(df_sample["y"].values)
smoothing_state_means, smoothing_state_covariances = kf.smooth(df_sample["y"].values)

ここで，パラメータ${\bf A} _ t$および${\bf b} _ t$について直観的に理解するため，回帰係数${\boldsymbol \beta}_t$が$1$次元である

\beta _ {t  + 1} = a \beta _ {t} + b +  \xi  _ {t}

の場合を考えます($a_t = a, b_t = b$で一定と仮定)．このとき，回帰係数$\beta_t$の変化は

\Delta \beta _ {t + 1} = \beta _ {t  + 1} - \beta _ {t } = - (1 - a) \left(\beta _ {t} - \dfrac{b}{1 - a} \right)  +  \xi  _ {t} = - c (\beta _ {t} - \bar{\beta}) +  \xi  _ {t}

のように表現されます．ただし$\bar{\beta} = \dfrac{b}{1 - a}$と$c = 1 - a$は$\beta _ t$のダイナミクスを以下のように特徴づけます．

• $c > 0$ ($a < 1$)の場合，$\beta _ t$は$\bar{\beta}$に回帰する傾向を持つ
• $c = 0$ ($a = 1$)の場合，$b = 0$ならば$\beta _ t$はランダムウォーク，$b \neq 0$ならば$\beta _ t$は$b$の符号の方向にドリフトする
• $c < 0$ ($a > 1$)の場合，$\beta _ t$は$\bar{\beta}$から離れる傾向を持つ

特に回帰係数${\boldsymbol \beta}_t$のダイナミクスがわかっていない場合は，ランダムウォークであると仮定して$a = 1, b = 0$とすればよいでしょう．他のパラメータは取り扱う問題によって異なると想定されるため，ドメイン知識やデータをもとに適切に設定する必要があります．

EMアルゴリズムの収束先はパラメータ${\boldsymbol \theta}$の初期値によって異なるため，適切に設定することは意外と重要です．

サンプルデータでの分析

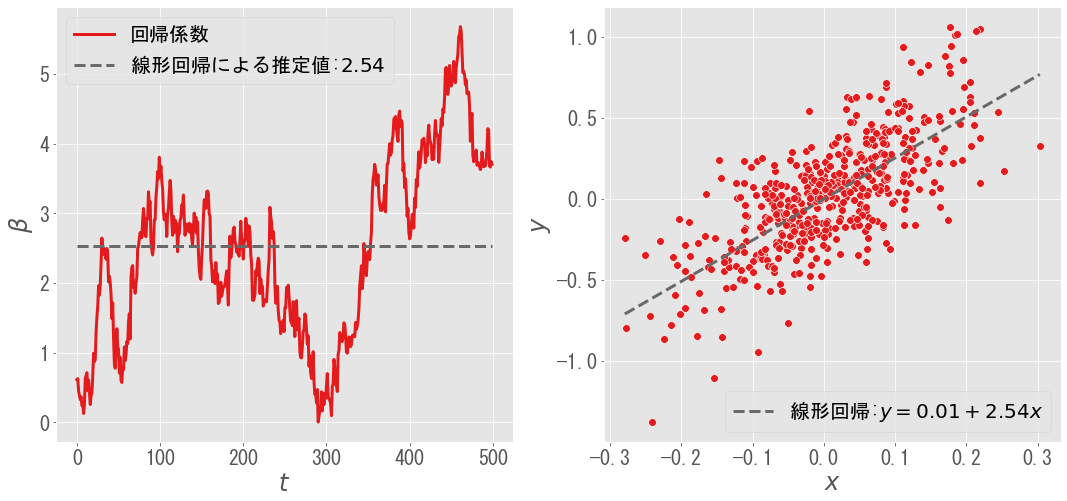
ここではサンプルとして，左図のようにランダムウォークする回帰係数$\beta _ t$を考えます（$\alpha _ t = 0$と仮定）．適当に説明変数$x _ t$を生成することで，右図のような観測データ$y$が得られます．左右の破線は，線形回帰による回帰係数の推定値および回帰直線を表しています．

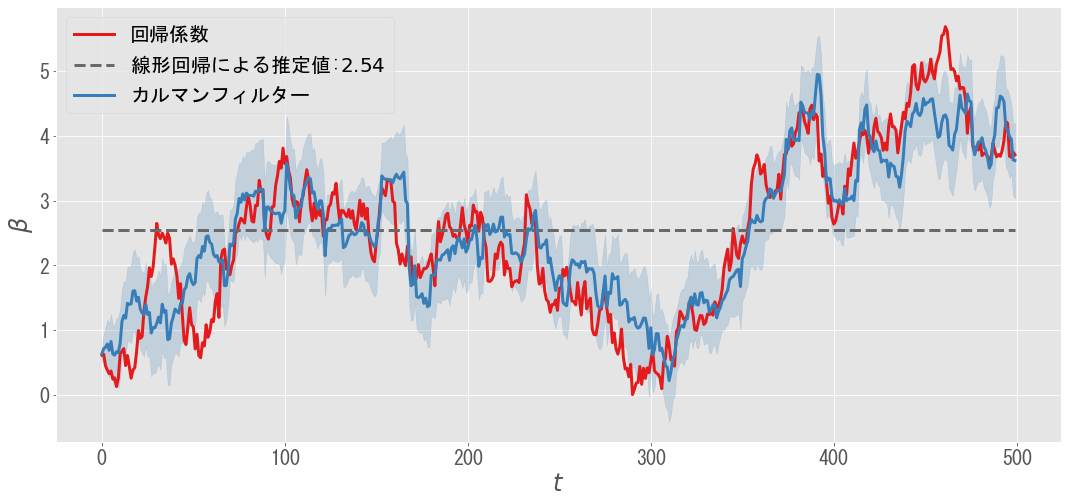
このサンプルデータに対して，（EMアルゴリズムで最適化したパラメータをもとに）カルマンフィルターを適用したものが下図です．カルマンフィルターは，回帰係数$\beta _ t$の時間変化をうまく推定できています．また事後分布$ p({\boldsymbol \beta}_t | {\bf y}_1, \ldots, {\bf y}_t, {\boldsymbol \theta})$をもとに，標準偏差を推定できることもカルマンフィルターの大きな利点の一つです．

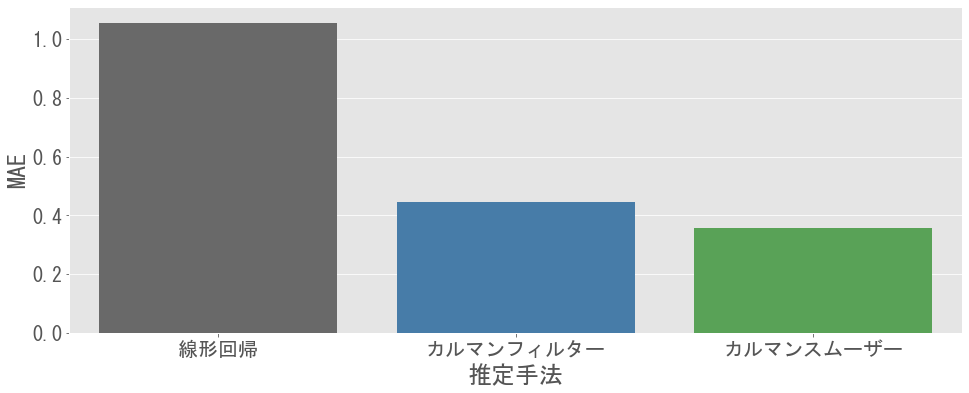
以下のグラフでは，各手法による回帰係数$\beta _ t$の推定精度を平均絶対誤差(MAE)で評価しています（カルマンスムーザーの結果も追加）．カルマンフィルター（とカルマンスムーザー）は線形回帰よりMAEが小さく，より適切なモデルであると考えられます．

限界消費性向の推定

実際のデータに対しても，カルマンフィルターを適用してみます．ここでは，可処分所得と家計最終消費支出のデータをもとに，限界消費性向（所得増加に対する消費支出の感応度）を推定します．データは内閣府が公表する家計可処分所得・家計貯蓄率四半期別速報（参考系列）を使用します．
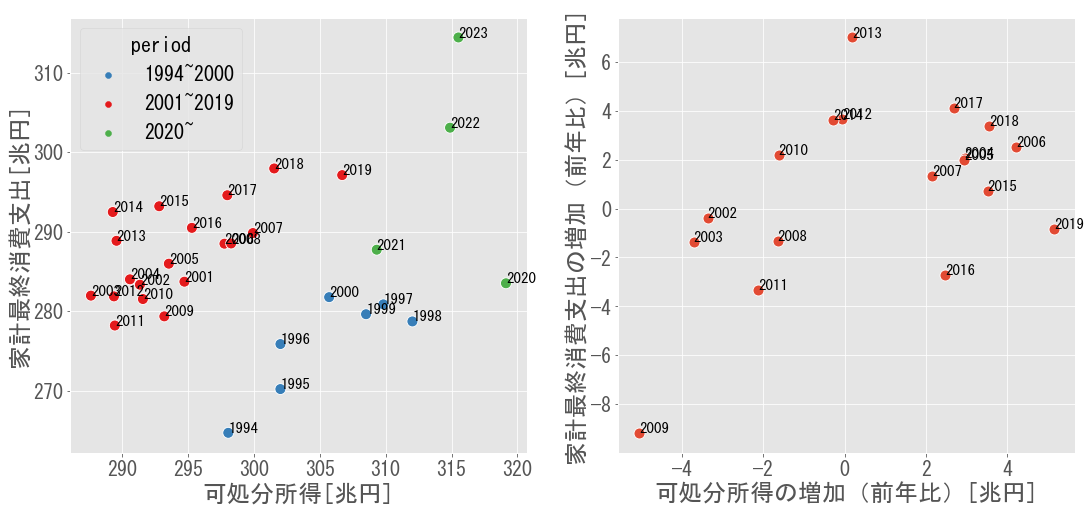
まず可処分所得と家計最終消費支出をそのままプロットした左図を見ると，データは以下の3つの時期に分けられると推察できます．

• 1994~2000年：デフレ進行前であり，可処分所得が増加傾向
• 2001~2019年：デフレ進行後であり，可処分所得が低迷
• 2020年~：コロナショックによる消費支出の低下とその後の回復

ここでは，2001~2019年のデータを対象に分析します．まずトレンドを除去するため，縦軸と横軸を前年比での増加に直したものが右図です．特に2009年のデータを見ると，リーマンショックによる可処分所得と消費支出の減少が確認されます．

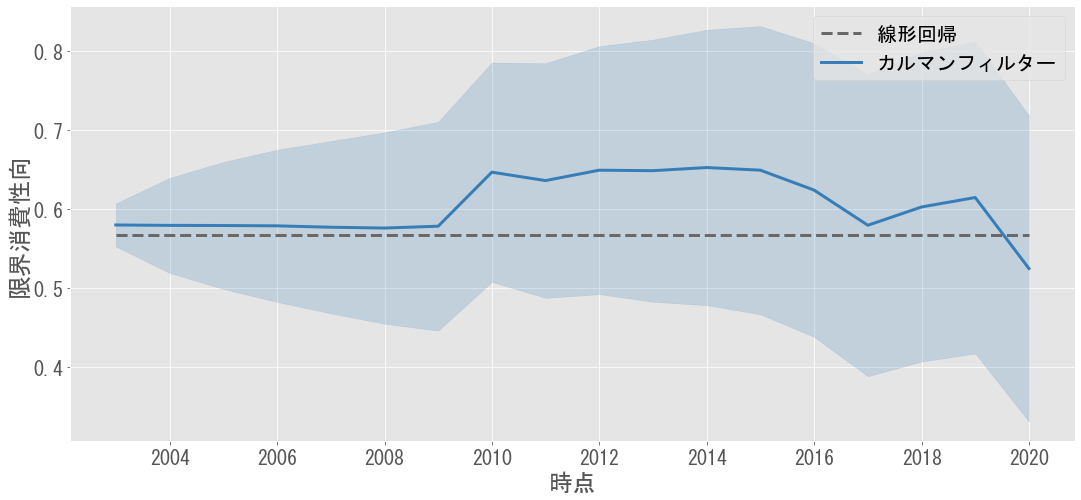
以下のグラフでは，このデータに対して線形回帰とカルマンフィルターを適用し限界消費性向を推定しています．特徴的なのは，リーマンショック（2009年）付近で限界消費性向が上昇している点です．

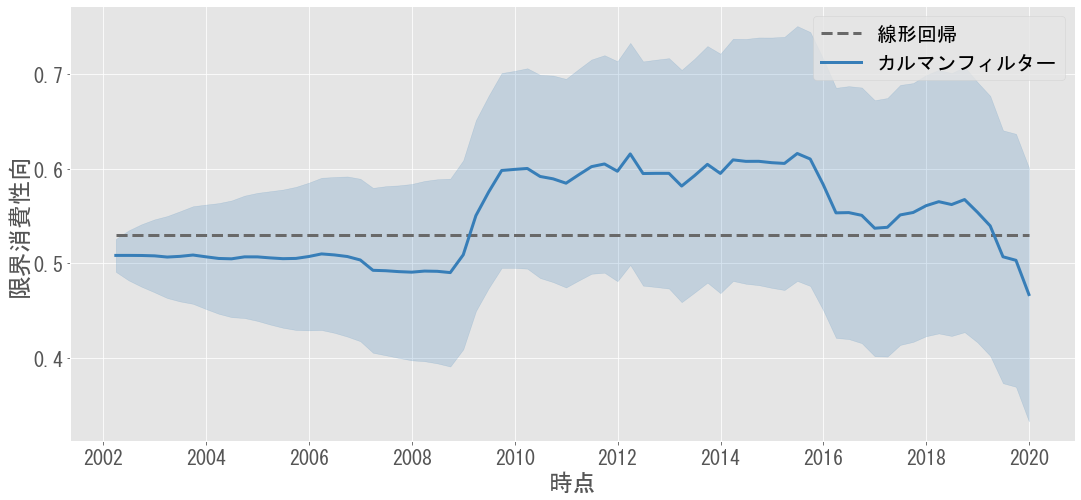
サンプル数を増やすため，四半期のデータ（季節調整済み）で同様の分析をしたものが下図です．こちらでも同様に，リーマンショック以降の限界消費性向の上昇が確認できます．

この結果に対しては「リーマンショック時の不況において，支出を抑える傾向が強まり，可処分所得の減少に伴う消費支出の減少がより強く表れた（感応度が高まった）」と解釈できます．ただし，より精緻な分析のためにはインフレ率の調整等も必要になるでしょう．

まとめと補足

本記事では時間変化する回帰係数をカルマンフィルターによって推定する方法を示しました．実際には，カルマンフィルター（より一般には状態空間モデル）はより広い応用が考えられます．例えば説明変数$X_t$を単位行列とすると，観測値${\bf y} _ t$からノイズを除去して状態変数${\boldsymbol \beta}_t$を推定することになります．また時刻$t$までのデータから時刻$t+1$の状態変数${\boldsymbol \beta} _ {t + 1}$を予測することもできます．
なおカルマンフィルターではノイズが正規分布に従うことを仮定しますが，粒子フィルターを適用する場合にはより幅広い確率分布を扱うことができます．経済データは正規分布に従わないことが多いため，粒子フィルターの適用が適していると考えられます．

参考文献

「経済・ファイナンスのためのカルマンフィルター入門」はカルマンフィルターについてわかりやすく解説した本で，応用例も幅広く紹介されています．

限界消費性向の推定にカルマンフィルターを適用している例としては「平成22年度　年次経済財政報告のコラム2－1図　限界消費性向の推計」が見つかりました．

また金融庁の以下論文では，ベータの推定にカルマンフィルターを適用しており参考となりました．

ディスクレイマー
本記事は筆者の個人的なメモであり，情報の正確性，信頼性，完全性は保証されず，本情報に基づいて被ったいかなる損害についても，一切の責任を負いかねます．

1. PRML 第13章（13.18から13.34まで）解答例では，カルマンフィルターの導出（特にEMアルゴリズム）について丁寧に解説されています（ただしノーテーションおよび切片項の取り扱いが異なる点に注意）．またEMアルゴリズムの数式を追うのは非常に大変です． ↩