金融界隈(?)で少し前に話題になった,Trader-Company法を簡単に実装してみました.ざっくりいうと,Companyが何人かのTraderを抱えており,各Traderの予測に基づいて株式市場の予測を行うというモデルです.
この記事では,非常に単純なダイナミクスを持つ系に話を絞り,実際にTrader-Company法を実装します.ある程度単純化された実装ではありますが,実際にダイナミクスを良い精度で予測できていることを示します.記事全体の実装を示したJupyter Notebookをgithubにアップしています(https://github.com/yotapoon/Trader-Company) .
なお,著者の伊藤さんによる解説記事(https://tech.preferred.jp/ja/blog/trader-company/) と元論文(https://arxiv.org/abs/2012.10215) はこちらです.また,何か論文について誤解している部分などがあればぜひご指摘いただきたく思います.
1 Trader-Company法とは
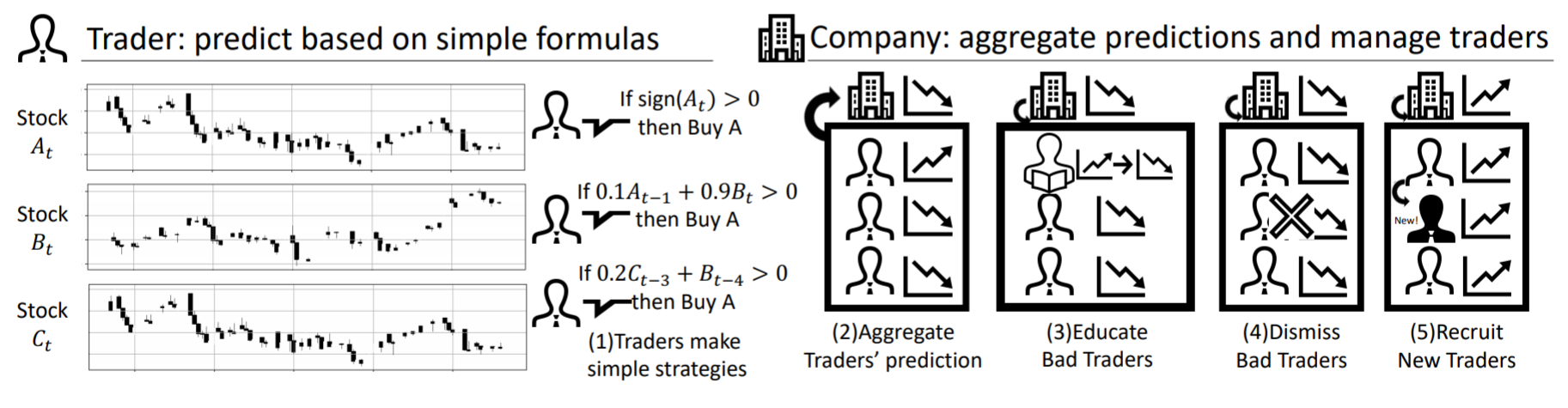
Trader-Company法とは,シンプルな式で将来の株価変動を予測するTraderたちを,Companyが管理するという方法です.これを図にまとめると以下のようになります(元論文から引用).
アルゴリズムとしては,
(1) Traderたちが単純な式に基づき,次の時刻における銘柄$i$の収益率$r_i(t+1)$について予測を行う.この"単純な式"をformula,formulaの各項をfactorと呼ぶ.
(2) (1)における予測をCompanyは集約し,各銘柄に対して予測を行う.
(3) (2)のプロセスにおいて,成績の悪い(つまり予測の下手な)Traderに対してeducationを行う.具体的には,formulaにおけるfactorの各係数$w_j$を最小二乗法により最適化するというプロセスを踏む.
(4) (3)のeducationによっても成績が上がらなかったTraderは解雇されることになる😭(fire).これは,良い予測につながりえないfactorを削除するためである.
(5) 先ほど解雇されたTraderの代わりに,新しいTraderを見つける(recruit).このプロセスにより,精度改善につながるfactorを発見できる可能性がある.
という感じです.
以下では,各々のプロセスについてより詳しく見ていきます.
1.1 Trader
時刻$t$における株式$i$の価格を$X_i[t]$とします.いま
$$
r_i[t] = \log \dfrac{X_i[t]}{X_i[t-1]}
$$
を,時刻$t$における株式$i$の一期先のリターンとして定義します.実際,$X_i[t] > X_i[t-1]$ならばリターンはプラス,そうでなければマイナスです.
いま,注目する銘柄の総数を$S$としましょう.考えたいのは,時刻$0$から$t$の全銘柄のリターンの情報$r_{1:S}[0:t-1]$に基づいて,一期先のリターン$\hat{r} _ {1:S} [t]$を予測するという問題です.ただし,$1:S$や$0:t-1$という記法は,その区間における値をすべて並べたものと考えてください(Pythonを思い浮かべればわかりやすいでしょう,ただし端点を含むことに注意).
そこで,各Traderたちは
$$
f_\Theta (r_{1:S}[0:t-1]) = \sum_{j=1}^M w_j \color{red}{A_j}(\color{blue}{O_j}(r_{P_j}[t-D_j], r_{Q_j}[t-F_j]))
$$
という公式(formula)に基づいて一期先のリターンを予測することになります.各"パラメータ"を以下にまとめました.
| パラメータ | 意味 | 例 |
|---|---|---|
| $M$ | factorの数 | |
| $w_j$ | 各factorの係数 | |
| $\color{red}{A_j}(x)$ | 活性化関数 | $ x, \tanh(x), {\rm sign}(x), {\rm ReLU}(x)$など |
| $\color{blue}{O_j}(x,y)$ | 二項演算子 | $x+y, x> y, xy, x, y, \max(x,y)$など |
| $P_j, Q_j$ | 予測に使う銘柄のインデックス | |
| $D_j,F_j$ | 時間遅れを表すパラメータ |
これだけ見るとどこが"シンプル"なのか分からないかもしれないので,具体例を示します:
$$
\hat{r} _ 0 [t] = 4.92\color{red}{\rm ReLU}(r_1 [t-3]) + 5.86 \color{red}{\rm sign}(\color{blue}{\max}(r_2[t-2], r_3[t-5]))
$$
具体例を見ると,たった二つ(あるいは一つ)の銘柄によってfactorを計算し,それらを重みづけて足し合わせることで予測をしていることがわかります.
いま,表記を簡単にするためにファクターを表す$x_1[t], \cdots, x_M[t]$を導入します.ただし$x_j[t]$は「時刻$t$の"リターン"を予測するための$j$番目のファクター」という意味であり,時刻$t$における量から計算されるわけではないことに注意してください.時刻$t$のリターン$r[t]$の予測$\hat{r}[t]$は
$$
\hat{r} [t] = \sum_{j=1}^M w_j x_j[t] \
$$
となりますが,最小二乗法により$w_j$は
$$
{\bf w} = (X^t X)^{-1} X^t {\bf r}
$$
と求められます.ただし${\bf w} = (w_1, \cdots, w_M)$,${\bf r} = (r[1], \cdots, r[T])$,$X_{tj} = x_j[t]$としています.この手続きをlearnと呼ぶことにします.
一方で,その他の離散的な"パラメータ"をどのように最適化するかは自明でなく,本質的に重要となります.その最適化方法を与えるのがCompanyというクラスです.
一度,Traderの実装を示します.未定義語が多いかもしれませんが,雰囲気をつかんでもらえれば大丈夫です.
time_window = 60
delay_max = 3
class Trader:
def __init__(self, num_factors_max = 4, delay_max = 3): # num_factor_maxはformulaに含まれる項の最大値,delay_maxはどれだけ過去のデータを用いることができるか
self.num_factors_max = num_factors_max
self.delay_max = delay_max
self.num_factors = [[] for _ in range(num_stock)] # Traderは予測したい都市(target)ごとに異なる式を用いるため,targetごとに項の数も異なる.
self.delay_x = [[] for _ in range(num_stock)]
self.delay_y = [[] for _ in range(num_stock)]
self.stock1 = [[] for _ in range(num_stock)]
self.stock2 = [[] for _ in range(num_stock)]
self.w = [[] for _ in range(num_stock)]
self.activation = [[] for _ in range(num_stock)]
self.binary_operator = [[] for _ in range(num_stock)]
self.X_factor = [[] for _ in range(num_stock)]
self.cumulative_error = [[] for _ in range(num_stock)]
for target in range(num_stock):
self.num_factors[target] = np.random.choice(range(1, self.num_factors_max+1))
self.delay_x[target] = np.random.choice(delay_max, self.num_factors[target])
self.delay_y[target] = np.random.choice(delay_max, self.num_factors[target])
self.stock1[target] = [np.random.choice(num_stock) for _ in range(self.num_factors[target])]
self.stock2[target] = [np.random.choice(num_stock) for _ in range(self.num_factors[target])]
self.activation[target] = [np.random.choice(name_activation) for _ in range(self.num_factors[target])]
self.binary_operator[target] = np.random.choice(name_binary_operator, self.num_factors[target])
self.w[target] = np.random.randn(self.num_factors[target])
self.X_factor[target] = np.zeros((0, self.num_factors[target]))
self.cumulative_error[target] = 0.0
def reset_parameters(self, target): # ファクターの行列Xがランク落ちした際に必要
self.num_factors[target] = np.random.choice(range(1, self.num_factors_max+1))
self.delay_x[target] = np.random.choice(delay_max, self.num_factors[target])
self.delay_y[target] = np.random.choice(delay_max, self.num_factors[target])
self.stock1[target] = [np.random.choice(num_stock) for _ in range(self.num_factors[target])]
self.stock2[target] = [np.random.choice(num_stock) for _ in range(self.num_factors[target])]
self.activation[target] = [np.random.choice(name_activation) for _ in range(self.num_factors[target])]
self.binary_operator[target] = np.random.choice(name_binary_operator, self.num_factors[target])
self.w[target] = np.random.randn(self.num_factors[target])
self.X_factor[target] = np.zeros((0, self.num_factors[target]))
self.cumulative_error[target] = 0.0
def calc_factor(self, target, j, data): # traderが持つ,targetに対するj番目のファクターを計算
A = activation[self.activation[target][j]] # 可読性のため代入,以下同様
O = binary_operator[self.binary_operator[target][j]]
P = self.stock1[target][j]
Q = self.stock2[target][j]
D = self.delay_x[target][j]
F = self.delay_y[target][j]
return A(O(data[P][self.delay_max-D], data[Q][self.delay_max-F])) # 論文の式と対応している形
def stack_factors(self, data_to_stack, target): # Companyのメソッドeducationのために必要なデータをstackしておく
factors = np.zeros(self.num_factors[target])
for j in range(self.num_factors[target]): # 各ファクターごとに
factors[j] = self.calc_factor(target, j, data_to_stack)
if len(self.X_factor[target]) < time_window: # time_windowよりもデータがたまっていないときは,ただ下に積むだけ.
self.X_factor[target] = np.vstack([self.X_factor[target], factors])
else: # time_windowよりもデータがたまっているときは,下に積みつつ過去のデータを消してしまう.
self.X_factor[target] = np.roll(self.X_factor[target], -1, axis = 0)
self.X_factor[target][-1] = factors
# y = (y_{t-w-1}, , y_t)
def learn(self, target, y): # 最小二乗法により,各ファクターの係数を最適化する.X_factorを使っていることに注意.
epsilon = 0.0001 # singular matrixが生じないための工夫
X = self.X_factor[target]
if np.linalg.matrix_rank(X.T.dot(X) + epsilon) < self.num_factors[target]:
#print("Note: rank(X_factor) < num_factors.")
self.w[target] = np.zeros(len(self.w[target]))
else:
self.w[target] = np.linalg.inv(X.T.dot(X)+epsilon).dot(X.T).dot(y) # 最小二乗法で係数を求めている
# prediction.shape = (num_stock, time_window)
def predict_for_train(self): # train dataに対するprediction, これに基づいてcumulative_errorを計算し,bad_traderを解雇する.
prediction = np.zeros((num_stock, time_window)) # 過去のデータに対して行うため,prediction.shape = (num_stock, time_window)
for target in range(num_stock):
prediction[target] = self.X_factor[target].dot(self.w[target])
return prediction
def predict_for_test(self): # test dataに対するprediction, これに基づいてモデルの評価を行う.
prediction = np.zeros(num_stock) # 各時刻に対して行うため,prediction.shape (num_stock)
for target in range(num_stock):
prediction[target] = self.X_factor[target][-1].dot(self.w[target])
return prediction
def calc_cumulative_error(self, y_true): # 過去のデータに対してcumulative_errorを計算,これに基づいてbad_traderを見つける.
prediction = self.predict_for_train() # prediction.shape = (num_stock, time_window)
errors = (prediction - y_true)**2.0
errors = np.sqrt(errors.mean(1)) # errorsを時間軸方向について平均
for target in range(num_stock):
self.cumulative_error[target] = errors[target]
ただし,stack_factorsというメソッドは各時刻のfactor $x_1[t], \cdots, x_M[t]$を計算し記録するというものです.
また,外部に辞書型のactivationを用意しており,これに適切な活性化関数名を入れることによりその関数が使えるという仕組みにしています.もっとスマートな方法があれば教えてもらえたらうれしいです.
1.2 Company
前述のTraderをまとめ,パラメータを最適化するのがCompanyです.主なメソッドとしては,aggregate,educate,fire_and_recruitがあります.
aggregate
まず,Companyとしての予測を行うために,Traderたちの予測をまとめ上げる必要があります.これを実行するのがaggregateです.様々な方法が考えられると思いますが,ここでは簡単のために「これまでの累積誤差が少ないTraderを上位$Q$パーセンタイル取り出し,累積誤差の逆数で重みづけ平均をとる」という方法を取りました.まぁ要するに,成績が良いトレーダーを贔屓しつつ予測をするという方法です.
educate
良い予測を行うためには,各トレーダーの予測精度を向上させる必要があります.educateでは,前述のlearnメソッドによる各トレーダーのfactor係数${\bf w}$の最適化を行います.元論文では,成績の悪いTraderに対してのみ実行していましたが,簡単のために全員に対して実行しました.
なお,この逆行列の計算のためには各$t$ごとにファクター$x_j[t]$を記録しておく必要があります(stack_factors).
fire_and_recruit
先ほどのeducateは,連続的なパラメータ$w_j$を最適化するだけでした.離散的な他のパラメータを最適化するには,このメソッドを使う必要があります.
まず,これまでの累積誤差を計算し,成績の上位$Q$パーセンタイルを生き残らせます.そしてその基準に達しなかったTraderたちは残酷にも解雇されてしまい😭,代わりに新しいTraderを生成します.
元論文では混合ガウス分布を使っていましたが,あまり自然に思えなかったので(そして面倒だったので)一様分布から取ってくることにしました.ただし,あるTraderのfactorにまったく同じ意味を持つものが生じてしまうと,educateで述べた$X$がランク落ちしてしまうため,うまく動かないことに注意します.特にこのモデルではわりとそのようなことが起きやすいので,気を付ける必要があります.うまくやればそのような事態が生じないようにパラメータを選べるのかもしれませんが,面倒だったのでランク落ちが生じるたびにパラメータを選び直させるという力業で実装しています.
以下に実装を示します.
class Company:
def __init__(self, num_traders, Q = 0.5): # time_window shold be larger than num_factors_max
self.Q = Q # 1-Qがbad_tradersの割合を表す,つまりQが大きいほど解雇される割合が少なくなる.Qは生存率ともいえる.
self.traders = [[] for _ in range(num_traders)]
for n in range(num_traders):
self.traders[n] = Trader() # 適当にtraderを生成すると同じ意味を持つファクターを持つ可能性があるため,ランク落ちの問題が生じる.
for target in range(num_stock): # 以下の手続きでランク落ちを回避
self.generate_trader_without_singular(n, target, len(y[0]), y) # yがグローバル変数になってるけど許して
self.num_traders = num_traders
self.bad_traders = np.ones((num_stock, num_traders)) > 0.0 # とりあえず全員をbad_traderにしてみた,意味はない
def educate(self, t): # 簡単のために,全トレーダーがeducateされるものとする(論文とは異なることに注意)
for n in range(self.num_traders):
for target in range(num_stock):
y_true = y[target][t-time_window+1:t+1]
self.traders[n].learn(target, y_true) # 最小二乗法により学習を行う.学習に必要なinputはstack_factorsで行っている.
def find_bad_traders(self, y_true): # 過去のデータに基づいてself.bad_tradersを更新する,trainの最中にしか実行されないことに注意.
cumulative_errors = np.zeros((num_stock, self.num_traders))
for n in range(self.num_traders): # 各traderに対して
for target in range(num_stock): # 各銘柄に対して
self.traders[n].calc_cumulative_error(y_true) # cumulative_errorsを計算
cumulative_errors[target][n] = self.traders[n].cumulative_error[target] # bad_tradersをQ-percentileを使って探すために必要
for target in range(num_stock): # 各銘柄について,bad_tradersをQ-percentileを使って探す.
self.bad_traders[target] = cumulative_errors[target] > np.percentile(cumulative_errors[target], 100.0*self.Q)
def fire_and_recruit(self, t, y): # yは時刻tまでのデータ
y_true = y[:,t-time_window+1:t+1]
self.find_bad_traders(y_true) # self.bad_tradersのリストを更新
for n in range(self.num_traders):
for target in range(num_stock):
if self.bad_traders[target][n]:
self.generate_trader_without_singular(n, target, t, y) # ランク落ちを回避しつつ生成,同時にX_factorも計算している
self.traders[n].calc_cumulative_error(y_true) # 次回のfind_bad_tradersのために,累積誤差を計算
def generate_trader_without_singular(self, n, target, t, y): # ランク落ちを回避しつつ新しいTraderを生成
self.traders[n] = Trader()
for target in range(num_stock):
for idx in reversed(range(time_window)):
self.traders[n].stack_factors(y[:,t-delay_max-1-idx:t-idx], target) # X_factorを計算
while np.linalg.matrix_rank(self.traders[n].X_factor[target].T.dot(self.traders[n].X_factor[target])) < self.traders[n].num_factors[target]:
self.traders[n].reset_parameters(target) # rank落ちが発生していたらやり直し
for idx in reversed(range(time_window)):
self.traders[n].stack_factors(y[:,t-delay_max-1-idx:t-idx], target)
def aggregate(self): # Traderたちの意見を集める
predictions = np.zeros((num_stock, self.num_traders))
weights = np.zeros((num_stock, self.num_traders)) # Traderの意見を重みづけする
for n in range(self.num_traders):
for target in range(num_stock):
if not self.bad_traders[target][n]: # Q-パーセンタイル以上の成績の良いTraderのみを対象
weights[target][n] = (1.0 / self.traders[n].cumulative_error[target]) # 重みは累積誤差の逆数,つまり誤差が少ないTraderほど重く見られる
predictions[target][n] = self.traders[n].predict_for_test()[target]
predictions_weighted = np.zeros(num_stock)
for target in range(num_stock):
predictions_weighted[target] = (weights[target]*predictions[target]).sum() / (weights[target].sum())
return predictions_weighted
def observe(self, data_to_stack): # それ以前のデータを観測し,現時点のデータを予測するために利用する.
for n in range(self.num_traders):
for target in range(num_stock):
self.traders[n].stack_factors(data_to_stack, target)
1.3 問題設定と大まかな流れ
全体像を把握したうえで,細かい問題設定を詰め直します.
問題設定
まずデータの前半を訓練データ,後半をテストデータに分けます.そして,訓練データを扱っている間はeducationやfire_and_recruitを行い,パラメータの最適化を続けます.テストデータに移ると,これらを行わず,パラメータを固定して予測を行います.
さらに現実的な設定のために,使えるデータに制約を加えます.具体的には,現時点からtime_windowだけ前のデータのみを使いeducationやfire_and_recruitを行います.元論文ではさらに,予測からその取引執行までに遅れがあるという制約まで設けていますが,ここでは簡単のために省略しています.
アルゴリズムの全体
全体としてのアルゴリズムは以下のようになっています.
from tqdm import tqdm # プログレスバーを表示するため
model = Company(20)
errors_test = []
num_test_data = 400 # test dataのサイズ
T = T_total - num_test_data # train dataのサイズ
for t in tqdm(range(delay_max+1, len(y[0]))):
data_to_stack = y[:,t-delay_max-1:t] # t-1までのデータであることに注意
model.observe(data_to_stack) # train, testいずれの場合でもstackしなければならない
# train or test
if delay_max + 1 + time_window < t <= T: # train
model.educate(t)
model.fire_and_recruit(t, y)
elif T < t: # test
prediction_test = model.aggregate()
errors_test.append(np.abs(y[:,t] - prediction_test))
2 今回の実験
前述の実装が正しいかを確認するために,トイモデルに対してきちんと動くかを確かめました.その結果,ある程度の精度をもって正しく予測ができていることが示されました.
2.1 データと比較手法
非常に簡単に,データは$2$つの銘柄に絞ります.また,それぞれの銘柄の収益率$y_0(t), y_1(t)$は以下のようなダイナミクスに従うこととします
y_0[t+1] = \tanh(y_0[t]) + 0.8 y_0[t] y_t[1] - {\rm ReLU} (\min(y_0[t], y_1[t])) + \epsilon_0[t] \\
y_1[t+1] = 0.6 {\rm sign}(y_1[t]) + 0.5 y_0[t]y_t[1] -1.0 \max(y_0[t], y_1[t]) + \epsilon_1[t]
ただし$\epsilon_0[t], \epsilon_1[t]$は分散$\sigma^2$の正規分布に従う独立な乱数(ノイズ)とします.あくまでトイモデルなので,Traderがうまく動いてくれれば,良い予測ができるようなダイナミクスになっています.
このダイナミクスから,
\hat{y}_0[t+1] = \tanh(y_0[t]) + 0.8 y_0[t] y_t[1] - {\rm ReLU} (\min(y_0[t], y_1[t]))\\
\hat{y}_1[t+1] = 0.6 {\rm sign}(y_1[t]) + 0.5 y_0[t]y_t[1] -1.0 \max(y_0[t], y_1[t])
のような予測$\hat{y} _ {0} (t+1)$,$\hat{y} _ {1} (t+1)$を行うことで最も精度が良くなることが直ちにわかります.
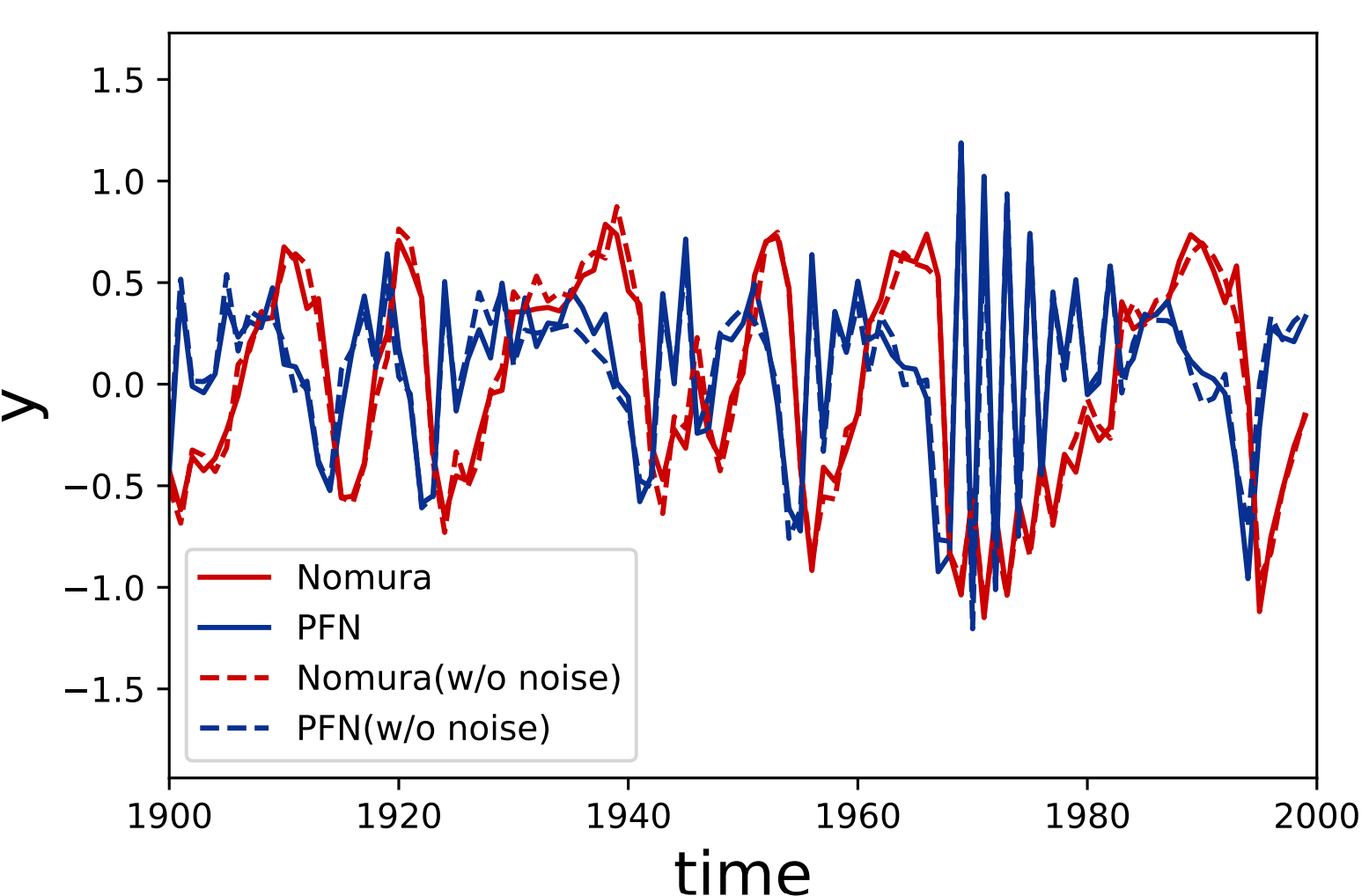
仮にNomura,PFNという二銘柄のダイナミクスが上式に従うものとして,十分時間が経過したときのふるまいを示したものが下図です.ただし,ノイズがない式に基づく予測$\hat{y} _ {0} (t+1)$,$\hat{y} _ {1} (t+1)$を点線で示しました.いい感じで不規則でありつつ,完全にランダムというわけでもない時系列が得られています(実はこんなダイナミクスを得るのが非常に難しかった).
これらの時系列を,Trader-Company法によって予測することを目標とします.比較対象としては,各時刻において何も予測しない(つまり$\hat{y} _ {0} (t+1)=0$,$\hat{y} _ {1} (t+1)=0$とした)場合とVector Autoregression (VAR)の二つの手法を用いました.
2.2 結果
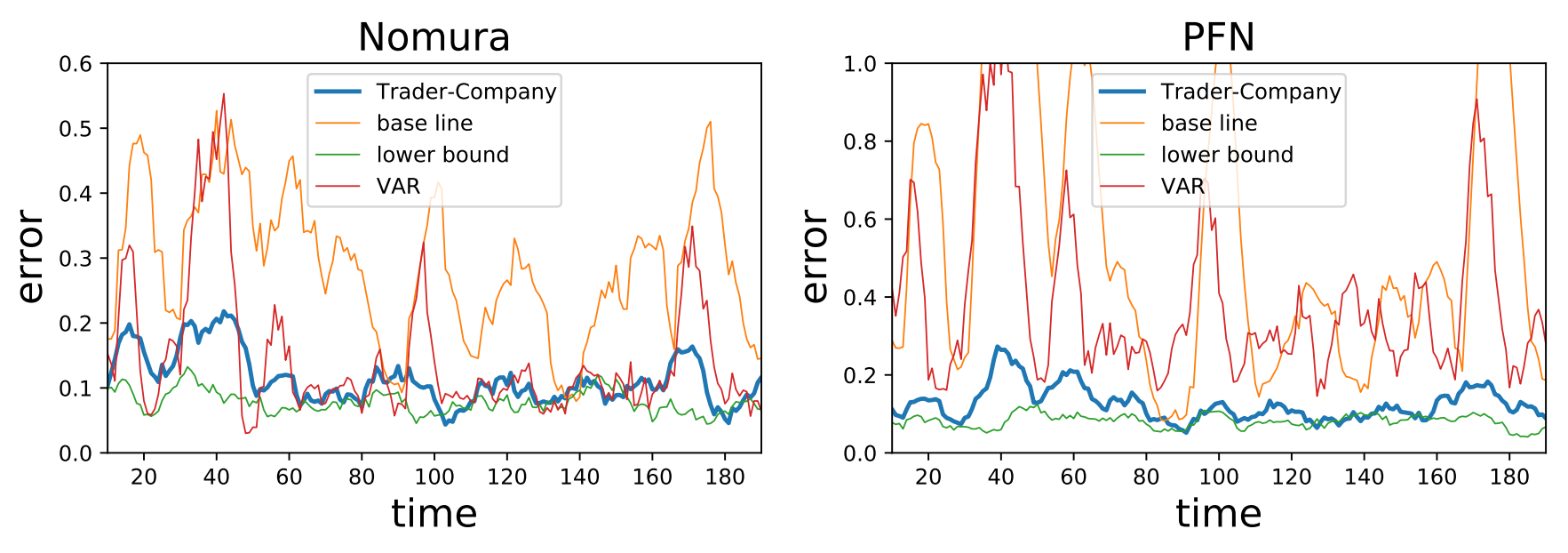
以下の図は,テストフェーズでのエラーを示しています.また,見やすいように適当に平滑化を行っています.ベースライン(何も予測をしない場合)やVARと比較すると,非常に良い精度で予測ができていることに注意します.最適化しやすいようなダイナミクスを選んではいますが,きちんと動いていることの確認には十分な結果が得られました.
各手法ごとに,各銘柄に対するテストエラーの時間平均をとったものが以下の表です.Trader-Company法がベースラインやVARを上回るパフォーマンスを示していることが確認できます.
| 手法 | Nomura | PFN |
|---|---|---|
| ベースライン | 0.2840 | 0.5831 |
| VAR | 0.1426 | 0.3812 |
| Trader-Company | 0.1143 | 0.1245 |
| 最適な予測 | 0.0783 | 0.0814 |
また,各銘柄に対して最適なパフォーマンスを示した(つまり累積誤差が最も小さかった)トレーダーの持つファクターを以下の表に示しました.割とあっているような感じはありますが,完全に一致しているというわけでもないようです.ある程度当たっているファクターがあれば,その他のファクターは他のトレーダーの持つファクターと打ち消しあうという感じなのでしょうか.ここは検証が必要かもしれません.
| Nomura | PFN | |
|---|---|---|
| ファクター1 | $\tanh(xy)$ | $\max(x,y)$ |
| ファクター2 | $x$ | ${\rm sign}(\min(x,y))$ |
| ファクター3 | ${\rm ReLU}(xy)$ | ${\rm sign}(x)$ |
| ファクター4 | $x$ | ${\rm sign}(\max(x,y))$ |
3 まとめ
Trader-Company法の概要と実装を示し,実際に簡単なデータに対して正しく動作しているかを確かめました.その結果,他の手法と比較してもよい精度が得られていることがわかりました.
ただ,この記事ではあくまで実データへの応用は行っていないので,何らかのデータに対してこの手法を用いることができるかを考える必要があります.また,実装を簡単にするためにいくつか簡略化している部分もあるので,そこを改善することも必要になります.