#ローカルから「google colaboratory」にcsvをインストール
今回は、セントラルリーグの現時点で１軍登録されてから、通算で規定打席以上に到達した野手を主に、重回帰分析をして年俸予測した。
Excelにまとめた選手の通算成績を独自に集計したcsvファイルを読み込む。
出典元:BASEBALL LAB、NPB公式ホームページ
Salary_Central_ATBATcsv.ipynb
from google.colab import files
uploaded = files.upload()
#インストール結果を表示
data.head()で最大５つまで表示できるが、ここでは贔屓の中日京田選手にのみとする。
Salary_Central_ATBATcsv.ipynb
import pandas as pd
import io
data = pd.read_csv(io.StringIO(uploaded['Central_ATBAT1.csv'].decode('utf-8')), header=None)
data.head()
インストール結果の説明をします。既製の成績だけでは、差別化ができないので、今回はセイバーメトリクスを採用する。
各選手の生涯成績から独自に算出した指標を４つ紹介する。
出典：ウィキペディア
| セイバーメトリクスとは | |
|---|---|
| 指標 | 説明 |
| wOBA | wOBAは打者が1打席あたりにどれだけチームの得点増加に貢献したかを表す指標である。 平均的な数字は、0.330 wOBA (NPB) = {0.69×（四球－敬遠）＋0.73×死球＋0.92×失策出塁＋0.87×単打＋1.29×二塁打＋1.74×三塁打＋2.07×本塁打}÷(打数 + 四球 – 敬遠 + 犠飛 + 死球) |
| wRAA | wRAA (Weighted Runs Above Average) はwOBAを用いて打者の打撃貢献度を測る指標である。平均的な打者が同じ打席数立った場合に比べて増やした得点を示している。総合指標のWARではwRAAをベースに打撃の貢献度を算出している。 wRAA = (対象打者のwOBA - リーグwOBA) ÷ wOBAscale × 打席数 |
| wRC | wRC (Weighted Runs Created) はwOBAをベースに打者が産み出した得点を測る指標である。リーグ平均に対する得点の増減を測るwRAAとリーグの平均的な得点力を足し合わせた形をしている。 wRC = wRAA + (リーグ総得点数 / リーグ総打席数) × 打席数 |
| wRC+ | wRC+ (Weighted Runs Created Plus) は打者が打席あたりに産み出した得点の傑出度であり、平均的な打者に対する得点力の大きさをパーセンテージで表している。wRC+が100の打者は平均的であり、wRC+が150の打者は平均より50%多くの得点を産み出している。リーグごとの得点環境やパークファクターも考慮されているため、リーグや時代を問わず一律の条件で打者を比較評価する事が出来る。打席あたりのwRCをリーグの平均的な得点力で割った形をしている。 wRC+= { (パークファクター補正を加えたwRAA / 打席数) ÷ (リーグ総得点数 / リーグ総打席数) + 1 } × 100=(パークファクター補正を加えたwRC / 打席数)÷(リーグ総得点数 / リーグ総打席数)×100 |
| 選手 | 京田 陽太 |
|---|---|
| 球団 | 中 |
| wOBA | 0.35152 |
| wRAA | 10.44774 |
| wRC | 77.2722 |
| wRC+ | 112.664 |
| 試合 | 141 |
| 打席 | 602 |
| 打数 | 564 |
| 得点 | 67 |
| 安打 | 149 |
| 二塁打 | 23 |
| 三塁打 | 8 |
| 本塁打 | 4 |
| 塁打 | 200 |
| 打点 | 36 |
| 三振 | 105 |
| 四球 | 18 |
| 敬遠 | 0 |
| 死球 | 9 |
| 犠打 | 10 |
| 犠飛 | 1 |
| 盗塁 | 23 |
| 盗塁刺 | 13 |
| 併殺打 | 5 |
| 失策 | 14 |
| 打率 | 0.015 |
| 長打率 | 0.024 |
| 出塁率 | 0.015 |
| OPS | 0.039 |
| PF | 0.81 |
| 年俸 百万円 |
40 |
OPS低い！！！
Salary_Central_ATBATcsv.ipynb
df = pd.read_csv("Central_ATBAT.csv") #データの読み込み
#重回帰分析で係数と決定係数を算出
初心者向けに機械学習のオープンソースライブラリ「scikit-learn」を使ってみた。
Salary_Central_ATBATcsv.ipynb
import pandas as pd
import numpy as np
from sklearn import linear_model
from sklearn.externals import joblib
# CSVファイルの読み込み
data = pd.read_csv("Central_ATBAT1.csv", sep=",")
# 回帰モデルの呼び出し
clf = linear_model.LinearRegression()
# 説明変数にデータを使用
X = data.loc[:, ['wOBA', 'wRAA', 'wRC', 'wRC+','試合', '打席', '打数', '得点', '二塁打', '三塁打', '本塁打', '塁打', '打点', '三振', '四球', '敬遠', '死球', '犠打', '犠飛', '盗塁','盗塁刺', '併殺打', '失策', '打率','長打率', '出塁率', 'OPS', 'PF']].values
# 目的変数に使用
Y = data['年俸\n 百万円'].values#目的変数のネーミングはご容赦下さい。
# 予測モデルを作成（重回帰）
clf.fit(X, Y)
# 回帰係数と切片の抽出
a = clf.coef_
b = clf.intercept_
# 回帰係数
print("回帰係数:", a)
print("切片:", b)
print("決定係数:", clf.score(X, Y))
# 学習結果を出力
joblib.dump(clf, 'multiple.learn')
結果
回帰係数: [ 5.85165549e+02 -1.22795112e+01 -2.89334562e+00 -2.31718536e-01
-2.17035948e-01 -7.30060305e+00 3.42709721e+00 4.10296016e-01
3.27715436e+00 -6.91265616e+00 -1.06841983e+01 1.17405127e+01
5.08741941e-02 1.24236328e-01 1.19694240e+01 -5.78366232e+00
2.94385282e+00 7.79098143e+00 3.45047143e+00 3.51341925e+00
-7.40089519e+00 5.33763399e-01 1.09093124e+01 5.46356908e+02
6.72671523e+02 6.79070320e+02 -9.17805174e+02 -9.51199001e+01]
切片: -42.600065929210984
決定係数: 0.7954080767578464
['multiple.learn']
決定係数は１に近いほど良いとされています。せめて0.85には近づけたいものです。
#変数増減法（ステップワイズ法）
決定係数の精度を上げるために、重みαを付けて説明変数を減らしてみる。
α= 0 とした場合、Ridge回帰となる。
Salary_Central_ATBATcsv.ipynb
import pandas as pd
import numpy as np
from sklearn import linear_model
from sklearn.externals import joblib
# CSVファイルの読み込み
data = pd.read_csv("Central_ATBAT1.csv", sep=",")
# 回帰モデルの呼び出し
clf = linear_model.Ridge(alpha=0.0, fit_intercept=True,
normalize=False, copy_X=True,
max_iter=10000, tol=0.0001,random_state=None)
# 説明変数にx1とx2のデータを使用
X = data.loc[:, ['wOBA', 'wRAA', 'wRC', 'wRC+','試合', '打席', '打数', '得点', '二塁打', '三塁打', '本塁打', '塁打', '打点', '三振', '四球', '敬遠', '死球', '犠打', '犠飛', '盗塁','盗塁刺', '併殺打', '失策', '打率','長打率', '出塁率', 'OPS', 'PF']].values
# 目的変数にx3のデータを使用
Y = data['年俸\n 百万円'].values
# 予測モデルを作成（重回帰）
clf.fit(X, Y)
# 回帰係数と切片の抽出
a = clf.coef_
b = clf.intercept_
# 回帰係数
print("回帰係数:", a)
print("切片:", b)
print("決定係数:", clf.score(X, Y))
# 学習結果を出力
joblib.dump(clf, 'multiple.learn')
結果
回帰係数: [ 5.85165548e+02 -1.22795112e+01 -2.89334562e+00 -2.31718534e-01
-2.17035948e-01 -7.30060317e+00 3.42709733e+00 4.10296016e-01
3.27715436e+00 -6.91265616e+00 -1.06841983e+01 1.17405127e+01
5.08741942e-02 1.24236328e-01 1.19694241e+01 -5.78366231e+00
2.94385294e+00 7.79098156e+00 3.45047156e+00 3.51341925e+00
-7.40089519e+00 5.33763399e-01 1.09093124e+01 5.46356909e+02
6.72671525e+02 6.79070321e+02 -9.17805176e+02 -9.51199001e+01]
切片: -42.600065650018166
決定係数: 0.7954080767578481
['multiple.learn']
たいして変わりまへん。
α= 1 とした場合、Lasso回帰ならどーなる？
Salary_Central_ATBATcsv.ipynb
import pandas as pd
import numpy as np
from sklearn import linear_model
from sklearn.externals import joblib
# CSVファイルの読み込み
data = pd.read_csv("Central_ATBAT1.csv", sep=",")
# 回帰モデルの呼び出し
clf = linear_model.Lasso(alpha=1.0, fit_intercept=True,
normalize=False, copy_X=True,
max_iter=10000, tol=0.00001,
warm_start=False, positive=False,
random_state=None, selection="cyclic")
# 説明変数にデータを使用
X = data.loc[:, ['wOBA', 'wRAA', 'wRC', 'wRC+','試合', '打席', '打数', '得点', '二塁打', '三塁打', '本塁打', '塁打', '打点', '三振', '四球', '敬遠', '死球', '犠打', '犠飛', '盗塁','盗塁刺', '併殺打', '失策', '打率','長打率', '出塁率', 'OPS', 'PF']].values
# 目的変数にデータを使用
Y = data['年俸\n 百万円'].values
# 予測モデルを作成（重回帰）
clf.fit(X, Y)
# 回帰係数と切片の抽出
a = clf.coef_
b = clf.intercept_
# 回帰係数
print("回帰係数:", a)
print("切片:", b)
print("決定係数:", clf.score(X, Y))
結果
回帰係数: [ 0. 1.88755457 -2.6433344 0.2650838 -0.1813582 0.09682841
-0.04739067 0.28734258 -0.22215838 -3.49688315 -1.30113741 0.85788655
0.03687723 0.09358743 0.29104208 -2.84061011 -0.32120752 0.01346425
0.3931877 0.64703574 -1.24956932 0.61018707 0.10306231 -0.
-0. -0. -0. -0. ]
切片: 8.28184724902951
決定係数: 0.7530352777573788
切片（せっぺん）が小さくなりましたが、決定係数が下がってしまいました。
なら、0 < α< 1 の場合に、Elastic Net(R - glmnet)であればどーなる？
Salary_Central_ATBATcsv.ipynb
import numpy as np
from sklearn import linear_model
from sklearn.externals import joblib
# CSVファイルの読み込み
data = pd.read_csv("Central_ATBAT1.csv", sep=",")
# 回帰モデルの呼び出し。max_iterはk-meansアルゴリズムの内部の最大イテレーション回数。
clf = linear_model.ElasticNet(alpha=1.0, fit_intercept=True,
normalize=False, copy_X=True,
max_iter=10000, tol=0.0001,
warm_start=False, positive=False,
random_state=None, selection="cyclic")
# 説明変数にx1とx2のデータを使用
X = data.loc[:, ['wOBA', 'wRAA', 'wRC', 'wRC+','試合', '打席', '打数', '得点', '二塁打', '三塁打', '本塁打', '塁打', '打点', '三振', '四球', '敬遠', '死球', '犠打', '犠飛', '盗塁','盗塁刺', '併殺打', '失策', '打率','長打率', '出塁率', 'OPS', 'PF']].values
Y = data['年俸\n 百万円'].values
# 予測モデルを作成（重回帰）
clf.fit(X, Y)
# 回帰係数と切片の抽出
a = clf.coef_
b = clf.intercept_
# 回帰係数
print("回帰係数:", a)
print("切片:", b)
print("決定係数:", clf.score(X, Y))
# 学習結果を出力
joblib.dump(clf, 'multiple.learn')
結果
回帰係数: [ 0. 1.88174845 -2.64761641 0.27316407 -0.18315739 0.10003152
-0.05012409 0.28814083 -0.1922804 -3.28344432 -1.2734569 0.8498251
0.04746135 0.08869073 0.2845043 -2.69691912 -0.33246536 0.0184688
0.35745684 0.66732225 -1.29880638 0.63143745 0.12546219 -0.
-0. -0. -0.24008131 -0.68176555]
切片: 8.037747969302814
決定係数: 0.7530301478122973
決定係数は下がるものの、説明変数は絞ることができる。のちの最小二乗法で活かせるかも。
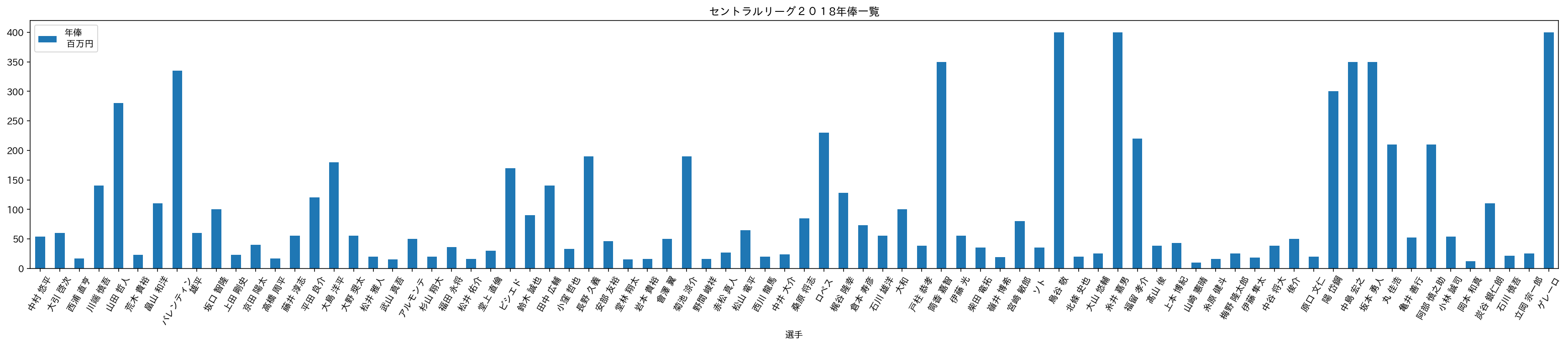
#グラフで可視化
最小二乗法に入る前に、予測と見比べるため推定年俸を可視化する。
Salary_Central_ATBATcsv.ipynb
import pandas as pd
import numpy as np
import japanize_matplotlib
jp_font = {'fontname':'IPAexGothic'}
df = pd.read_csv('Central_ATBAT1.csv')
from matplotlib import pyplot as plt
%config InlineBackend.figure_formats = {'png', 'retina'}
%matplotlib inline
df.plot.bar(x='選手', y='年俸\n 百万円',rot=(60),figsize=(30,5), title='セントラルリーグ２０１8年俸一覧')#y='年俸\n 百万円'こちらもご容赦下さい。
#最小二乗法
いよいよメインディッシュ。肩慣らしはこのぐらいにして、最小二乗法のオープンソースライブラリ「statsmodels」を使って、きめ細かな重回帰分析を実装します。
決定係数だけでなく、補正決定係数に注目します。目安としては、0.500以上あれば良いとされています。
Salary_Central_ATBATcsv.ipynb
mport pandas as pd
import statsmodels.api as sm
df = pd.read_csv('Central_ATBAT1.csv')
x = pd.get_dummies(df[['wOBA', 'wRAA', 'wRC', 'wRC+','試合', '打席', '打数', '得点', '二塁打', '三塁打', '本塁打', '塁打', '打点', '三振', '四球', '敬遠', '死球', '犠打', '犠飛', '盗塁','盗塁刺', '併殺打', '失策', '打率','長打率', '出塁率', 'OPS', 'PF']]) # 説明変数
y = df['年俸\n 百万円'] # 目的変数
# 定数項(y切片)を必要とする線形回帰のモデル式ならば必須
X = sm.add_constant(x)
# 最小二乗法でモデル化
model = sm.OLS(y, X)
result = model.fit()
# 重回帰分析の結果を表示する
result.summary()
結果
| Dep. Variable: | 年俸 百万円 | R-squared: | 0.795 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared: | 0.678 |
| Method: | Least Squares | F-statistic: | 6.804 |
| Date: | Mon, 01 Jul 2019 | Prob (F-statistic): | 3.37E-09 |
| Time: | 12:11:51 | Log-Likelihood: | -413.9 |
| No. Observations: | 78 | AIC: | 885.8 |
| Df Residuals: | 49 | BIC: | 954.1 |
| Df Model: | 28 |
| セイバー各成績 | coef（係数） | std err (標準誤差) | t値 | P値>t値の２乗 | 0.025 | 0.975 |
|---|---|---|---|---|---|---|
| const | -42.6001 | 248.005 | -0.172 | 0.864 | -540.985 | 455.785 |
| wOBA | 585.1655 | 1006.715 | 0.581 | 0.564 | -1437.905 | 2608.236 |
| wRAA | -12.2795 | 5.667 | -2.167 | 0.035 | -23.667 | -0.892 |
| wRC | -2.8933 | 2.041 | -1.418 | 0.163 | -6.995 | 1.208 |
| wRC+ | -0.2317 | 1.373 | -0.169 | 0.867 | -2.991 | 2.528 |
| 試合 | -0.217 | 0.102 | -2.134 | 0.038 | -0.421 | -0.013 |
| 打席 | -7.3006 | 29.047 | -0.251 | 0.803 | -65.673 | 51.072 |
| 打数 | 3.4271 | 29.082 | 0.118 | 0.907 | -55.016 | 61.87 |
| 得点 | 0.4103 | 0.47 | 0.873 | 0.387 | -0.534 | 1.354 |
| 二塁打 | 3.2772 | 1.757 | 1.865 | 0.068 | -0.253 | 6.808 |
| 三塁打 | -6.9127 | 3.465 | -1.995 | 0.052 | -13.875 | 0.05 |
| 本塁打 | -10.6842 | 3.744 | -2.854 | 0.006 | -18.207 | -3.161 |
| 塁打 | 11.7405 | 4.282 | 2.742 | 0.009 | 3.136 | 20.345 |
| 打点 | 0.0509 | 0.563 | 0.09 | 0.928 | -1.081 | 1.182 |
| 三振 | 0.1242 | 0.169 | 0.733 | 0.467 | -0.216 | 0.465 |
| 四球 | 11.9694 | 29.021 | 0.412 | 0.682 | -46.351 | 70.29 |
| 敬遠 | -5.7837 | 3.09 | -1.872 | 0.067 | -11.993 | 0.425 |
| 死球 | 2.9439 | 29.059 | 0.101 | 0.92 | -55.452 | 61.34 |
| 犠打 | 7.791 | 29.032 | 0.268 | 0.79 | -50.551 | 66.133 |
| 犠飛 | 3.4505 | 29.031 | 0.119 | 0.906 | -54.889 | 61.79 |
| 盗塁 | 3.5134 | 1.247 | 2.816 | 0.007 | 1.007 | 6.02 |
| 盗塁刺 | -7.4009 | 2.908 | -2.545 | 0.014 | -13.245 | -1.557 |
| 併殺打 | 0.5338 | 0.977 | 0.546 | 0.587 | -1.43 | 2.497 |
| 失策 | 10.9093 | 4.23 | 2.579 | 0.013 | 2.408 | 19.41 |
| 打率 | 546.3569 | 484.411 | 1.128 | 0.265 | -427.103 | 1519.816 |
| 長打率 | 672.6715 | 1.20E+04 | 0.056 | 0.956 | -2.35E+04 | 2.49E+04 |
| 出塁率 | 679.0703 | 1.20E+04 | 0.057 | 0.955 | -2.34E+04 | 2.48E+04 |
| OPS | -917.8052 | 1.20E+04 | -0.076 | 0.939 | -2.51E+04 | 2.33E+04 |
| PF | -95.1199 | 83.135 | -1.144 | 0.258 | -262.185 | 71.945 |
| Omnibus: | 72.607 | Durbin-Watson: | 1.744 |
|---|---|---|---|
| Prob(Omnibus): | 0 | Jarque-Bera (JB): | 712.66 |
| Skew: | 2.664 | Prob(JB): | 1.77E-155 |
| Kurtosis: | 16.816 | Cond. No. | 1.21E+07 |
| ここでまず注目なのは多重共線性です。これは、説明変数間で非常に強い相関があることを指し、この値が大きいと回帰係数の分散が大きくなり、モデルの予測結果が悪くなることが知られています。 |
この例でいうと、重回帰分析Cond.No. 1.13e+05と非常に大きい数字になっているので、多重共線性の可能性が大いにありえます。
ただし、重回帰分析を行う目的が『因果関係の洞察』ではなく、『予測』であれば、気にしなくて大丈夫です。
次に見るべきは、Prob (F-statistic)F有意性は、3.37e-09なので信頼できる。
#予測と実際の年俸を比べる
Salary_Central_ATBATcsv.ipynb
import matplotlib.pyplot as plt
import japanize_matplotlib
pred = result.predict(X)
df['予測'] = pred
df.plot.bar(y=['年俸\n 百万円','予測'], x='選手',rot=(60),figsize=(60,5), title='Adj. R-squared（修正決定係数）:0.678')
ブルー：推定年俸 オレンジ：予測
#ステップワイズ法ふたたび
説明変数の候補がたくさんあれば、とりあえず全ての説明変数を重回帰分析にかけてp値が小さく、t値の絶対値が大きいものを探索するというやり方をステップワイズ法と言います。
このときのp値は0.05以下ではなく、0.1以下で見ることが慣例のようです。
しかし、ここでは説明変数がほとんどなくなってしまうので、先の変数増減法で出た「ElasticNet」を採用してみます。
まずは、欠損値のチェック。欠損値があれば、正確なデータを分析できないので、チェックしましょう。
Salary_Central_ATBATcsv.ipynb
import pandas as pd
## トレーニングデータとテストデータのCSVファイルをpandasデータフレームとして読み込み
test = pd.read_csv('Central_ATBAT1.csv')
## 概要確認
test.head(181)
## トレーニング、テストデータのデータ数確認
len(test.index)
## 値がnullの項目数を数える
test.isnull().sum()
欠損値はないようです。
選手 0
球団 0
wOBA 0
wRAA 0
wRC 0
wRC+ 0
試合 0
打席 0
打数 0
得点 0
安打 0
二塁打 0
三塁打 0
本塁打 0
塁打 0
打点 0
三振 0
四球 0
敬遠 0
死球 0
犠打 0
犠飛 0
盗塁 0
盗塁刺 0
併殺打 0
失策 0
打率 0
長打率 0
出塁率 0
OPS 0
PF 0
年俸\n 百万円 0
dtype: int64
Ridge回帰とLasso回帰を兼ね備えたElasticNetの説明変数を反映させると修正決定係数は、Adj. R-squared: 0.693に上昇した。
Salary_Central_ATBATcsv.ipynb
import pandas as pd
import statsmodels.api as sm
df = pd.read_csv('Central_ATBAT1.csv')
x = pd.get_dummies(df[['wRAA', 'wRC', 'wRC+','試合', '打席', '打数', '得点', '二塁打', '三塁打', '本塁打', '塁打', '打点', '三振', '四球', '敬遠', '死球', '犠打', '犠飛', '盗塁','盗塁刺', '併殺打', '失策', 'OPS', 'PF']]) # 説明変数
y = df['年俸\n 百万円'] # 目的変数
# 定数項(y切片)を必要とする線形回帰のモデル式ならば必須
X = sm.add_constant(x)
# 最小二乗法でモデル化
model = sm.OLS(y, X)
result = model.fit()
# 重回帰分析の結果を表示する
result.summary()
結果
| Dep. Variable: | 年俸 百万円 | R-squared: | 0.789 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared: | 0.693 |
| Method: | Least Squares | F-statistic: | 8.23E+00 |
| Date: | Mon, 15 Jul 2019 | Prob (F-statistic): | 1.10E-10 |
| Time: | 9:16:49 | Log-Likelihood: | -415.19 |
| No. Observations: | 78 | AIC: | 880.4 |
| Df Residuals: | 53 | BIC: | 939.3 |
| Df Model: | 24 |
| coef （係数） | std err（標準誤差） | t | P>t の２乗 | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| const | 78.4826 | 68.753 | 1.142 | 0.259 | -59.419 | 216.384 |
| wRAA | -11.6742 | 5.407 | -2.159 | 0.035 | -22.519 | -0.829 |
| wRC | -2.8682 | 1.78 | -1.611 | 0.113 | -6.438 | 0.702 |
| wRC+ | 0.4449 | 0.3 | 1.484 | 0.144 | -0.156 | 1.046 |
| 試合 | -0.2223 | 0.098 | -2.263 | 0.028 | -0.419 | -0.025 |
| 打席 | 0.6194 | 25.519 | 0.024 | 0.981 | -50.566 | 51.804 |
| 打数 | -4.3306 | 25.514 | -0.17 | 0.866 | -55.505 | 46.844 |
| 得点 | 0.2999 | 0.448 | 0.669 | 0.506 | -0.599 | 1.198 |
| 二塁打 | 3.1162 | 1.67 | 1.866 | 0.068 | -0.234 | 6.467 |
| 三塁打 | -6.8801 | 3.337 | -2.062 | 0.044 | -13.574 | -0.187 |
| 本塁打 | -10.4578 | 3.514 | -2.976 | 0.004 | -17.506 | -3.41 |
| 塁打 | 11.3204 | 3.987 | 2.839 | 0.006 | 3.323 | 19.318 |
| 打点 | 0.1011 | 0.538 | 0.188 | 0.852 | -0.978 | 1.18 |
| 三振 | 0.1235 | 0.163 | 0.756 | 0.453 | -0.204 | 0.451 |
| 四球 | 3.8802 | 25.589 | 0.152 | 0.88 | -47.444 | 55.204 |
| 敬遠 | -5.8718 | 2.793 | -2.102 | 0.04 | -11.475 | -0.269 |
| 死球 | -4.8162 | 25.456 | -0.189 | 0.851 | -55.875 | 46.242 |
| 犠打 | -0.1036 | 25.517 | -0.004 | 0.997 | -51.284 | 51.077 |
| 犠飛 | -3.9334 | 25.497 | -0.154 | 0.878 | -55.073 | 47.206 |
| 盗塁 | 3.442 | 1.179 | 2.92 | 0.005 | 1.078 | 5.806 |
| 盗塁刺 | -6.9517 | 2.714 | -2.561 | 0.013 | -12.396 | -1.508 |
| 併殺打 | 0.3204 | 0.938 | 0.342 | 0.734 | -1.561 | 2.202 |
| 失策 | 10.3099 | 3.953 | 2.608 | 0.012 | 2.381 | 18.239 |
| OPS | -39.7195 | 41.192 | -0.964 | 0.339 | -122.34 | 42.901 |
| PF | -87.9498 | 66.615 | -1.32 | 0.192 | -221.562 | 45.663 |
最後に分析が正しいかどうかダーウィンワトソン比に熱視線！
| Omnibus: | 77.134 | Durbin-Watson: | 1.781 |
|---|---|---|---|
| Prob(Omnibus): | 0 | Jarque-Bera (JB): | 849.409 |
| Skew: | 2.853 | Prob(JB): | 3.57E-185 |
| Kurtosis: | 18.126 | Cond. No. | 5.45E+04 |
Durbin-Watson: 1.781
２に近いほど、信頼できるとされているが、もうちょいがんばろか、、、
さてさて、ここで改めて予測と推定年俸を見比べる。
Salary_Central_ATBATcsv.ipynb
import matplotlib.pyplot as plt
import japanize_matplotlib
pred = result.predict(X)
df['予測'] = pred
df.plot.bar(y=['年俸\n 百万円','予測'], x='選手',rot=(60),figsize=(60,5), title='Adj. R-squared（修正決定係数）:0.693')
#VIF
おまけですが、多重共線性を避けるために、その説明変数を除外するかしないか考えたときに参考になる指標として、分散拡大係数(VIF：Variance Inflation Factor)というものがあります。一般的にVIFの値が10(公式のリファレンスでは、5)を超えると、依存関係が強いため、適切な重回帰分析ができないと言われています。
Salary_Central_ATBATcsv.ipynb
from statsmodels.stats.outliers_influence import variance_inflation_factor as vif
num_cols = model.exog.shape[1] # 説明変数の列数
vifs = [vif(model.exog, i) for i in range(0, num_cols)]
pd.DataFrame(vifs, index=model.exog_names, columns=['VIF'])
| VIF | |
|---|---|
| const | 1.018245e+02 |
| wRAA | 2.128536e+04 |
| wRC | 8.794399e+03 |
| wRC+ | 4.634665e+00 |
| 試合 | 4.101142e+01 |
| 打席 | 4.920061e+07 |
| 打数 | 3.730298e+07 |
| 得点 | 2.368701e+02 |
| 二塁打 | 4.250410e+02 |
| 三塁打 | 2.809364e+01 |
| 本塁打 | 1.168782e+03 |
| 塁打 | 1.872602e+05 |
| 打点 | 3.293852e+02 |
| 三振 | 5.054945e+01 |
| 四球 | 5.962007e+05 |
| 敬遠 | 1.883050e+01 |
| 死球 | 8.371199e+03 |
| 犠打 | 3.624088e+04 |
| 犠飛 | 2.456959e+03 |
| 盗塁 | 8.083278e+01 |
| 盗塁刺 | 5.446593e+01 |
| 併殺打 | 2.359446e+01 |
| 失策 | 3.290462e+02 |
| OPS | 1.489067e+00 |
| PF | 1.441706e+00 |
#最後に
重回帰分析というと、教師データを８割、テストデータを２割に分割して、それぞれ決定係数を比較するものですが、「statsmodels」は、分割せず分析している事例しか見たことがないので、もし間違った認識であれば、ご意見ご感想をお寄せ下さい。
今回のデータ元は、「BASEBALL LAB」と「NPB公式ホームページ」に基づいて、最新の野球統計であるセイバーメトリクスを参考にしながら、選手ごとに通算成績を独自に算出し、重回帰分析（主にOLS)を「google colabratory」にて実装したものであリます。
今回の結果をさらに精度を上げるには、ゴロ率、フライ率、得点創出能力といった説明変数を増やす作業や、散布図を使って、多重共線性を避ける努力をしないといけません。
守備能力も追加すべきところです。
ここまでお時間を作っていただき厚く御礼申し上げます。これからもパリーグの野手、投手でもさらに充実した分析を行いますので、まだまだ勉強不足ではございますが、ご声援下さい。ご支援下さい。