概要

野球の攻撃にはいろいろな能力が求められます。例えばボールを遠くに飛ばしたり早い打球を打つための「パワー」、バットをボールに当てるための「ミート力」、次の塁に進塁するための「走力」など様々な能力が必要になります。

今回は各選手の能力を明らかにすべく、2018年のプロ野球（セ･パ両リーグ）の打者のデータから因子分析を行いたいと思います。
そして最後に因子分析から明らかになった能力それぞれのTOP5を発表します！！

また、pythonでは因子分析をする際にいくつかの方法があるようですが、今回はsklearnを使用したいと思います。他には僕の知る限りでは「factor_analyzer」を利用する方法もあるようです。

環境

google colab

因子分析とは

たくさんの結果（変数）の背後に潜んでいる要因を明らかにすることです。例えば、とある因子が盗塁数と二塁打、三塁打の影響を受けている場合、これらの背後に潜んでいる要因は「足の速さ」であると考えられ、この因子は「走力」であると定義できます。

準備

グラフを作るときに日本語に対応できるように「japanize-matplotlib」をインストールします。これがなかなか便利です！


!pip install japanize-matplotlib

次に必要なライブラリをインポートしていきます！


import os
import pandas as pd
import numpy as np
import scipy.stats as stats
from time import sleep

import matplotlib.pyplot as plt
import seaborn as sns
import japanize_matplotlib
%matplotlib inline
%config InlineBackend.figure_formats = {'png', 'retina'}


import warnings
warnings.filterwarnings('ignore')

pd.options.display.max_columns = 500
pd.options.display.max_rows = 100

データの取得

html_list()を使ってデータを所得していきます。


html_list = ["h", "l", "m", "e", "bs", "f", "g", "t", "c", "db", "d", "s"]

df_list = []
for i in html_list:
    lst = pd.read_html(f"http://xxx.jp/xx/2018/xxxxx/xxxxxx_{i}.html", flavor="bs4")
    df_list.append(lst[0])
    sleep(3)

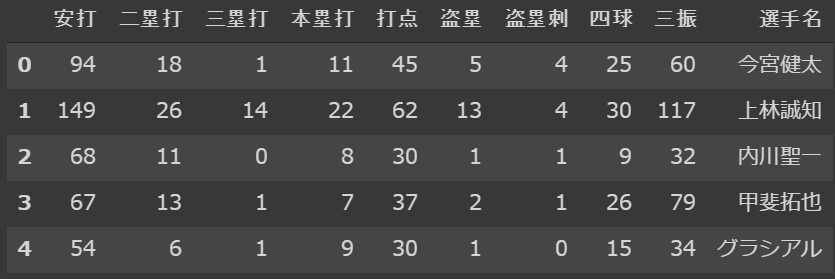
データはこんな感じで取得しています。このままでは扱いにくいので、データを整形していきます。

データの整形


b_data = pd.concat(df_list, ignore_index=True) # ひとつのデータフレームにします。
b_data = b_data[b_data[0] != "* 左打　+ 左右打"] # 不要な情報なので除去

for i in range(len(b_data.columns)):
    b_data[i] = b_data[i].str.replace("　", "") # 全角のスペースを除去

b_data = b_data.reset_index(drop = True)
b_data = b_data.drop(0,axis=1) 
b_data.columns = b_data.loc[0] # カラム置き換え
b_data = b_data.drop(0,axis=0)
b_data = b_data[b_data["選手"] != "選手"] # 不要な情報なので除去
b_data = b_data.reset_index(drop = True)
b_data_int = b_data.iloc[:,1:19].astype(int) # 分析するために型をintへ変換
b_data_float = b_data.iloc[:,20:22].astype(float) # 分析するために型をfloatへ変換
b_data_c = pd.concat([b_data_int, b_data_float], axis=1)
b_data_c["選手名"] = b_data["選手"]
b_data_c = b_data_c.reset_index(drop=True)

分析の条件

すべての打者を含めてしまうと打席数の少ない選手が多く偏りが出てしまいます。今回スクレイピングした選手は総勢666選手。この中には投手や打席数が極端に少ない選手も含まれています。なので、ある程度打席に立っている選手にするため、今回は200打席以上とします。

# 200打席以上
b_data_con = b_data_c[b_data_c["打席"] >= 200]
b_data_con = b_data_con.reset_index(drop=True)

変数選択

今回の分析に必要と思われる変数のみに絞りたいと思います。基準は一打席における成績に関係しそうなものと盗塁に関係するものとしています。犠飛や犠打については状況による影響も大きいと判断して除外しました。

data_select = b_data_con.iloc[:,[4, 5, 6, 7, 9, 10, 11, 14, 17, 20]]

一塁打の算出と打数補正

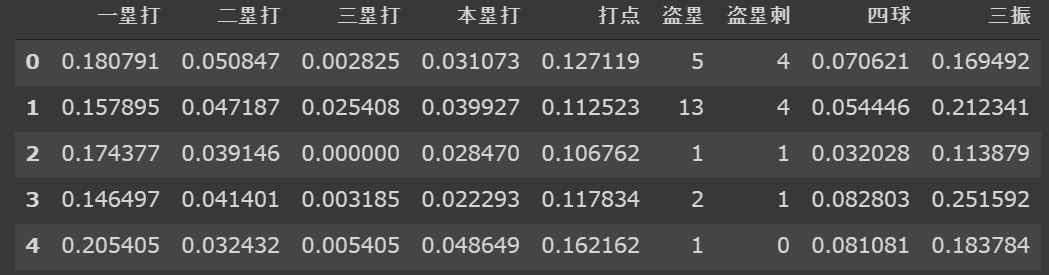
今回スクレイピングしたデータの中には「一塁打」が存在しません。そのため、安打と二塁打、三塁打、本塁打から一塁打を算出したいと思います。
また、各選手の打数が異なるため、一塁打、二塁打、三塁打、本塁打、三振については打数で割り、それぞれ、打数における率を算出したいと思います。


data_select["一塁打"] = (data_select["安打"] - data_select["二塁打"] - data_select["三塁打"] - data_select["本塁打"]) / b_data_con["打数"]
data_select["二塁打"] = data_select["二塁打"] / b_data_con["打数"]
data_select["三塁打"] = data_select["三塁打"] / b_data_con["打数"]
data_select["本塁打"] = data_select["本塁打"] / b_data_con["打数"]
data_select["打点"] = data_select["打点"] / b_data_con["打数"]
data_select["四球"] = data_select["四球"] / b_data_con["打数"]
data_select["三振"] = data_select["三振"] / b_data_con["打数"]

data_s = data_select.iloc[:,[10, 1, 2, 3, 4, 5, 6, 7, 8]]

相関を確認

相関を確認して、いくつの因子に分けるかを決めたいと思います。

plt.figure(figsize=(10, 10))
sns.heatmap(data_pre_s.corr(method = "spearman"),
                square=True, vmax=1, vmin=-1, center=0, annot=True, cmap='RdBu_r')

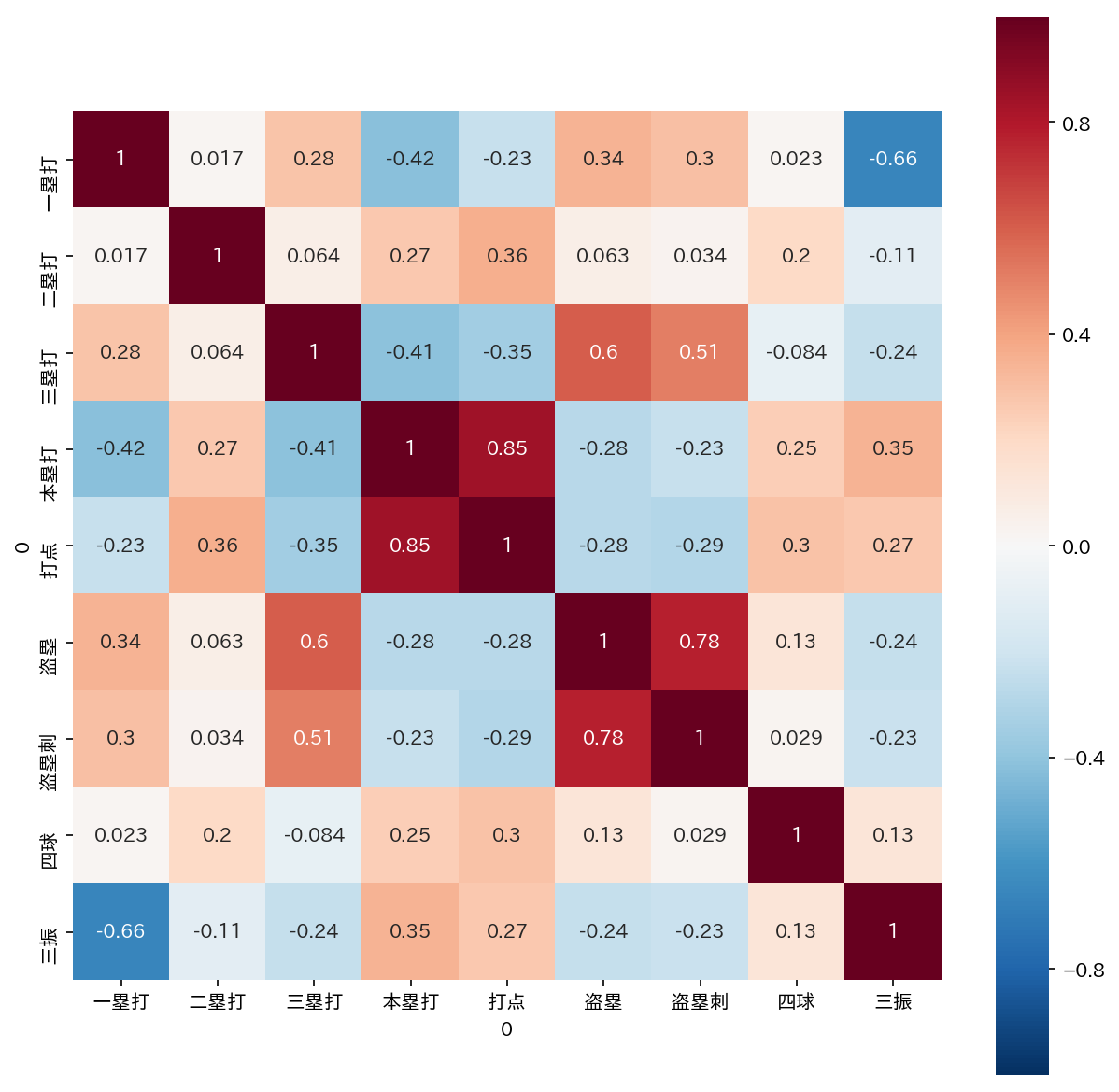
見た感じだと

一塁打と三振に負の相関
三塁打と盗塁、三塁打と盗塁刺、盗塁と盗塁刺にそれぞれ正の相関
本塁打と打点に正の相関

といった感じの3つの因子に分けられそうだなと判断します。というわけで今回は3つの因子で分析を進めたいと思います。

標準化


sc = StandardScaler()
data_std = pd.DataFrame(sc.fit_transform(data_s))

因子分析：sklearnを使用

ここから因子分析開始です！

from sklearn.decomposition import FactorAnalysis as FA
# 共通因子の数
fa = FA(n_components=3, max_iter=5000)
X_fa = fa.fit_transform(data_std)

はい、終わり。

因子負荷量を確認

それぞれの因子について、どの変数の影響が大きいかを確認していきます！

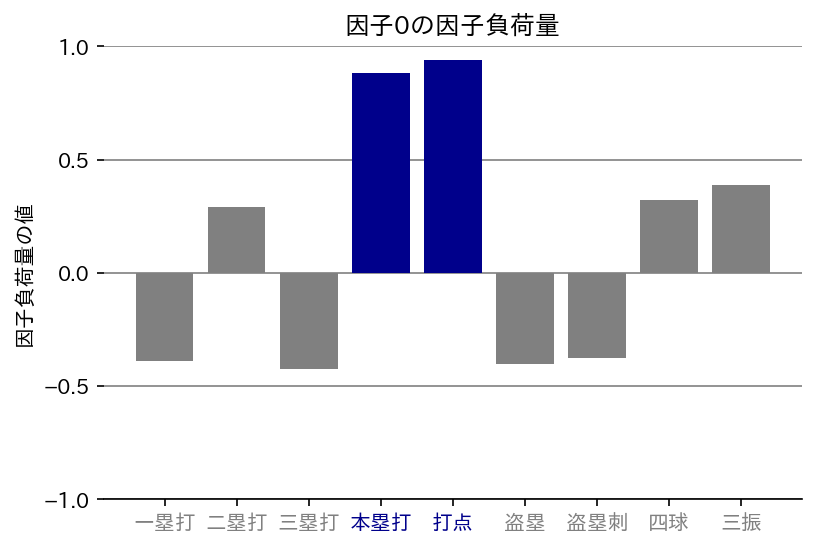
因子0

colorlist= ['grey', 'grey', 'grey', 'darkblue', 'darkblue', 'grey', 'grey', 'grey', 'grey']

plt.figure(1)     
ax = plt.subplot(111)
ax.bar(data_s.columns, (fa.components_[0]), color=colorlist) #ベクトルのプラスマイナスを変換
ax.set_xticks(data_s.columns)
ax.set_xticklabels(data_s.columns, rotation=270)
ax.set_yticks([-1, -0.5, 0, 0.5, 1])
ax.set_title('因子0の因子負荷量')
ax.set_ylabel('因子負荷量の値')
plt.ylim([-1, 1])
plt.xticks(rotation = '0')
#plt.hlines(y=[0], xmin=-1, xmax=4, colors='grey', linestyles='solid', linewidths=1)
plt.grid(axis = "y", color='grey')
plt.rcParams['axes.axisbelow'] = True
plt.gca().spines['right'].set_visible(False)
plt.gca().spines['left'].set_visible(False)
plt.gca().spines['top'].set_visible(False)

for xtick, color in zip(ax.get_xticklabels(), colorlist):
    xtick.set_color(color)

本塁打と打点が大きな値を示しています。これらの背後に潜んでいる要因といえば、「パワー」ですね。打点の解釈が難しいですが、こちらとこちらを参考にしたいと思います。

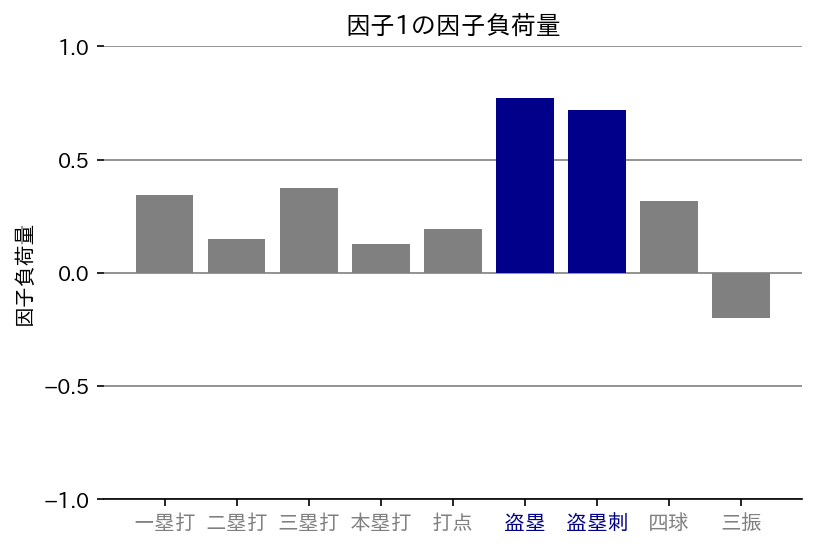
因子1

colorlist= ['grey', 'grey', 'grey', 'grey', 'grey', 'darkblue', 'darkblue', 'grey', 'grey']

plt.figure(1)     
ax = plt.subplot(111)
ax.bar(data_s.columns, (fa.components_[1]), color=colorlist) #ベクトルのプラスマイナスを変換
ax.set_xticks(data_s.columns)
ax.set_xticklabels(data_s.columns, rotation=270)
ax.set_yticks([-1, -0.5, 0, 0.5, 1])
ax.set_title('因子1の因子負荷量')
ax.set_ylabel('因子負荷量')
plt.ylim([-1, 1])
plt.xticks(rotation = '0')
#plt.hlines(y=[0], xmin=-1, xmax=4, colors='grey', linestyles='solid', linewidths=1)
plt.grid(axis = "y", color='grey')
plt.rcParams['axes.axisbelow'] = True
plt.gca().spines['right'].set_visible(False)
plt.gca().spines['left'].set_visible(False)
plt.gca().spines['top'].set_visible(False)

for xtick, color in zip(ax.get_xticklabels(), colorlist):
    xtick.set_color(color)

盗塁、盗塁刺の因子負荷量が大きい値を示していますね。盗塁刺に関しても足が速くなければ盗塁を企てることもないでしょう。ということで因子1は「走力」としたいと思います。

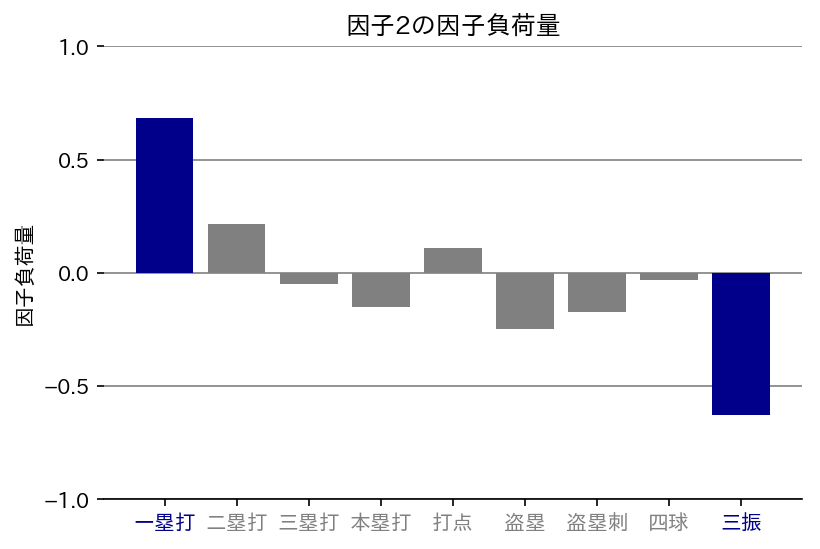
因子2

colorlist= ['darkblue', 'grey', 'grey', 'grey', 'grey', 'grey', 'grey', 'grey', 'darkblue']

plt.figure(1)     
ax = plt.subplot(111)
ax.bar(data_s.columns, (fa.components_[2]), color=colorlist) #ベクトルのプラスマイナスを変換
ax.set_xticks(data_s.columns)
ax.set_xticklabels(data_s.columns, rotation=270)
ax.set_yticks([-1, -0.5, 0, 0.5, 1])
ax.set_title('因子2の因子負荷量')
ax.set_ylabel('因子負荷量')
plt.ylim([-1, 1])
plt.xticks(rotation = '0')
#plt.hlines(y=[0], xmin=-1, xmax=4, colors='grey', linestyles='solid', linewidths=1)
plt.grid(axis = "y", color='grey')
plt.rcParams['axes.axisbelow'] = True
plt.gca().spines['right'].set_visible(False)
plt.gca().spines['left'].set_visible(False)
plt.gca().spines['top'].set_visible(False)

for xtick, color in zip(ax.get_xticklabels(), colorlist):
    xtick.set_color(color)

一塁打が大きな値を示している、三振が低い値を示しているということでこれは「ミート力」ですね！わかりやすい！

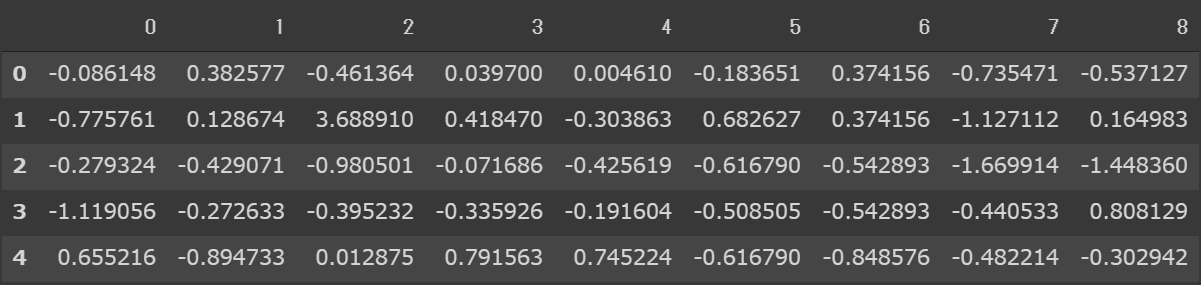
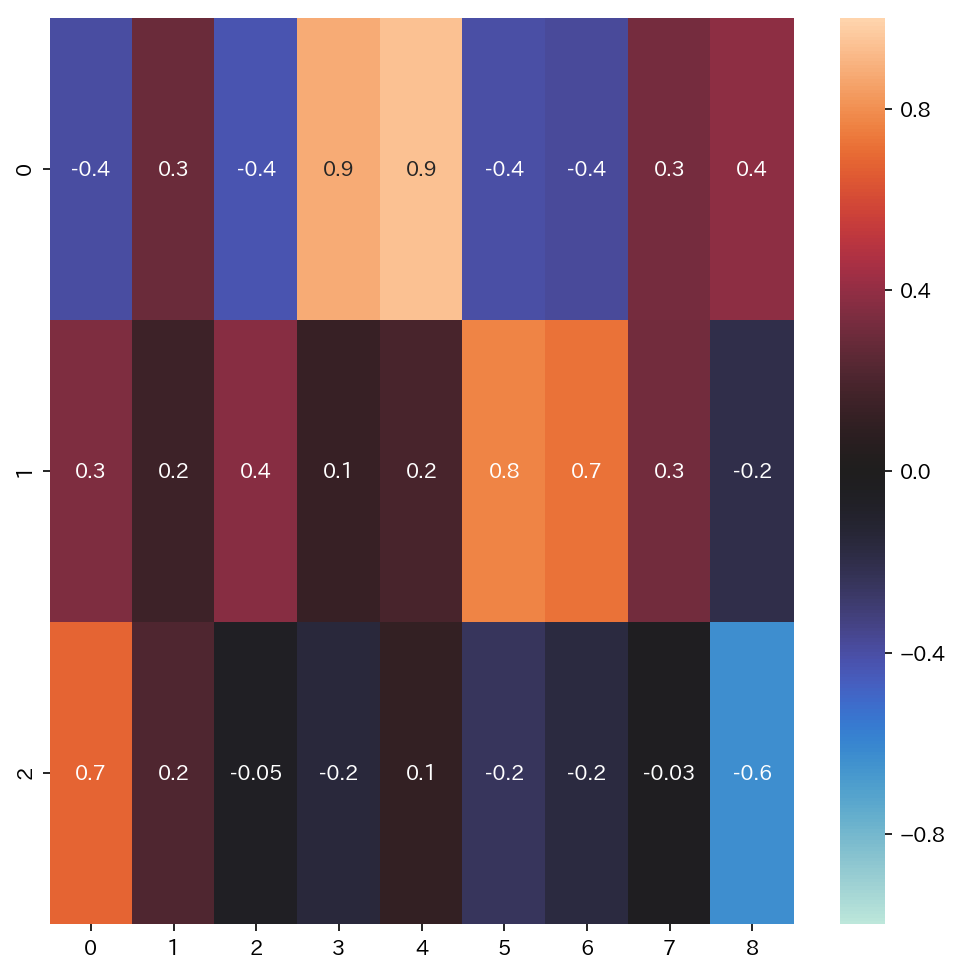
ヒートマップ

ちなみに、ヒートマップで確認したい場合はこんな感じです。

plt.figure(figsize=(8, 8))
sns.heatmap(pd.DataFrame(fa.components_), vmax=1, vmin=-1, center=0, annot=True, fmt='.1g')

因子得点

各選手に因子得点を算出していきたいと思います。

result = pd.DataFrame(X_fa)
result.columns = ['パワー', '走力','ミート力']
result = pd.concat([result, data_select.iloc[:, [9, 10, 1, 2, 3, 4, 5, 6, 7, 8]]], axis=1)

TOP5

それぞれの因子得点の高いTOP5を発表します！！

パワー

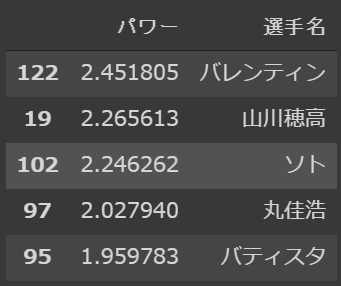
result[["パワー","選手名"]].sort_values(by = 'パワー', ascending=False).head()

第一位はバレンティン選手です。第二位は山川選手、その後はソト選手、丸選手、バティスタ選手と続きます。パワーがありそうな選手が並びましたね。広島からは丸選手とバティスタ選手の2選手がはいりました。

走力


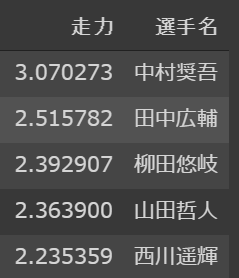
result[["走力","選手名"]].sort_values(by = '走力', ascending=False).head()

第一位は中村選手です。第二位は田中選手、その後は柳田選手、山田選手、西川選手と続きます。盗塁数や盗塁を多く企画する選手が並びました！中村選手は走力の値がひとり飛びぬけていますね。

ミート力

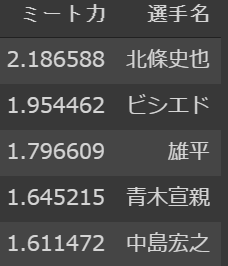
result[["ミート力","選手名"]].sort_values(by = 'ミート力', ascending=False).head()

第一位は北條選手です。第二位はビシエド選手、その後は雄平選手、青木選手、中島選手と続きます。三振の少なそうな選手が出てきましたね。

まとめ

今回は因子分析を用いて、各選手のホームランと打点の多い「パワー」、一塁打が多く三振の少ない「ミート力」、盗塁と盗塁刺の多い「走力」の3つの能力の値を算出しました。因子分析では解釈が難しいこともあるかと思いますが、今回は比較的綺麗にできたと思います。しかし、これらはあくまで試合における成績であり、試合の状況においてホームランを狙える場面や盗塁を企画できる場面に遭遇した数も影響することを考慮する必要があります。

因子分析でプロ野球選手の能力を明らかにしてみた

概要

環境